NLineIntegrate

NLineIntegrate[f,{x,y,…}∈curve]

computes the numerical scalar line integral of the function f[x,y,…] over the curve.

NLineIntegrate[{p,q,…},{x,y,…}∈curve]

computes the numerical vector line integral of the vector function {p[x,y,…],q[x,y,…],…}.

Details and Options

  • Line integrals are also known as curve integrals and work integrals.
  • Scalar line integrals integrate scalar functions along a curve. They typically compute things like length, mass and charge for a curve.
  • Vector line integrals are used to compute the work done by a vector function along a curve in the direction of its tangent. Typical vector functions include a force field, electric field and fluid velocity field.
  • The scalar line integral of the function f along a curve 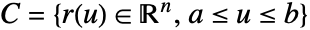is given by:
  • … where TemplateBox[{{{r, ^, {(, ', )}}, (, u, )}}, Norm] is the measure of a parametric curve segment.
  • The scalar line integral is independent of the parametrization and orientation of the curve. Any one-dimensional RegionQ object can be used as a curve.
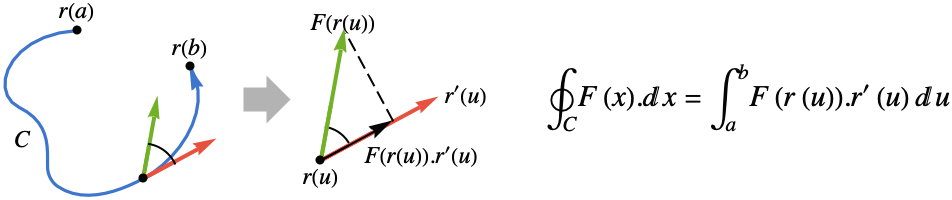
  • The vector line integral of the function F along a curve 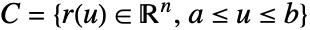is given by:
  • … where 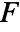F(r(u)).r^(')(u) is projection of the vector function 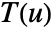onto the tangent direction so only the component in the tangent direction gets integrated.
  • The vector line integral is independent of the parametrization of the curve, but it does depend on the orientation of the curve.
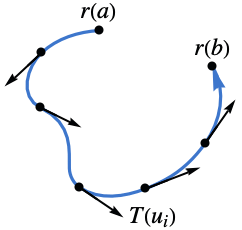
  • The orientation for a curve is given by a tangent vector field 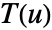over the curve.
  • For a parametric curve ParametricRegion[{r1[u],…,rn[u]},…], the tangent vector field 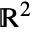is taken to be ∂ur[u].
  • Special curves in with their assumed tangent orientations include:
  • Line[{p1,p2,…}]the orientation follows the points in the order they are given from p1 to p2 etc.
    HalfLine[{p1,p2}]
    HalfLine[p,v]    		the orientation is from p1 to p2 or in the v direction
    InfiniteLine[{p1,p2}]
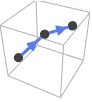
    InfiniteLine[p,v]    		the orientation is from p1 to p2 or in the v direction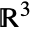
    Circle[p,r]the orientation is counterclockwise
  • Special curves in with their assumed tangent orientations include:
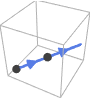
  • Line[{p1,p2,…}]the orientation follows the points in the order they are given from p1 to p2 etc.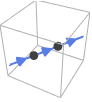
    HalfLine[{p1,p2}]
    HalfLine[p,v]    		the orientation is from p1 to p2 or in the v direction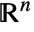
    InfiniteLine[{p1,p2}]
    InfiniteLine[p,v]    		the orientation is from p1 to p2 or in the v direction
  • Special curves in 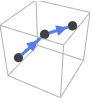with their assumed tangent orientations include:
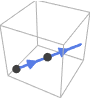
  • Line[{p1,p2,…}]the orientation follows the points in the order they are given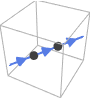
    HalfLine[{p1,p2}]
    HalfLine[p,v]    		the orientation is from p1 to p2 the orientation is given by v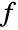
    InfiniteLine[{p1,p2}]
    InfiniteLine[p,v]    		the orientation is from p1 to p2 the orientation is given by v
  • The following options can be given:
  • AccuracyGoal Infinitydigits of absolute accuracy sought
    MaxPoints Automaticmaximum total number of sample points
    MaxRecursion Automaticmaximum number of recursive subdivisions
    Method Automaticmethod to use
    MinRecursion 0minimum number of recursive subdivisions
    PrecisionGoal Automaticdigits of precision sought
    WorkingPrecision MachinePrecisionthe precision used in internal computations

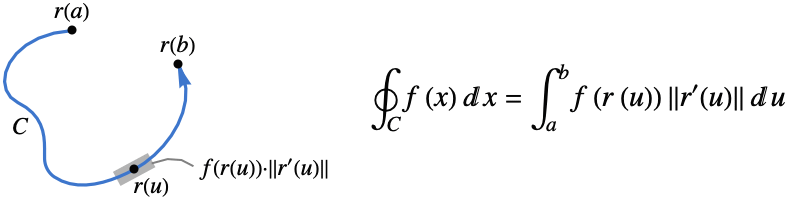
Examples

open allclose all

Basic Examples  (6)

Line integral of a scalar field over a circle:

Line integral of a vector field over a line segment:

Line integral of a vector field over a space curve:

Line integral of a scalar field in two dimensions:

Curve over which to integrate:

A contour plot of and the curve:

The line integral:

Line integral of a vector field in two dimensions:

The vector field and the integration path:

The line integral:

Line integral of a vector field in three dimensions:

Scope  (33)

Basic Uses  (4)

Line integral of a scalar field:

Line integral of a vector field in three dimensions:

LineIntegrate works with many special curves:

Line integral over a parametric curve:

Scalar Functions  (11)

Line integral of a scalar field over a curve:

Contour plot of and the curve:

Line integral:

Line integral of a scalar field over an arc of a circle:

Line integral of a scalar field over a parametric curve:

Contour plot of the function and the curve:

Line integral of a scalar field over a circle:

Line integral of a scalar field over a space curve:

Line integral:

Line integral of a scalar field over the boundary of an annulus:

Contour plot of the function and the curve:

Line integral of a scalar field over a closed polygon:

Contour plot of the function and the curve:

Line integral of a scalar field over an elliptical path:

Contour plot of the function and the curve:

Line integral:

Line integral of a scalar field over a parametric curve:

Line integral:

Line integral of a scalar field over a circle:

Contour plot of and the curve:

Line integral:

Line integral of a scalar field over the boundary of a sector of a disk:

Contour plot of and the curve:

Line integral:

Vector Functions  (12)

Line integral of a vector field in three dimensions over a parametrized curve:

Visualization of the vector field and the curve:

Line integral:

Line integral of a vector field over a curve in two dimensions:

Line integral:

Line integral of a vector field over a circular arc:

Line integral of a vector field over a line segment:

Line integral of a vector field over a parametrized curve in three dimensions:

Line integral of a vector field over a curve:

Line integral of a vector field over an elliptical arc:

Line integral of a vector field over a parametric curve:

Line integral of a vector field over a parametric curve in three dimensions:

Line integral of a vector field over a parametrized curve:

Line integral of a vector field over an elliptical path:

Line integral of a vector field in higher dimensions:

Special Curves  (4)

Line integral over a circular arc:

Line integral of a vector field over the boundary of a circular sector of radius 1:

Line integral over a polygon:

Line integral over the boundary of an annulus:

Parametric Curves  (2)

Line integral of a vector field over a spiral in three dimensions:

Line integral of a scalar field over a parametric curve:

Options  (8)

AccuracyGoal  (1)

The option AccuracyGoal sets the number of digits of accuracy:

The result with default settings only sets a PrecisionGoal:

MaxPoints  (1)

The option MaxPoints stops the integration after a specified number of points has been evaluated:

With default options:

MaxRecursion  (1)

The option MaxRecursion specifies the maximum number of recursive steps:

Increasing the number of recursions:

The exact result is:

Method  (1)

The option Method can take the same values as in NIntegrate. For example:

With the default option:

Compare to the truncated exact result:

MinRecursion  (1)

The option MinRecursion forces a minimum number of subdivisions:

Compare to the exact result:

PrecisionGoal  (1)

The option PrecisionGoal sets the relative tolerance in the integration:

With default settings:

WorkingPrecision  (2)

If a WorkingPrecision is specified, the computation is done at that working precision:

The result has finite precision if the integrand has a finite precision:

Applications  (27)

College Calculus  (10)

Line integral of a function over a line segment:

Line integral of a vector field over a curve:

Mass of a thin circular wire of radius 1 with linear density :

Work done by the force field on a particle that moves along a line segment:

Line integral of a vector field along a path:

Line integral of a vector field along a curve:

Work done by the force as a particle moves along the curve :

Line integral of a vector field along the unit circle centered at the origin:

Line integral of a vector field along a circle of radius 2 centered at the origin:

Numerical value of the line integral of a vector field over a path:

Lengths  (3)

Circumference of a circle:

Perimeter of a cardioid using a line integral:

The length can also be calculated with RegionMeasure:

Perimeter of an astroid:

Areas  (5)

Area of an ellipse with semiaxes of length 2 and 3, calculated using a line integral:

Area of the right-hand loop of the lemniscate computed using a line integral:

Area of the epicycloid of parameters and :

Area of the cardioid using a line integral:

Area of an astroid using a line integral:

Work by a Force  (4)

Work done by a force force as an object is moved on a straight line:

Work done by the electric force as a charged particle of charge is moved from {1,1,0} to {2,2,0} in the electric field of a charged infinite wire of charge density :

Work done by an elastic force directed toward the origin as a quarter of an ellipse is traced:

Work of the electric force as a charge is moved along the axis from to infinity in the electric field of a charge :

Centroids  (2)

Mass of a closed semicircular wire of radius 2 and unit linear density:

coordinate of the center of mass:

coordinate of the center of mass:

Moments of inertia of a helix-shaped wire of unit linear density:

About the axis:

About the axis:

About the axis:

Classical Theorems  (3)

A vector field is conservative if its line integral depends only on the values at the endpoints, not on the path:

The field is the gradient of a scalar function :

All gradients of scalar fields are conservative. For example, the line integral of over the curve is:

This is the same as the difference of the values of at the endpoints of the curve:

Green's theorem. The line integral of the vector field over a closed curve is:

This can be related to a surface integral of over the region enclosed by the curve, where is defined as:

Stokes's theorem. The line integral of a vector field along a closed line in three dimensions is:

This is equal to the surface integral of the Curl of on any surface having the curve as its boundary:

The surface integral across a different surface with the same boundary is the same:

Properties & Relations  (5)

Apply N[LineIntegrate[…]] to obtain a numerical solution if the symbolic calculation fails:

Find the center of mass of a triangular wire of unit linear density:

Find the total mass:

Find the component of the center of mass:

Find the component:

The center of mass can also be obtained using RegionCentroid:

Find the moment of inertia around the axis of a circular wire of unit linear density centered at the origin in the - plane:

The answer can also be computed with MomentOfInertia:

Find the length of an epicycloid:

The same answer can be obtained using ArcLength:

Find the area of an ellipse:

The result can be obtained using RegionMeasure:

Neat Examples  (2)

Length of a catenary:

Integral of a vector field over a Clelia curve:

Wolfram Research (2024), NLineIntegrate, Wolfram Language function, https://reference.wolfram.com/language/ref/NLineIntegrate.html.

Text

Wolfram Research (2024), NLineIntegrate, Wolfram Language function, https://reference.wolfram.com/language/ref/NLineIntegrate.html.

CMS

Wolfram Language. 2024. "NLineIntegrate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NLineIntegrate.html.

APA

Wolfram Language. (2024). NLineIntegrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NLineIntegrate.html

BibTeX

@misc{reference.wolfram_2024_nlineintegrate, author="Wolfram Research", title="{NLineIntegrate}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/NLineIntegrate.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_nlineintegrate, organization={Wolfram Research}, title={NLineIntegrate}, year={2024}, url={https://reference.wolfram.com/language/ref/NLineIntegrate.html}, note=[Accessed: 21-November-2024 ]}