ContourIntegrate[f,z∈cont]
gives the integral of f along the contour defined by cont in the complex plane.






ContourIntegrate
ContourIntegrate[f,z∈cont]
gives the integral of f along the contour defined by cont in the complex plane.
Details and Options




- Contour integration is also known as path integration or complex line integration.
- Contour integrals arose in the study of holomorphic and meromorphic functions in complex analysis, but they are now used in a wide range of applications, including the computation of inverse Laplace transforms and Z transforms, definite integrals and sums, and solutions of partial differential equations.
- The contour integral of a function
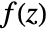 along a contour cont
along a contour cont 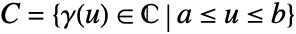 is given by:
is given by: - The value of the contour integral is independent of the parametrization, but it does depend on the orientation of the contour cont.
- The function f is typically a meromorphic function of z, but it can be any piecewise continuous function that is defined in a neighborhood of cont in the complex plane.
- The contour integral of a meromorphic function
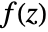 along a closed contour cont can be computed using Cauchy's residue theorem.
along a closed contour cont can be computed using Cauchy's residue theorem. - Commonly used closed contours cont include: »
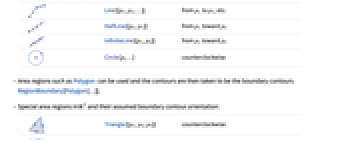
-

{"Hairpin", hl} encircle a half-line hl 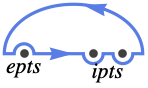
{"UpperSemicircle",ipts,epts} encircle the upper half-plane, including the points ipts and excluding the points epts, all on the real axis 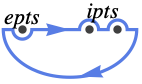
{"LowerSemicircle",ipts,epts} encircle the lower half-plane, including the points ipts and excluding the points epts, all on the real axis 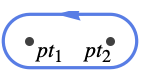
{"Dumbbell",pt1,pt2} encircle the capsule given by points pt1 and pt2 - The complex points are given as {x,y} pairs; complex half-lines are given as HalfLine primitives.
- A contour cont in
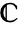 can also be specified as a curve region (RegionQ) in
can also be specified as a curve region (RegionQ) in  .
. - For a parametric contour ParametricRegion[{x[t],y[t]},{{t,a,b}}], the orientation is in the direction of increasing t.
- Special contours in
 and their assumed orientation:
and their assumed orientation: -

Line[{p1,p2,…}] from p1 to p2, etc. 
HalfLine[{p1,p1}] from p1 toward p2 
InfiniteLine[{p1,p2}] from p1 toward p2 
Circle[p,…] counterclockwise - Area regions such as Polygon can be used and the contours are then taken to be the boundary contours RegionBoundary[Polygon[…]].
- Special area regions in
 and their assumed boundary contour orientation:
and their assumed boundary contour orientation: -

Triangle[{p1,p2,p3}] counterclockwise 
Rectangle[p1,p2] counterclockwise 
RegularPolygon[n,…] counterclockwise 
Polygon[{p1,p2,…}{{q1,q2,…},…}] counterclockwise of the outer contour, clockwise for inner contours 
Disk[p,…] counterclockwise 
Ellipsoid[p,…] counterclockwise 
StadiumShape[{p1,p2},r] counterclockwise 
Annulus[p,{rm,rm},…] counterclockwise for outer contour and clockwise for inner contour - ContourIntegrate uses a combination of symbolic and numerical methods when the input involves inexact quantities.
- The regions in cont may be wrapped with Inactive to prevent autoevaluation.
- The following options can be given:
-
Assumptions $Assumptions assumptions to make about parameters GenerateConditions Automatic whether to generate answers that involve conditions on parameters PrincipalValue False whether to find Cauchy principal values WorkingPrecision Automatic the precision used in internal computations
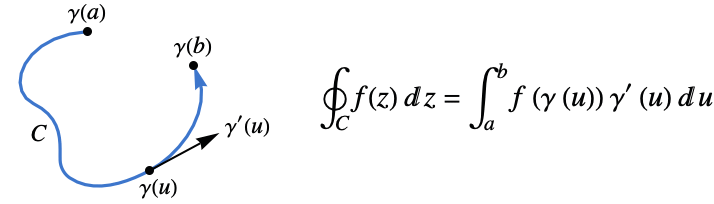
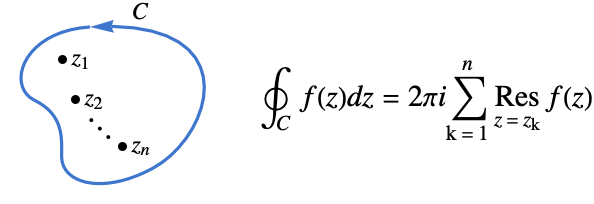
Examples
open all close allBasic Examples (3)
Scope (53)
Basic Uses (5)
Special Topic: Rational Functions (13)
Integrate a rational function along a circle:
Integrate a parametric rational function along a circle:
Integrate a rational function along a pentagonal contour:
Contour integral of a rational function along a triangular path:
Contour integral of a rational function along a rectangular path:
Contour integral along the unit circle:
Contour integral over an open polygonal chain:
Contour integral over an open arc:
Contour integral of a meromorphic function over a closed semicircle:
Contour integral of a function with an essential singularity:
Contour integral of a non-analytic function:
Contour integral of a function containing a branch cut:
Contour integral of a function depending on a symbolic parameter:
Special Topic: Meromorphic Functions (5)
Special Topic: Functions with Essential Singularities (4)
Sin function with an essential singularity inside the contour:
Contour integral of a function with an essential singularity:
Special Topic: Non-analytic Functions (4)
Contour integral over a circular path:
Contour integral of the Arg function:
Special Topic: Functions with Branch Cuts (2)
Special Topic: Symbolic Parameters (5)
Function and contour can contain symbolic parameters:
Suppress conditions of existence using GenerateConditions False:
Result is a Piecewise function:
Contour integral along a half-disk of radius ![]() :
:
Special Topic: Named Contours (8)
Contour integral along the real axis in positive direction, around poles on the real axis, closing in the upper half of the complex plane:
Contour integral along the real axis in positive direction, around poles on the real axis, closing in the lower half of the complex plane:
By default, this contour is traversed clockwise.
Contour integral around a hairpin or Hankel contour:
Integral around a hairpin or Hankel contour:
Contour integral that evaluates to a Zeta function:
Special Topic: Region Contours (7)
Options (6)
Assumptions (1)
The option Assumptions can be used on parameters:
GenerateConditions (2)
ContourIntegrate generates conditions on parameters with GenerateConditionsAutomatic:
Use the option GenerateConditionsFalse to suppress the existence conditions:
Generate conditions when the contour involves parameters:
Suppress the conditions using GenerateConditionsFalse:
PrincipalValue (1)
The option PrincipalValue can be used to calculate the Cauchy principal value:
WorkingPrecision (2)
When WorkingPrecision is set, the integral is evaluated numerically:
If the input has a finite precision, the integral is evaluated numerically:
Applications (22)
Rational Functions (2)
Contour integral on a half-disk:
The same result obtained with Integrate:
Trig-Rational Products (2)
Trigonometric Functions (3)
Fourier Transform (2)
Inverse Laplace Transform (4)
Inverse Laplace transform of a function:
Computation using a contour integral:
Inverse Laplace transform of a rational function:
Inverse Laplace transform of a function containing a square root:
The same computation using a contour integral:
Inverse Laplace transform of a function containing Log:
Inverse Mellin Transform (4)
Inverse Z Transform (2)
Classical Theorems (3)
Residue theorem applied to the contour integral of a meromorphic function over a closed path:
The integral is equal to ![]() times the sum of the residues of the poles inside the contour:
times the sum of the residues of the poles inside the contour:
The integration contour can be deformed without changing the value of the integral, provided that no singularities of the function are crossed:
If no singularities lie inside the contour, the integral is zero:
Properties & Relations (6)
Apply N[ContourIntegrate[...]] to obtain a numerical solution if the symbolic calculation fails:
This can also be computed using NIntegrate:
Contour integrals can also be obtained using Integrate:
Integrate can integrate along a straight contour in the complex plane:
Contour integrals over a closed path can also be obtained using ResidueSum:
Poles of a meromorphic function can be found using FunctionPoles:
The integral can also be computed using Residue:
Contour integrals over a closed path can also be obtained using Residue:
Interactive Examples (2)
Related Guides
History
Text
Wolfram Research (2023), ContourIntegrate, Wolfram Language function, https://reference.wolfram.com/language/ref/ContourIntegrate.html.
CMS
Wolfram Language. 2023. "ContourIntegrate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ContourIntegrate.html.
APA
Wolfram Language. (2023). ContourIntegrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ContourIntegrate.html
BibTeX
@misc{reference.wolfram_2025_contourintegrate, author="Wolfram Research", title="{ContourIntegrate}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/ContourIntegrate.html}", note=[Accessed: 06-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_contourintegrate, organization={Wolfram Research}, title={ContourIntegrate}, year={2023}, url={https://reference.wolfram.com/language/ref/ContourIntegrate.html}, note=[Accessed: 06-January-2026]}