LineIntegrate[f,{x,y,…}∈curve]
computes the scalar line integral of the function f[x,y,…] over the curve.
LineIntegrate[{p,q,…},{x,y,…}∈curve]
computes the vector line integral of the vector function {p[x,y,…],q[x,y,…],…}.


LineIntegrate
LineIntegrate[f,{x,y,…}∈curve]
computes the scalar line integral of the function f[x,y,…] over the curve.
LineIntegrate[{p,q,…},{x,y,…}∈curve]
computes the vector line integral of the vector function {p[x,y,…],q[x,y,…],…}.
Details and Options





- Line integrals are also known as curve integrals and work integrals.
- Scalar line integrals integrate scalar function along a curve. They typically compute things like length, mass and charge for a curve.
- Vector line integrals are used to compute the work done by a vector function as it moves along a curve in the direction of its tangent. Typical vector functions include a force field, electric field and fluid velocity field.
- The scalar line integral of the function f along a curve
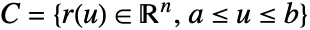 is given by:
is given by: - where
![TemplateBox[{{{r, ^, {(, ', )}}, (, u, )}}, Norm] TemplateBox[{{{r, ^, {(, ', )}}, (, u, )}}, Norm]](Files/LineIntegrate.en/4.png) is the measure of a parametric curve segment.
is the measure of a parametric curve segment. - The scalar line integral is independent of the parametrization and orientation of the curve. Any one dimensional RegionQ object can be used as curve.
- The vector line integral of the function F along a curve
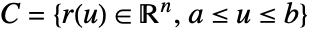 is given by:
is given by: - where
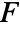 is projection of the vector function
is projection of the vector function 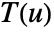 onto the tangent direction so only the component in the tangent direction gets integrated.
onto the tangent direction so only the component in the tangent direction gets integrated. - The vector line integral is independent of the parametrization of the curve, but it does depend on the orientation of the curve.
- The orientation for a curve is given by a tangent vector field
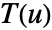 over the curve.
over the curve. - For a parametric curve ParametricRegion[{r1[u],…,rn[u]},…], the tangent vector field
 is taken to be ∂ur[u].
is taken to be ∂ur[u]. - Special curves in
 with their assumed tangent orientation include:
with their assumed tangent orientation include: -

Line[{p1,p2,…}] the orientation follows the points in the order they are given from p1 to p2 etc. 
HalfLine[{p1,p2}]
HalfLine[p,v]the orientation is from p1 to p2 or in the v direction 
InfiniteLine[{p1,p2}]
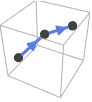
InfiniteLine[p,v]the orientation is from p1 to p2 or in the v direction 
Circle[p,r] the orientation is counterclockwise - Special curves in
 with their assumed tangent orientation include:
with their assumed tangent orientation include: -
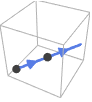
Line[{p1,p2,…}] the orientation follows the points in the order they are given from p1 to p2 etc. 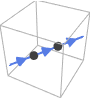
HalfLine[{p1,p2}]
HalfLine[p,v]the orientation is from p1 to p2 or in the v direction 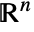
InfiniteLine[{p1,p2}]
InfiniteLine[p,v]the orientation is from p1 to p2 or in the v direction - Special curves in
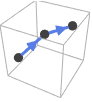 with their assumed tangent orientation include:
with their assumed tangent orientation include: -
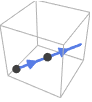
Line[{p1,p2,…}] the orientation follows the points in the order they are given 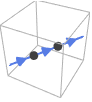
HalfLine[{p1,p2}]
HalfLine[p,v]the orientation is from p1 to p2 the orientation is given by v 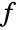
InfiniteLine[{p1,p2}]
InfiniteLine[p,v]the orientation is from p1 to p2 the orientation is given by v - The coordinates along the curve can be specified using VectorSymbol. »
- The following options can be given:
-
Assumptions $Assumptions assumptions to make about parameters Direction Automatic orientation of the curve GenerateConditions Automatic whether to generate answers that involve conditions on parameters WorkingPrecision Automatic the precision used in internal computations - LineIntegrate uses a combination of symbolic and numerical methods when the input involves inexact quantities.



Examples
open all close allBasic Examples (7)
Line integral of a scalar field over a circle:
Line integral of a vector field over a line segment:
Line integral of a vector field over a space curve:
Line integral of a scalar field in two dimensions:
Curve over which to integrate:
A contour plot of ![]() and the curve:
and the curve:
Line integral of a vector field in two dimensions:
The vector field and the integration path:
Line integral of a vector field in three dimensions:
Use VectorSymbol:
Scope (32)
Basic Uses (4)
Scalar Functions (11)
Line integral of a scalar field over a curve:
Contour plot of ![]() and the curve:
and the curve:
Line integral of a scalar field over an arc of a circle:
Line integral of a scalar field over a parametric curve:
Contour plot of the function and the curve:
Line integral of a scalar field over a circle:
Line integral of a scalar field over a space curve:
Line integral of a scalar field over the boundary of an annulus:
Contour plot of the function and the curve:
Line integral of a scalar field over a closed polygon:
Contour plot of the function and the curve:
Line integral of a scalar field over an elliptical path:
Contour plot of the function and the curve:
Line integral of a scalar field over a parametric curve:
Line integral of a scalar field over a circle:
Contour plot of ![]() and the curve:
and the curve:
Line integral of a scalar field over the boundary of a sector of a disk:
Vector Functions (12)
Line integral of a vector field in three dimensions over a parametrized curve:
Visualization of the vector field and the curve:
Line integral of a vector field over a curve in two dimensions:
Line integral of a vector field over a circular arc:
Line integral of a vector field over a line segment:
Line integral of a vector field over a parametrized curve in three dimensions:
Line integral of a vector field over a curve:
Line integral of a vector field over an elliptical arc:
Line integral of a vector field over a parametric curve:
Line integral of a vector field over a parametric curve in three dimensions:
Line integral of a vector field over a parametrized curve:
Special Curves (4)
Options (5)
Assumptions (1)
The option Assumptions can be used on parameters:
Direction (1)
GenerateConditions (1)
LineIntegrate can work with symbolic parameters:
WorkingPrecision (2)
If a WorkingPrecision is specified, a numerical result is given:
The result has finite precision if the integrand has a finite precision:
Applications (27)
College Calculus (10)
Line integral of a function ![]() over a line segment:
over a line segment:
Line integral of a vector field over a curve:
Mass of a thin circular wire of radius 1 with linear density ![]() :
:
Work done by the force field ![]() on a particle that moves along a line segment:
on a particle that moves along a line segment:
Line integral of a vector field along a path:
Line integral of a vector field along a curve:
Work done by the force ![]() as a particle moves along the curve
as a particle moves along the curve ![]() :
:
Line integral of a vector field along the unit circle centered at the origin:
Line integral of a vector field along a circle of radius ![]() centered at the origin:
centered at the origin:
Numerical value of the line integral of a vector field over a path:
Lengths (3)
Perimeter of a cardioid using a line integral:
The length can also be calculated with RegionMeasure:
Areas (5)
Work by a Force (4)
Work done by the gravitational force as an object is moved on a straight line:
Work done by the electric force as a charge ![]() is moved from {1,1,0} to {2,2,0} in the electric field of a charged infinite wire of charge density
is moved from {1,1,0} to {2,2,0} in the electric field of a charged infinite wire of charge density ![]() :
:
Work done by an elastic force directed toward the origin as a quarter of an ellipse is traced:
Work of the electric force as a charge ![]() is moved along the
is moved along the ![]() axis from
axis from ![]() to infinity in the electric field of a charge
to infinity in the electric field of a charge ![]() :
:
Centroids (2)
Classical Theorems (3)
A vector field is conservative if its line integral depends only on the values at the endpoints, not on the path:
The field ![]() is the gradient of a scalar function
is the gradient of a scalar function ![]() :
:
All gradients of scalar fields are conservative. For example, the line integral of ![]() over the curve is:
over the curve is:
This is the same as the difference of the values of ![]() at the endpoints of the curve:
at the endpoints of the curve:
The line integral of the vector field ![]() over a closed curve is:
over a closed curve is:
This can be related to a surface integral of ![]() over the region enclosed by the curve, where
over the region enclosed by the curve, where ![]() is defined as:
is defined as:
The line integral of a vector field ![]() along a closed line in three dimensions is:
along a closed line in three dimensions is:
This is equal to the surface integral of the Curl of ![]() on any surface having the curve as its boundary:
on any surface having the curve as its boundary:
The surface integral across a different surface with the same boundary is the same:
Properties & Relations (5)
Apply N[LineIntegrate[...]] to obtain a numerical solution if the symbolic calculation fails:
Find the center of mass of a triangular wire of unit linear density:
Find the ![]() component of the center of mass:
component of the center of mass:
The center of mass can also be obtained using RegionCentroid:
Find the moment of inertia around the ![]() -axis of a circular wire of unit linear density centered at the origin in the
-axis of a circular wire of unit linear density centered at the origin in the ![]() -
-![]() plane:
plane:
The answer can also be computed with MomentOfInertia:
Find the length of an epicycloid:
The same answer can be obtained using ArcLength:
The result can be obtained using RegionMeasure:
Related Guides
Text
Wolfram Research (2023), LineIntegrate, Wolfram Language function, https://reference.wolfram.com/language/ref/LineIntegrate.html (updated 2025).
CMS
Wolfram Language. 2023. "LineIntegrate." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/LineIntegrate.html.
APA
Wolfram Language. (2023). LineIntegrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LineIntegrate.html
BibTeX
@misc{reference.wolfram_2025_lineintegrate, author="Wolfram Research", title="{LineIntegrate}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/LineIntegrate.html}", note=[Accessed: 04-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_lineintegrate, organization={Wolfram Research}, title={LineIntegrate}, year={2025}, url={https://reference.wolfram.com/language/ref/LineIntegrate.html}, note=[Accessed: 04-January-2026]}