NLineIntegrate

NLineIntegrate[f,{x,y,…}∈curve]

関数 f[x,y,…]の curve 上の数値スカラー線積分を計算する．

NLineIntegrate[{p,q,…},{x,y,…}∈curve]

ベクトル関数{p[x,y,…],q[x,y,…],…}の数値ベクトル線積分を計算する．

詳細とオプション

  • 線積分は曲線積分または仕事積分としても知られている．
  • スカラー線積分は，スカラー関数を曲線に沿って積分する．これは，通常，曲線の長さ，質量，電荷等の積分に使われる．
  • ベクトル線積分は，ベクトル関数の接線の向きの曲線に沿った仕事量の計算に使われる．典型的なベクトル関数には力場，電場，流体速度場等が含まれる．
  • 関数 f の curve 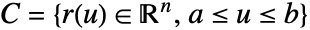に沿ったスカラー線積分は以下で与えられる．
  • ただし，TemplateBox[{{{r, ^, {(, ', )}}, (, u, )}}, Norm]はパラメトリック曲線の線分の測度値である．
  • スカラー線積分は curve のパラメータ化や方向には依存しない．任意の一次元RegionQオブジェクトを curve として使うことができる．
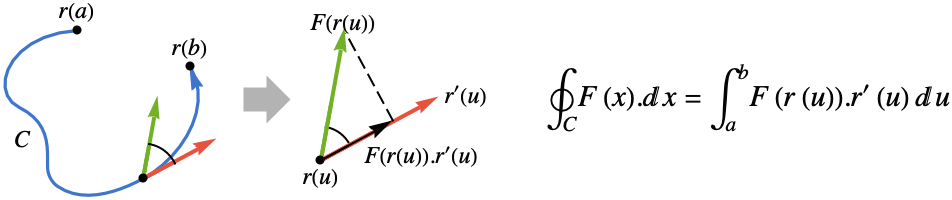
  • 関数 F の曲線 curve 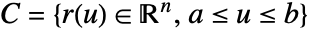に沿ったベクトル線積分は以下で与えられる．
  • ただし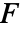，F(r(u)).r^(')(u) はベクトル関数 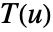の接線方向への投影であるので，接線方向の成分しか積分されない．
  • ベクトル線積分は，曲線のパラメータ化には依存しないが，曲線の向きには依存する．
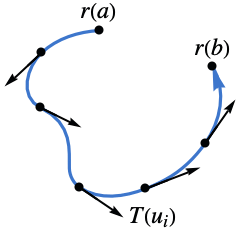
  • 曲線の方向は曲線上の接線ベクトル場 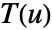によって与えられる．
  • パラメトリック曲線ParametricRegion[{r1[u],…,rn[u]},…]については，接線ベクトル場 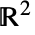は ∂ur[u]であるとみなされる．
  • 次は，における特殊曲線とその仮定される接線の方向である．
  • Line[{p1,p2,…}]方向は与えられる点の順に従う（例： p1からp2まで）
    HalfLine[{p1,p2}]
    HalfLine[p,v]    		v 方向または p1から p2まで
    InfiniteLine[{p1,p2}]
    InfiniteLine[p,v]    		v 方向または p1から p2まで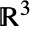
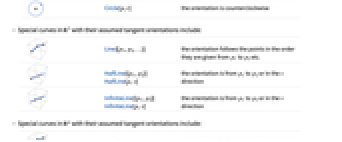
    Circle[p,r]方向は反時計回り
  • 次は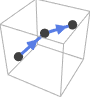，における特殊曲線とその仮定される接線の方向である．
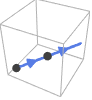
  • Line[{p1,p2,…}]方向は与えられる点の順に従う（例： p1からp2まで）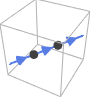
    HalfLine[{p1,p2}]
    HalfLine[p,v]    		v 方向または p1から p2まで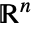
    InfiniteLine[{p1,p2}]
    InfiniteLine[p,v]    		v 方向または p1から p2まで
  • 次は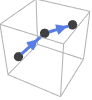，における特殊曲線とその仮定される接線の方向である．
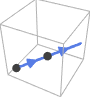
  • Line[{p1,p2,…}]方向は与えられる点の順に従う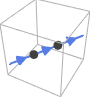
    HalfLine[{p1,p2}]
    HalfLine[p,v]    		方向は p1からo p2まで 方向は v で与えられる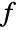
    InfiniteLine[{p1,p2}]
    InfiniteLine[p,v]    		方向は p1からo p2まで 方向は v で与えられる
  • 次は，使用可能なオプションである．
  • AccuracyGoal Infinity目的確度の桁数
    MaxPoints Automaticサンプル点の最大合計数
    MaxRecursion Automatic再帰的下位区分の最大数
    Method Automatic使用するメソッド
    MinRecursion 0再帰的下位区分の最小数
    PrecisionGoal Automatic目標精度の桁数
    WorkingPrecision MachinePrecision内部計算精度

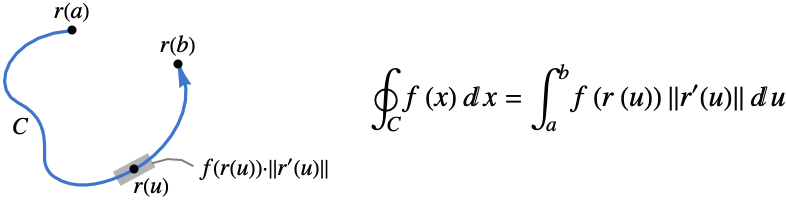
例題

すべて開くすべて閉じる

例  (6)

円上のスカラー場の線積分：

線分上のベクトル場の線積分：

空間曲線上のベクトル場の線積分：

スカラー場の二次元における線積分：

その上で積分する曲線：

と曲線の等高線プロット：

線積分：

二次元におけるベクトル場の線積分：

ベクトル場と積分路：

線積分：

三次元におけるベクトル場の線積分：

スコープ  (33)

基本的な用法  (4)

スカラー場の線積分：

三次元におけるベクトル場の線積分：

LineIntegrateは多くの特殊曲線に使うことができる：

パラメトリック曲線上の線積分：

スカラー関数  (11)

曲線上のスカラー場の線積分：

と曲線の等高線プロット：

線積分：

円の円弧上のスカラー場の線積分：

パラメトリック曲線上のスカラー場の線積分：

関数と曲線の等高線プロット：

スカラー場の曲線上の線積分：

スカラー場の空間曲線上の線積分：

線積分：

スカラー場のアニュラスの境界上の線積分：

関数と曲線の等高線プロット：

スカラー場の閉じた多角形上の線積分：

関数と曲線の等高線プロット：

スカラー場の楕円経路上の線積分：

関数と曲線の等高線プロット：

線積分：

スカラー場のパラメトリック曲線上の線積分：

線積分：

スカラー場の円上の線積分：

と曲線の等高線プロット：

線積分：

スカラー場の円板の扇形上の線積分：

と曲線の等高線プロット：

線積分：

ベクトル関数  (12)

三次元におけるベクトル場のパラメータ曲線上の線積分：

ベクトル場と曲線の可視化：

線積分：

二次元におけるベクトル場の曲線上の線積分：

線積分：

ベクトル場の円の円弧上の線積分：

ベクトル場の線分上の線積分：

三次元におけるベクトル場のパラメータ曲線上の線積分：

ベクトル場の曲線上の線積分：

ベクトル場の楕円の円弧上の線積分：

ベクトル場のパラメータ曲線上の線積分：

三次元におけるベクトル場のパラメータ曲線上の線積分：

ベクトル場のパラメータ曲線上の線積分：

ベクトル場の楕円経路上の線積分：

ベクトル場のより高次元における線積分：

特殊曲線  (4)

円の円弧上の線積分：

ベクトル場の半径1の円形扇形の境界上の線積分：

多角形上の線積分：

アニュラスの境界上の線積分：

パラメトリック曲線  (2)

ベクトル場の三次元における螺旋上の線積分：

スカラー場のパラメトリック曲線上の線積分：

オプション  (8)

AccuracyGoal  (1)

オプションAccuracyGoalは確度の桁数を設定する：

デフォルト設定による結果はPrecisionGoalしか設定しない：

MaxPoints  (1)

オプションMaxPointsは，指定数の点の評価を終えると積分を停止する：

デフォルトオプションでは以下のようになる：

MaxRecursion  (1)

オプションMinRecursionは再帰ステップの最大数を指定する：

再帰回数を増やす：

厳密な結果は以下のようになる：

Method  (1)

オプションMethodはNIntegrateにおけるのと同じ値を取る．以下の例を見よ：

デフォルトオプションでは以下のようになる：

切り取った厳密な結果と比較する：

MinRecursion  (1)

オプションMinRecursionを使うと強制的に下位区分の数が最低になる：

厳密な結果と比較する：

PrecisionGoal  (1)

オプションPrecisionGoalは積分における相対許容度を設定する：

デフォルト設定では以下のようになる：

WorkingPrecision  (2)

WorkingPrecisionが指定されていると，計算はその作業精度で行われる：

被積分関数の精度が有限なとき，結果は有限精度になる：

アプリケーション  (27)

大学の微積分  (10)

関数 の線分上の線積分：

ベクトル場の曲線上の線積分：

線形密度が で半径1の細い円形ワイヤの質量：

線分に沿って動く粒子に対する力場 の仕事量：

ベクトル場の経路に沿った線積分：

ベクトル場の曲線に沿った線積分：

粒子が曲線 に沿って動く際の力 による仕事量：

原点を中心とする単位円に沿ったベクトル場の線積分：

原点を中心とする半径2の円に沿ったベクトル場の線積分：

経路に沿ったベクトル場の線積分の数値：

長さ  (3)

円の円周：

線積分を使ったカージオイドの外周：

長さはRegionMeasureを使っても計算できる：

星芒形の外周：

面積  (5)

線積分で計算した，半軸の長さが2と3の楕円の面積：

線積分で計算した，レムニスケート の右側ループの面積：

パラメータが で の外サイクロイドの面積：

線積分によるカージオイドの面積：

線積分による星芒形の面積：

力の仕事  (4)

物体が直線上を移動するときの力 によって行われる仕事：

電荷 の荷電粒子が電荷密度 の荷電無限ワイヤの電場内で{1,1,0}から{2,2,0}に移動するときに電気力によって行われる仕事：

楕円の4分の1が追跡された場合に原点に向かう弾性力によって行われる仕事：

電荷 の電場で，電荷 が 軸に沿って から無限大まで移動するときの電気力の仕事：

重心  (2)

半径2で単位線形密度の閉じた半円ワイヤの質量：

質量の中心の 座標：

質量の中心の 座標：

単位線形密度の螺旋状のワイヤの慣性モーメント：

軸について：

軸について：

軸について：

古典的な定理  (3)

ベクトル場は，その線積分が経路上の値ではなく端点の値にのみ依存する場合は「保存的」である：

場 はスカラー関数 の勾配である：

スカラー場の勾配はすべて保存的である．例えば，曲線上の の線積分は以下のようになる：

これは，曲線の端点における の値の差と等しい：

グリーン(Green)の定理によると，閉じた曲線上のベクトル場 の線積分は以下のようになる：

これは，曲線に囲まれた領域における の面積分と関連付けることができる． は以下のように定義される：

ストークス(Stokes)の定理によると，三次元における閉じた線に沿ったベクトル場 の線積分は以下のようになる：

これは，曲線を境界として持つ任意の曲面状の のCurlの面積分に等しい：

同じ境界を持つ異なる曲面に渡る面積分は等しい：

特性と関係  (5)

記号計算ができない場合はN[LineIntegrate[…]]を適用して数値解を得る：

単位線形密度の三角形のワイヤの質量の中心を求める：

質量の合計を求める：

質量の中心の 成分を求める：

成分を求める：

質量の中心はRegionCentroidを使って求めることもできる：

- 平面上で原点を中心とし，単位線密度を持つ円形ワイヤの 軸の周りの慣性モーメントを求める：

答はMomentOfInertiaで計算することもできる：

外サイクロイドの長さを求める：

同じ答はArcLengthを使って求めることもできる：

楕円の面積を求める：

結果はRegionMeasureで求めることができる：

おもしろい例題  (2)

懸垂線の長さ：

ベクトル場のClelia曲線上の線積分：

Wolfram Research (2024), NLineIntegrate, Wolfram言語関数， https://reference.wolfram.com/language/ref/NLineIntegrate.html.

テキスト

Wolfram Research (2024), NLineIntegrate, Wolfram言語関数， https://reference.wolfram.com/language/ref/NLineIntegrate.html.

CMS

Wolfram Language. 2024. "NLineIntegrate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NLineIntegrate.html.

APA

Wolfram Language. (2024). NLineIntegrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NLineIntegrate.html

BibTeX

@misc{reference.wolfram_2024_nlineintegrate, author="Wolfram Research", title="{NLineIntegrate}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/NLineIntegrate.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_nlineintegrate, organization={Wolfram Research}, title={NLineIntegrate}, year={2024}, url={https://reference.wolfram.com/language/ref/NLineIntegrate.html}, note=[Accessed: 21-November-2024 ]}