NMaxValue

NMaxValue[f,x]

x についての f の最大値を与える．

NMaxValue[f,{x,y,…}]

x, y, …についての f の最大値を与える．

NMaxValue[{f,cons},{x,y,…}]

制約条件 cons に従った f の最大値を与える．

NMaxValue[…,x∈reg]

x が領域 reg 内にあるように制限する．

詳細とオプション

  • NMaxValueは大域的最適化(GO)としても知られている．
  • NMaxValueは，与えられた制約条件に従って常に f の最大値を求めようとする．
  • NMaxValueは，通常，制約が与えられた場合に可能な最大値を求めるために使われる．分野によっては，最適な戦略，最良適合，最適な構成等と呼ばれることがある．
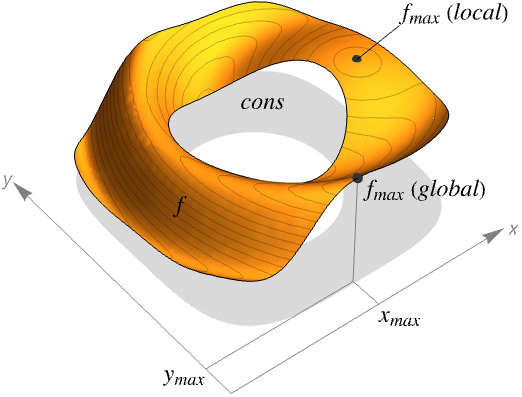
  • f が線形または凹で cons が線形または凸のとき，NMaxValueが与える結果は実数および整数値の両方の上で最大値になる．それ以外の場合は結果が単に極大値であるかもしれない．
  • NMaxValueが制約条件を満足できないと判断した場合は-Infinityが返される．
  • NMaxValueは，目的関数 f と制約条件 cons がスカラー変数またはベクトル変数に依存する式で与えられるモデリング言語をサポートする．f と cons は，一般に，非常に効率的な形に解析されるが，f と cons の項が変数の数値に対して数値を与える限りNMaxValueはしばしば解を求めることができる．
  • 制約条件 cons は以下の論理結合でよい．
  • lhs==rhs等式
    lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhs不等式 (LessEqual, …)
    lhsrhs, lhsrhs, lhsrhs, lhsrhsベクトル不等式 (VectorLessEqual, …)
    {x,y,…}∈rdom領域指定
  • NMaxValue[{f,cons},x∈rdom]は，事実上，NMaxValue[{f,cons&&x∈rdom},x]に等しい．
  • x∈rdom については，Indexed[x,i]を使って別の座標に言及することができる．
  • 次は，使用可能な領域 rdom である．
  • Reals実数スカラー変数
    Integers整数スカラー変数
    Vectors[n,dom]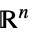のベクトル変数
    Matrices[{m,n},dom]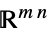の行列変数
    ℛ幾何学領域 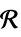に制限されたベクトル変数
  • デフォルトで，変数はすべて実数であるとみなされる．
  • 次は，指定可能なオプションである．
  • AccuracyGoalAutomatic目標となる最終確度桁数
    EvaluationMonitor Nonef が評価されたときに常に評価される式
    MaxIterationsAutomatic使用する最大反復回数
    Method Automatic使用されるメソッド
    PrecisionGoalAutomatic目標となる最終精度桁数
    StepMonitor Noneステップを取るたびに常に評価される式
    WorkingPrecision MachinePrecision内部計算に使用する精度
  • AccuracyGoalとPrecisionGoalの設定で，最大値の位置の値と最大になったときの関数の値の両方で目標とする桁数を指定する．
  • NMaxValueは，AccuracyGoalとPrecisionGoalで指定された目標値のどちらかが達成されるまで計算を続ける．
  • NMaxValueのためのメソッドには2つのクラスがある．最初のクラスは問題の特性を使うので，メソッドが収束する際に求まった最大値は大域的であることが保証される．2番目のクラスは発見的なメソッドで，複数の局所探索を使うことがあるが，一般的には確率論によって調整され，大域的最大値に焦点が当てられる．このメソッドもしばしば大域的な最大値を求めるが，必ずそうするとは保証されない．
  • 次は，解に収束する場合に最大値を与えることが保証されているメソッドである．
  • "Convex"凸法だけを使う
    "MOSEK"凸問題用の商用MOSEKライブラリを使う
    "Gurobi"凸問題用の商用Gurobiライブラリを使う
    "Xpress"凸問題用の商用Xpressライブラリを使う
  • 次は，発見的な方法である．
  • "NelderMead"Nelder・Meadのシンプレックス法
    "DifferentialEvolution"差分進化を使う
    "SimulatedAnnealing"焼きなまし法を使う
    "RandomSearch"複数のランダムな初期点から始めて求まった最良の極小値を使う
    "Couenne"非凸混合整数非線形問題にCouenneライブラリを使う

例題

すべて開くすべて閉じる

例  (5)

一変数関数の最大値を求める：

多変数関数の最大値を求める：

制約条件に従って関数の最大値を求める：

幾何学領域上で関数の最大値を求める：

幾何学領域上で関数の最大値を求める：

スコープ  (34)

基本的な用法  (12)

制約条件 に従って を最大化する：

いくつかの線形不等式制約はVectorGreaterEqualで表現できる：

v>= または\[VectorGreaterEqual]を使ってベクトル不等式の記号を入力する：

スカラー不等式を使った同等の形：

ベクトル変数 を使う：

にスレッディングの可能性があるので，不等式 は とは等しくないかもしれない：

での意図しないスレッディングを避けたければInactive[Plus]を使うとよい：

定数パラメータを持つ方程式を使って での意図しないスレッディングを回避する：

VectorGreaterEqualは"NonNegativeCone"についての錐不等式を表す：

円錐の次元を明示的に指定したければ，{"NonNegativeCone",n}を使うとよい：

解を求める：

制約条件 に従って を最大化する：

"NormCone"で錐不等式を使って制約条件 を指定する：

解を求める：

制約条件 に従って関数 を最大化する：

Indexedを使ってベクトル変数の成分（例：TemplateBox[{x, 1}, IndexedDefault]）にアクセスする：

ベクトル変数の次元と領域が曖昧なときはVectors[n,dom]を使って指定する：

NonNegativeReals (TemplateBox[{}, NonNegativeReals])を使って非負の制約条件を指定する：

ベクトル不等式 を使った同等の形：

NonPositiveReals (TemplateBox[{}, NonPositiveReals])を使って非正の制約条件を指定する：

ベクトル不等式を使った同等の形：

Orという制約を指定することができる：

領域制約1  (4)

Integersを使って整数領域の制約を指定する：

Vectors[n,Integers]を使ってベクトル変数に整数領域の制約を指定する：

NonNegativeIntegers (TemplateBox[{}, NonNegativeIntegers])を使って非負の整数領域の制約を指定する：

NonPositiveIntegers (TemplateBox[{}, NonPositiveIntegers])を使って非正の整数領域の制約を指定する：

領域制約2  (3)

の におけるベクトルの線形関数の最大値を求める，ただし，TemplateBox[{x}, Norm]<=1：

領域上の最大値を求める：

異なる2つの領域内にあるように制約されている2点間の可能な最大距離を求める：

線形問題  (5)

線形の目的関数と制約条件がある場合は，最大値が見付かるとそれは大域的になる：

制約条件は等式制約および不等式制約である：

Equalを使っていくつかの等式制約を一度に表現する：

いくつかのスカラー等式を使った同等の形：

VectorLessEqualを使っていくつかのLessEqual不等式制約を一度に表現する：

v<= を使ってベクトル不等式をコンパクトな形で入力する：

スカラー不等式を使った同等の形：

Intervalを使って変数の境界を指定する：

凸問題  (4)

"NonNegativeCone"を使って の形の線形関数を指定する：

v>= を使ってベクトル不等式をコンパクトな形で入力する：

凸二次制約条件に従って凹二次関数の最大値を求める：

領域をプロットする：

が半正定値になるようなの最大値を求める：

目的関数のプロットを示す：

が半正定値でとなるような凹目的関数の最大値を求める：

領域と最大化点をプロットする：

凸に変換可能  (3)

不等式制約とノルム制約に従って擬似凹関数 を最大化する．目的関数は2つの非負のアフィン関数の積なので，擬似凹関数である：

最大化は負の目的関数（擬似凹関数）を最小化することで解くことができる．擬似凹問題はパラメータ についてのパラメトリック凸最適化問題として解くことができる：

目的関数を等位集合 の関数としてプロットする：

区間内の等位集合の値について，最小の目的関数が求まる：

等位集合の値が大きくなると，問題は実行不可能になる：

制約条件に従って を最大にする．目的関数は凸関数ではないが凸関数の差 として表すことができる．ただし， と は凸関数である：

領域と最小化点をプロットする：

制約条件に従って を最大にする．制約条件のは凸ではないが，凸条件の差 で表すことができる．ただし， と は凸関数である：

領域と最小化点をプロットする：

一般的な問題  (3)

非線形制約条件に従って線形目的関数を最大化する：

プロットする：

非線形目的関数を線形制約条件に従って最大化する：

目的関数と最大化点をプロットする：

非線形目的関数を非線形制約条件に従って最大化する：

プロットする：

オプション  (7)

AccuracyGoalとPrecisionGoal  (2)

次で，収束基準とを強制する：

次で，収束基準とを強制する．これはデフォルトの機械精度計算では達成できない：

WorkingPrecisionの設定値を高くするとプロセスが収束するようになる：

EvaluationMonitor  (1)

関数の解を求める過程で評価したすべての点を最小値の環で記録する：

訪れた点の中で目的関数の値で最終的な解に近いすべての点をプロットする：

Method  (2)

メソッドの中には特定の問題に対して準最適な結果を与えるものがある：

この問題の場合は，自動選択されたメソッドが最適な結果を与える：

この非凸問題に対して自動メソッド選択は"Couenne"を選ぶ：

目的関数を最大値とともにプロットする：

速度を求めるなら，たくさんの変数がある問題には"NelderMead"メソッドを使う：

StepMonitor  (1)

NMaxValueが関数の最大値を求めるのに取るステップ：

WorkingPrecision  (1)

作業精度をにする．デフォルトでAccuracyGoalとPrecisionGoalはに設定されている：

アプリケーション  (4)

幾何学の問題  (2)

三角形と楕円が交差する範囲内の の最大値を求める：

結果の領域を求める：

の正方形内に収まる 個の重なり合ない円の最大半径 とその中心を求める．ボックス制約は として表すことができる：

円は重なってはならない：

変数を集める：

最大半径 を求める：

投資問題  (1)

投資収益率が最大となるように，資本金250,000ドルを2つの株と1つの債権に割り当てる方法を求める．2つの株への投資額を ，債権への投資額を とする：

電気・ガス株に投資される金額は40,000ドルを超えることはできない：

債権に投資される金額は最低でも70,000ドルでなければならない：

2つの株への投資総額は全投資額の少なくとも半分でなければならない：

株式からはそれぞれ9％と4％の年間配当が支払われる．債権は5%の配当がある．投資の全収益は以下の通りである：

株式と債権の購入および取引実行のための費用はであり，1000ドルを超えてはならない：

指定の制約条件内で達成可能な最大利益は以下の通りである：

反復最適化  (1)

の最大値が最小となるような，楕円 に関連付けられたパラメータ の値を求める：

距離を の関数として示す：

目的関数の最大値を最小にする最適パラメータ を求める：

特性と関係  (7)

NMaximizeは最大値と，変数の値を最大にする規則を与える：

NArgMaxは最大化する値のリストを与える：

NMaxValueは最大値だけを与える：

関数 f の最大化は-f の最小化に等しい：

凸問題については，ConvexOptimizationを使って追加的な解の特性が得られるかもしれない：

双対解を得る：

パラメータがある凸問題について，ParametricConvexOptimizationを使うとParametricFunctionが与えられる：

ParametricFunctionはパラメータの値について評価できる：

NMaxValueを使ってパラメトリック問題についての関数を定義する：

2通りのアプローチの所要時間を比較する：

ParametricFunctionの導関数も計算できる：

RobustConvexOptimizationは，パラメータ制約がある凸問題についてはパラメータの可能なすべての値について有効な最適値を求める：

NMaxValueはパラメータの特定の値についてより大きい最大値を求めるかもしれない：

この値を与えるマキシマイザは と の使用可能なすべての値についての制約条件は満足しない：

パラメータの特定の値について求まった最大値はロバストな最大値以上である：

NMaxValueは線形計画問題を解くことができる：

LinearProgrammingを使って行列記法で与えられた同じ問題を解くことができる：

RegionBoundsを使って境界ボックスを計算する：

NMaxValueおよびNMinValueを使って同じ境界を計算する：

Wolfram Research (2008), NMaxValue, Wolfram言語関数， https://reference.wolfram.com/language/ref/NMaxValue.html （2024年に更新）.

テキスト

Wolfram Research (2008), NMaxValue, Wolfram言語関数， https://reference.wolfram.com/language/ref/NMaxValue.html （2024年に更新）.

CMS

Wolfram Language. 2008. "NMaxValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/NMaxValue.html.

APA

Wolfram Language. (2008). NMaxValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NMaxValue.html

BibTeX

@misc{reference.wolfram_2024_nmaxvalue, author="Wolfram Research", title="{NMaxValue}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/NMaxValue.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_nmaxvalue, organization={Wolfram Research}, title={NMaxValue}, year={2024}, url={https://reference.wolfram.com/language/ref/NMaxValue.html}, note=[Accessed: 21-November-2024 ]}