NMaxValue

NMaxValue[f,x]

给出关于 x 的 f 的全局最大值.

NMaxValue[f,{x,y,…}]

给出关于 x、y、 … 的 f 的全局最大值.

NMaxValue[{f,cons},{x,y,…}]

给出约束条件 cons 限制下 f 的全局最大值.

NMaxValue[…,x∈reg]

将 x 限制在区域 reg 内.

更多信息和选项

  • NMaxValue 亦称为全局优化 (GO).
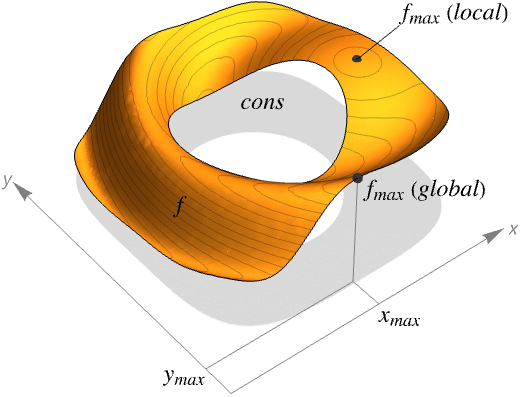
  • NMaxValue 总是尝试求给定约束条件限制下 f 的全局最大值.
  • NMaxValue 通常用于求给定约束条件下可能的最大值. 在不同的领域，这可能被称为最佳策略、最佳方案、最佳配置等.
  • 如果 f 是线性的或凹的，cons 是线性的或凸的，NMaxValue 给出的结果将是实数和整数值上的全局最大值；否则，有时结果可能只是局部最大值.
  • 如果 NMaxValue 发现无法满足约束条件，则会返回 -Infinity.
  • NMaxValue 支持一种建模语言，其中目标函数 f 和约束条件 cons 是用依赖于标量或向量变量的表达式给出的. f 和 cons 通常被解析为非常有效的形式，但只要 f 和 cons 中的项给出变量的数值结果，NMaxValue 通常可以找到解.
  • 约束条件 cons 可以是以下表达式的任意逻辑组合：
  • lhs==rhs等式
    lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhs不等式 (LessEqual、…)
    lhsrhs, lhsrhs, lhsrhs, lhsrhs向量不等式 (VectorLessEqual、…)
    {x,y,…}∈rdom区域或域的指定
  • NMaxValue[{f,cons},x∈rdom] 实际上等价于 NMaxValue[{f,cons&&x∈rdom},x].
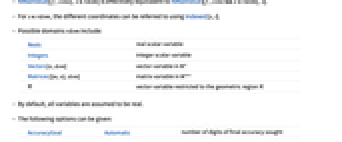
  • 对于 x∈rdom，可用 Indexed[x,i] 来指代不同的坐标.
  • 可能的域 rdom 包括：
  • Reals实标量变量
    Integers整数标量变量
    Vectors[n,dom] 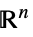中的向量变量
    Matrices[{m,n},dom] 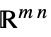中的矩阵变量
    ℛ限制在几何区域 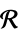中的向量变量
  • 在缺省情况下，假定所有变量为实数.
  • 可给出以下选项:
  • AccuracyGoalAutomatic追求多少位的准确度
    EvaluationMonitor None计算 f 时要计算的表达式
    MaxIterationsAutomatic使用的最大迭代次数
    Method Automatic使用的方法
    PrecisionGoalAutomatic追求多少位的精度
    StepMonitor None每次迭代时要计算的表达式
    WorkingPrecision MachinePrecision内部计算使用的精度
  • AccuracyGoal 和 PrecisionGoal 的设置指定了搜索最大值所在位置（最大化点）和函数的最大值时应使用的位数.
  • NMaxValue 持续运行，直到 AccuracyGoal 或 PrecisionGoal 指定的目标实现为止.
  • NMaxValue 的方法分为两类. 第一类方法利用问题的属性，因此当方法收敛时，找到的最大值保证是全局的. 第二类启发式方法使用的方法可能包括多个局部搜索，通常通过一些随机性进行调整以锁定全局最大值. 这些方法通常能找到全局最大值，但无法保证.
  • 在收敛到解时确保可以给出全局最大值的方法包括：
  • "Convex"只使用凸方法
    "MOSEK"对于凸问题，使用商用 MOSEK 库
    "Gurobi"对于凸问题，使用商用 Gurobi 库
    "Xpress"对于凸问题，使用商用 Xpress 库
  • 启发式方法包括：
  • "NelderMead"Nelder 和 Mead 的单纯形法
    "DifferentialEvolution"使用差分进化
    "SimulatedAnnealing"使用模拟退火
    "RandomSearch"使用从多个随机起始点中找到的最佳局部最大值
    "Couenne"使用 Couenne 库处理非凸混合整数非线性问题

范例

打开所有单元关闭所有单元

基本范例  (5)

求一元函数的最大值：

求多元函数的最大值：

求受约束条件限制的函数的最大值：

求函数在几何区域上的全局最大值：

求函数在几何区域上的全局最大值：

范围  (34)

基本用法  (12)

最大化受约束条件 限制的 ：

可用 VectorGreaterEqual 表示几个线性不等式约束条件：

用 v>= 或 \[VectorGreaterEqual] 输入向量不等式符号 ：

用标量不等式给出的等价形式：

使用向量变量 ：

由于 中可能存在的逐项运算，不等式 不一定和 一样：

如果想要避免 中不想要的逐项运算，可使用 Inactive[Plus]：

用常参数方程来避免 中不想要的逐项运算：

VectorGreaterEqual 表示关于 "NonNegativeCone" 的锥不等式：

如果想明确指定锥体的尺寸，可使用 {"NonNegativeCone",n}：

求解：

最大化受约束条件 限制的 ：

用含有 "NormCone" 的锥不等式指定约束条件 ：

求解：

最大化受约束条件 限制的函数 ：

用 Indexed 访问向量变量的分量，如 TemplateBox[{x, 1}, IndexedDefault]：

当向量变量不明确时，用 Vectors[n,dom] 指定维度和域：

用 NonNegativeReals (TemplateBox[{}, NonNegativeReals]) 指定非负约束条件：

用向量不等式 表示的等价格式：

用 NonPositiveReals (TemplateBox[{}, NonPositiveReals]) 指定非正约束条件：

用向量不等式表示的等价格式：

可以指定 Or 约束条件：

域约束条件  (4)

用 Integers 指定整数域约束条件：

用 Vectors[n,Integers] 指定向量变量的整数域约束条件：

用 NonNegativeIntegers (TemplateBox[{}, NonNegativeIntegers]) 指定非负整数域约束条件：

用 NonPositiveIntegers (TemplateBox[{}, NonPositiveIntegers]) 指定非正整数域约束条件：

区域约束条件  (3)

求向量线性函数的最大值， 是 中的一个向量，且 TemplateBox[{x}, Norm]<=1：

求区域上的最大值：

求被限制在两个不同区域的两点之间可能的最大距离：

线性问题  (5)

如果目标函数和约束条件是线性的，最大值即是全局最大值：

约束条件可以是等式和不等式约束条件：

用 Equal 一次表示几个等式约束条件：

用几个标量等式表示的等价形式：

用 VectorLessEqual 一次表示几个 LessEqual 不等式约束条件：

用 v<= 以紧凑格式输入向量不等式：

用标量不等式给出的等价形式：

用 Interval 指定变量的范围：

凸问题  (4)

用 "NonNegativeCone" 指定形如 的线性函数：

用 v>= 以紧凑格式输入向量不等式：

求受一组凸二次约束条件限制的凹二次函数的最大值：

绘制区域：

求 的使得 为半正定的最大值：

显示目标函数图：

求凹目标函数 的使得 为半正定且 的最大值：

绘制区域和最大化点：

可转化为凸问题的问题  (3)

最大化受不等式和范数约束条件限制的拟凹函数 . 目标函数是拟凹的，因为它是两个非负仿射函数的乘积：

最大化是通过最小化目标函数的负值 （拟凸函数）来解决的. 可将拟凸问题作为参数 的参数凸优化问题求解：

绘制作为水平子集 的函数的目标函数：

对于水平子集在区间 内的值，找到最小的值：

当水平集值增加时，问题变得不可行：

根据约束条件 最大化 . 目标是非凸但可通过凸差函数 表示，其中 和 为凸函数：

绘制该区域和最小化点：

根据约束条件 最大化 . 约束条件 为非凸但可通过凸差约束条件 表示，其中 和 为凸函数：

绘制该区域和最小化点：

普通问题  (3)

最大化受非线性约束条件限制的线性目标函数：

绘制这些值：

最大化受线性约束条件限制的非线性目标函数：

绘制目标函数和最大化点：

最大化受非线性约束条件限制的非线性目标函数：

绘制这些值：

选项  (7)

AccuracyGoal & PrecisionGoal  (2)

强调收敛标准 和 ：

强调收敛标准 和 ，这在使用默认机器精度的计算中是无法实现的：

设置一个较高的 WorkingPrecision，使过程收敛：

EvaluationMonitor  (1)

记录所有在求解有极小值环的函数过程中计算过的点：

绘制目标函数值接近最终答案的所有访问过的点：

Method  (2)

对于某些问题，某些方法可能会给出次优结果：

自动选择的方法给出了该问题的最优解：

为下面的非凸问题自动选择的方法为 "Couenne"：

绘制目标函数和全局最大值：

当速度至关重要时，请使用方法 "NelderMead" 来求解有多个变量的问题：

StepMonitor  (1)

NMaxValue 在求函数最大值的过程中采取的步骤：

WorkingPrecision  (1)

工作精度设为 时，AccuracyGoal 和 PrecisionGoal 默认值为 ：

应用  (4)

几何问题  (2)

求使得三角形和椭圆仍然相交的最大的 ：

绘制所得区域：

求圆的最大半径 ，使得 个非重叠圆和其中心都包含在一个 正方形内. 边界约束条件可表达为 ：

圆不可重叠：

组合这些变量：

求最大半径 ：

投资问题  (1)

求如何在两只股票和债券之间分配最多可达 $250,000 的资金，使得投资回报最大化. 令 为投资在两只股票上的金额， 为投资在债券上的金额：

投资于公用事业股票的金额不得超过 $40,000：

投资于债券的金额不能少于 $70,000：

投资于两只股票的总金额必须至少是投资总额的一半：

股票每年分别支付 9% 和 4% 的股息. 债券的股息为 5%. 总投资回报为：

执行交易的成本为 ，不能超过 $1000：

在指定约束条件下可获得的最大利润为：

迭代优化  (1)

求与椭圆 相关的参数 的值，使得 的最大值被最小化：

显示距离随 变化的情况：

求最小化目标函数的最大值的最佳参数 ：

属性和关系  (7)

NMaximize 给出最大值，并以规则形式给出使结果最大化的变量值：

NArgMax 给出使结果最大化的值的列表：

NMaxValue 只给出最大值：

最大化函数 f 相当于最小化 -f：

对于凸问题，可用 ConvexOptimization 获取解的其他属性：

获取对偶问题的解：

对于含有参数的凸问题，用 ParametricConvexOptimization 给出 ParametricFunction：

可通过计算 ParametricFunction 求得参数的值：

用 NMaxValue 定义参数化问题的函数：

比较两种方法的速度：

也可以计算 ParametricFunction 的导数：

对于含有参数化约束条件的凸问题，RobustConvexOptimization 将找到适用于所有可能参数值的最优值：

对于特定参数值，NMaxValue 可能会找到更大的最大值：

对于 和 允许的所有值，该最大化点不满足约束条件：

为特定参数值找到的最大值大于或等于稳健最大值：

NMaxValue 可以求解线性规划问题：

LinearProgramming 可以求解用矩阵表示的相同问题：

用 RegionBounds 计算边界框：

用 NMaxValue 和 NMinValue 计算相同的边界：

Wolfram Research (2008)，NMaxValue，Wolfram 语言函数，https://reference.wolfram.com/language/ref/NMaxValue.html （更新于 2024 年）.

文本

Wolfram Research (2008)，NMaxValue，Wolfram 语言函数，https://reference.wolfram.com/language/ref/NMaxValue.html （更新于 2024 年）.

CMS

Wolfram 语言. 2008. "NMaxValue." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/NMaxValue.html.

APA

Wolfram 语言. (2008). NMaxValue. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NMaxValue.html 年

BibTeX

@misc{reference.wolfram_2024_nmaxvalue, author="Wolfram Research", title="{NMaxValue}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/NMaxValue.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_nmaxvalue, organization={Wolfram Research}, title={NMaxValue}, year={2024}, url={https://reference.wolfram.com/language/ref/NMaxValue.html}, note=[Accessed: 21-November-2024 ]}