NSurfaceIntegrate

NSurfaceIntegrate[f,{x,y,…}∈surface]

関数 f[x,y,…]の数値スカラー面積分を surface 上で計算する．

NSurfaceIntegrate[{p,q,…},{x,y,…}∈surface]

ベクトル場{p[x,y,…],q[x,y,…],…}の数値ベクトル面積分を計算する．

詳細とオプション

  • 面積分は流束積分としても知られている．
  • スカラー面積分は，超曲面上でスカラー関数を積分するもので，曲面の面積，質量，電荷等の計算によく使われる．
  • ベクトル面積分は，法線方向に曲面を通るベクトル関数の流束の計算に使われる．典型的なベクトル関数には，流体速度場，電場，磁場が含まれる．
  • 関数 f の surface 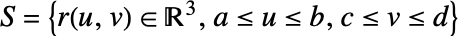上のスカラー面積分は以下で与えられる．
  • ただし，TemplateBox[{{{{partial, _, u}, {r, (, {u, ,, v}, )}}, x, {{partial, _, v}, {r, (, {u, ,, v}, )}}}}, Norm]はパラメトリック曲面の要素の尺度である．
  • 超曲面 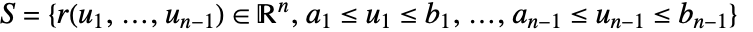上の f のスカラー面積分は以下で与えられる．

  • スカラー面積分は，surface のパラメトリック化と向きには依存しない．surface には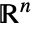，における任意の 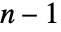次元のRegionQオブジェクトを使うことができる．
  • ベクトル関数 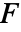の surface 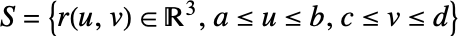上のベクトル面積分は以下で与えられる．
  • ただし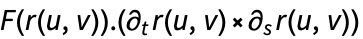，F(r(u,v)).(partial_tr(u,v)xpartial_sr(u,v))はベクトル関数 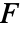の法線方向への投影なので，積分されるのは法線方向の成分だけである．
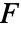  • の超曲面 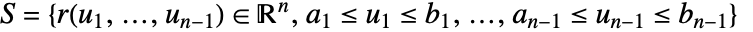上のベクトル面積分は以下で与えられる．

  • ベクトル面積分はパラメータ化からは独立であるが，方向には依存する．
  • 超曲面の方向は，曲面上の法線ベクトル場 によって与えられる．
  • パラメトリック超曲面ParametricRegion[{r1[u1,…,un-1],…,rn[u1,…,un-1]},…]について，法線ベクトル場 はCross[∂u1r[u],…,∂un-1r[u]]であるとみなされる．
  • Wolfram言語におけるRegionQオブジェクトは方向を持たない．しかし，この関数の便宜上，方向を持つ超曲面を得るために以下の規則を想定することができる．
  • （次元 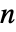の）立体と境界を持つRegionQオブジェクト ℛ について，曲面は領域境界(RegionBoundary[ℛ]) であり法線方向は外側に向いていると仮定する．
  • 次は，の特殊な立体と想定される境界面（辺）の法線方向である．
  • Triangle外向き法線
    Rectangle外向き法線
    Polygon外向き法線
    Disk外向き法線
    Ellipsoid外向き法線
    Annulus外向き法線
  • 次は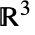， の特殊な立体と想定される境界面（面）の法線方向である．
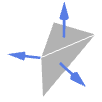
  • Tetrahedron外向き法線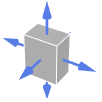
    Cuboid外向き法線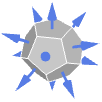
    Polyhedron外向き法線
    Ball外向き法線
    Ellipsoid外向き法線
    Cylinder外向き法線
    Cone外向き法線
  • 次は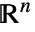， の特殊な立体と想定される境界面（ファセット）の法線方向である．
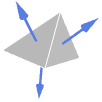
  • Simplex外向き法線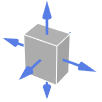
    Cuboid外向き法線
    Ball外向き法線
    Ellipsoid外向き法線
  • 次は，使用可能なオプションである．
  • AccuracyGoal Automatic目標絶対確度の桁数
    MaxPoints Automaticサンプル点の最大総数
    MaxRecursion Automatic再帰的下位区分の最大数
    Method Automatic使用するメソッド
    MinRecursion 0再帰的下位区分の最小数
    PrecisionGoal Automatic目標精度の桁数
    WorkingPrecision Automatic内部計算精度

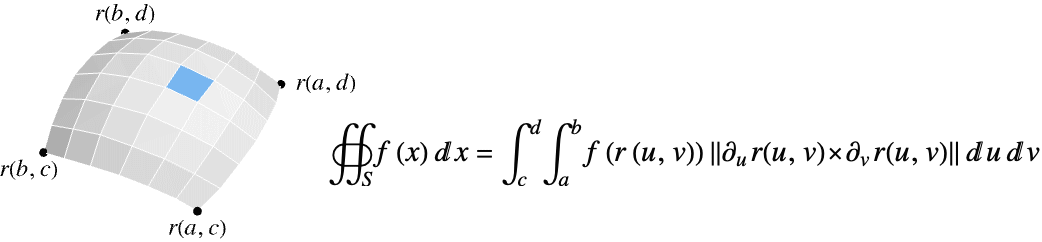
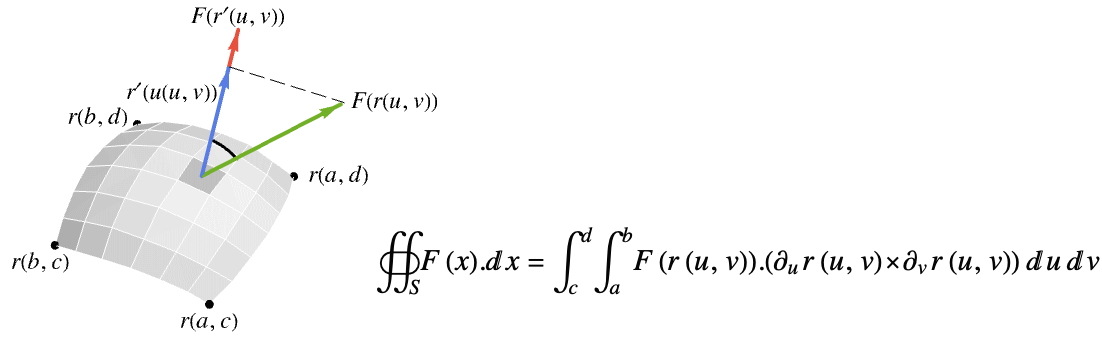
例題

すべて開くすべて閉じる

例  (6)

球面上のスカラー関数の面積分：

球面上のベクトル場の面積分：

パラメトリック曲面上のスカラー場の面積分：

パラメトリック曲面上のベクトル場の面積分：

曲面上のスカラー場の面積分：

スカラー場を曲面上で可視化する：

曲面上のベクトル場の面積分：

曲面上でスカラー場を可視化する：

スコープ  (32)

基本的な用法  (5)

三次元の立方体上におけるスカラー場の面積分：

三次元のベクトル場の面積分：

SurfaceIntegrateは多くの特殊曲面に使うことができる：

パラメトリック曲面上の面積分：

SurfaceIntegrateは三次元以外の次元で使うことができる：

スカラー関数  (5)

三次元曲面上のスカラー場の面積分：

曲面のプロット：

面積分：

三角形上のスカラー場の面積分：

面積分：

球上の三次元におけるスカラー場の面積分：

角錐の面の上のスカラー場の面積分：

面積分：

三次元パラメトリック曲面上のスカラー場の面積分：

面とそのプロット：

ベクトル関数  (5)

球面上の三次元ベクトル場の面積分：

曲面上にベクトル場を可視化する：

面積分：

三角形上の三次元のベクトル場の面積分：

面積分：

三次元パラメトリック曲面上のベクトル場の面積分：

楕円体の境界上のベクトル場の面積分：

円錐の境界上の三次元のベクトル場の面積分：

曲面上のベクトル場の可視化：

面積分：

特殊曲面  (10)

半径1の球面上のベクトル場の面積分：

原点を中心とする立方体の境界上でのベクトル場の面積分：

四面体の境界上でのベクトル場の面積分：

三角形上でのベクトル場の面積分：

楕円体上でのベクトル場の面積分：

円錐の境界上でのベクトル場の面積分：

円筒の境界上でのベクトル場の面積分：

平行六面体の境界上でのベクトル場の面積分：

角柱の境界上でのベクトル場の面積分：

三次元における多角形上での面積分：

多角形の向きは点が与えられた順序に依存する：

パラメトリック曲面  (4)

パラメトリック曲面上でのベクトル場での面積分：

パラメータ化されたドームのような曲面上でのベクトル場の面積分：

パラメータ化された円筒上での面積分：

パラメータ化された双曲面上でのベクトル場の面積分：

超曲面  (3)

2Dにおける1D超曲面上での面積分：

4Dにおける3D超曲面上での面積分：

面積分を使って計算された五次元球の体積：

オプション  (8)

AccuracyGoal  (1)

オプションAccuracyGoalは確度の桁数を設定する：

デフォルト設定での結果はPrecisionGoalしか設定しない：

MaxPoints  (1)

オプションMaxPointsは指定数の点の評価が終ると積分を中止する：

デフォルトオプションでは以下のようになる：

MaxRecursion  (1)

オプションMaxRecursionは再帰ステップの最大数を指定する：

再帰回数を増やす：

Method  (1)

オプションMethodはNIntegrateと同じ値を取る．例として以下を見よ：

デフォルトオプションでは以下のようになる：

MinRecursion  (1)

ピークが急峻な関数に便利なオプションのMinRecursionは，下位区分の最小数を矯正する：

厳密な結果と比較する：

PrecisionGoal  (1)

オプションPrecisionGoalは積分における相対的な許容範囲を設定する：

デフォルト設定を使うと以下のようになる：

WorkingPrecision  (2)

WorkingPrecisionが指定されていると，計算はその作業制度を使って行われる：

被積分関数は有限精度かもしれない：

アプリケーション  (18)

大学の微積分  (5)

原点を中心とした1辺が2の立方体の境界上の面積分：

放物体上の面積分：

円筒の側面上の面積分：

半径2の半球シェル上の面積分：

立方体の境界上の面積分：

面積  (3)

球の面積：

楕円体の面積：

三角形の面積：

体積  (3)

面積分を使って計算した楕円体の体積：

面積分を使って計算した20面体の体積：

面積分を使って計算した1辺が3の立方体の体積：

磁束  (3)

原点の点電荷 によって原点を取り囲む球上に生成された電場の磁束：

単位長あたり 個の巻線を持ち，それに直交する円板上を電流 　が通過する無限ソレノイドの均一磁場の磁束：

線形電荷密度 の無限帯電ワイヤによる電場：

帯電ワイヤ上に軸を持つ高さ ，半径 の円柱を横切る磁束：

重心  (2)

単位密度で半径が の半球シェルの質量：

質量の中心の 座標：

質量の中心の 座標：

質量の中心の 座標：

薄く切り取られた円錐の慣性モーメント：

軸の周りの：

軸の周りの：

軸の周りの：

古典的な定理  (2)

ストークス(Stokes)の定理．ベクトル場 のCurl の面積分：

開いた曲面上の の面積分：

これは，曲面の境界上の の線積分に等しい：

発散定理．閉じた曲面上のベクトル場 （連続偏導関数を含む）の面積分は以下の通りである：

これは，曲面の内側におけるDiv[f]の積分と同じである：

特性と関係  (5)

記号計算ができない場合はN[SurfaceIntegrate[…]]を適用してNSurfaceIntegrateで数値解を得る：

単位面積あたり単位質量である薄い三角形の表面の重心を求める：

総質量を求める：

重心の 成分を求める：

重心の 成分を求める：

重心の 成分を求める：

重心はRegionCentroidを使って求めることもできる：

単位面積密度の薄い円筒シェルの 軸の周りの慣性モーメントを求める：

答はMomentOfInertiaで計算することもできる：

四面体の面積を求める：

答はSurfaceAreaで計算することもできる：

20面体の体積を求める：

答はVolumeで計算することもできる：

おもしろい例題  (9)

面積分を使って計算した擬球の体積：

擬球の有限部分のプロット：

面積分を使って計算された雫型の立体の体積：

Dupinサイクライドの体積：

ボヘミアンドームの一部を横切るベクトル場上の磁束：

Wallisの円錐形の一部の上でのベクトル場の面積分：

漏斗状の曲面の上でのベクトル場の面積分：

ガウディ曲面の面積：

Guimard曲面の面積を数値的に計算する：

Neiloid上のベクトル場の面積分：

Wolfram Research (2024), NSurfaceIntegrate, Wolfram言語関数， https://reference.wolfram.com/language/ref/NSurfaceIntegrate.html.

テキスト

Wolfram Research (2024), NSurfaceIntegrate, Wolfram言語関数， https://reference.wolfram.com/language/ref/NSurfaceIntegrate.html.

CMS

Wolfram Language. 2024. "NSurfaceIntegrate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NSurfaceIntegrate.html.

APA

Wolfram Language. (2024). NSurfaceIntegrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NSurfaceIntegrate.html

BibTeX

@misc{reference.wolfram_2024_nsurfaceintegrate, author="Wolfram Research", title="{NSurfaceIntegrate}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/NSurfaceIntegrate.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_nsurfaceintegrate, organization={Wolfram Research}, title={NSurfaceIntegrate}, year={2024}, url={https://reference.wolfram.com/language/ref/NSurfaceIntegrate.html}, note=[Accessed: 05-November-2024 ]}