Periodogram

Periodogram[list]

plots the squared magnitude of the discrete Fourier transform (power spectrum) of list.

Periodogram[list,n]

plots the mean of power spectra of non-overlapping partitions of length n.

Periodogram[list,n,d]

uses partitions with offset d.

Periodogram[list,n,d,wfun]

applies a smoothing window wfun to each partition.

Periodogram[list,n,d,wfun,m]

pads partitions with zeros to length m prior to the computation of the transform.

Periodogram[{list1,list2,…},n,d,wfun,m]

plots power spectra of several lists.

Periodogram[audio,…]

plots the power spectrum of audio.

Periodogram[video,…]

plots the power spectrum of the first audio track in video.

Periodogram[{input1,input2,…},…]

plots the power spectra of all inputi.

Details and Options

  • Periodogram shows the frequency content of a signal by plotting the magnitude squared of the discrete Fourier transform.
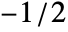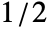  • In Periodogram[list,n,d,wfun], the smoothing window wfun can be specified using a window function that will be sampled between and , or a list of length n. The default window is DirichletWindow, which effectively does no smoothing.
  • Periodogram[list,n] is equivalent to Periodogram[list,n,n,DirichletWindow,n].
  • Periodogram works with numeric lists as well as Audio and Sound objects.
  • For a multichannel sound object, Periodogram plots power spectra of all channels.
  • For real input data, Periodogram displays only the first half of the power spectrum due to the symmetry property of the Fourier transform.
  • Compute the effective power spectrum using PeriodogramArray.
  • Periodogram takes the following options:
  • FourierParameters {0,1}Fourier parameters
    SampleRate Automaticthe sample rate
    ScalingFunctions {"Linear","dB"}the scaling function
  • With the setting SampleRate->r, signal frequencies are shown in the range from 0 to r/2.
  • Possible settings for ScalingFunctions include:
  • Automaticautomatic scaling
    Nonelinear scaling for 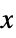axis and absolute scaling for 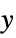axis
    sy 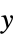axis scaling
    {sx} 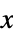axis scaling
    {sx,sy}different scaling functions for the 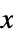and directions
  • Possible magnitude scalings sy include:
  • "Absolute"absolute scaling
    "dB" 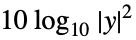decibel scaling (default)
    {f,f-1}arbitrary scaling using the function f and its inverse
  • Possible frequency scalings sx include:
  • "Linear"linear scaling (default)
    "Log10" 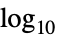scaling
    {f,f-1}arbitrary scaling using the function f and its inverse
  • The scaling function can be "dB" or "Absolute", which correspond to the decibel and absolute power values, respectively.
  • Periodogram also accepts all options of ListLinePlot.

Examples

open allclose all

Basic Examples  (3)

Power spectrum of a noisy dataset:

Periodogram of a Sound object:

Power spectrum of an Audio object:

Scope  (4)

Bartlett's method averages over non-overlapping partitions:

Average overlapping partitions:

Welch's method averages over smoothed overlapping partitions:

Pad each partition to increase plot density:

Power spectrum of two dual-tone multi-frequency (DTMF) signals:

Periodogram of a multichannel audio object:

Periodogram of the audio track of a video:

Options  (4)

DataRange  (1)

Use DataRange to display the power spectrum on the normalized frequency range {0,Pi} radians per unit time:

FourierParameters  (1)

Changing the a parameter in FourierParameters will change the scaling:

SampleRate  (1)

By default, Periodogram assumes a sampling rate of one sample per time unit:

Specify a different sample rate:

ScalingFunctions  (1)

By default, Periodogram shows the decibel values of magnitude:

Show the absolute values of the periodogram magnitude:

Properties & Relations  (1)

Periodogram plots the magnitude squared of the Fourier transform:

Possible Issues  (2)

When an explicit DataRange is specified, the SampleRate setting is ignored:

For very large partitions with a smoothing window, timing is increased due to sampling of the window:

Specify a smaller partition size:

Timing will be even worse with no partitioning:

Wolfram Research (2012), Periodogram, Wolfram Language function, https://reference.wolfram.com/language/ref/Periodogram.html (updated 2024).

Text

Wolfram Research (2012), Periodogram, Wolfram Language function, https://reference.wolfram.com/language/ref/Periodogram.html (updated 2024).

CMS

Wolfram Language. 2012. "Periodogram." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Periodogram.html.

APA

Wolfram Language. (2012). Periodogram. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Periodogram.html

BibTeX

@misc{reference.wolfram_2024_periodogram, author="Wolfram Research", title="{Periodogram}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Periodogram.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_periodogram, organization={Wolfram Research}, title={Periodogram}, year={2024}, url={https://reference.wolfram.com/language/ref/Periodogram.html}, note=[Accessed: 14-November-2024 ]}