Periodogram

Periodogram[list]

list の離散フーリエ(Fourier)変換の振幅の二乗（パワースペクトル）をプロットする．

Periodogram[list,n]

長さ n の重なり合わないパーティションのパワースペクトルの平均をプロットする．

Periodogram[list,n,d]

オフセット d でパーティションを使う．

Periodogram[list,n,d,wfun]

各パーティションに平滑化窓 wfun を適用する．

Periodogram[list,n,d,wfun,m]

変換を計算する前に，長さ m になるまでパーティションを0で充填する．

Periodogram[{list1,list2,…},n,d,wfun,m]

複数のリストのパワースペクトルをプロットする．

Periodogram[audio,…]

audio のパワースペクトルをプロットする．

Periodogram[video,…]

video の最初の音声トラックのパワースペクトルをプロットする．

Periodogram[{audio1,audio2,…},…]

全 audioiのパワースペクトルをプロットする．

詳細とオプション

  • Periodogramは，離散フーリエ変換の大きさの2乗をプロットすることで信号の周波数成分を示す．
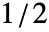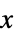  • Periodogram[list,n,d,wfun]では，からの範囲でサンプルされる窓関数あるいは長さ n のリストを使って平滑化窓 wfun を指定することができる．デフォルトの窓は事実上平滑化は行わないDirichletWindowである．
  • Periodogram[list,n]はPeriodogram[list,n,n,DirichletWindow,n]と等価である．
  • PeriodogramArrayを使って実質的なパワースペクトルを計算する．
  • 実数入力データについては，Periodogramはフーリエ変換の対称性により，パワースペクトルの前半分のみを表示する．
  • Periodogramは，数値リストとAudioおよびSoundの両オブジェクトに使うことができる．
  • 多チャンネルのサウンドオブジェクトについては，Periodogramは全チャンネルのパワースペクトルをプロットする．
  • Periodogramの取り得るオプション
  • FourierParameters {0,1}フーリエパラメータ
    SampleRate Automaticサンプルレート
    ScalingFunctions {"Linear","dB"}スケーリング関数
  • SampleRate->r の設定のとき，信号の周波数は0から r/2の範囲で示される．
  • ScalingFunctionsの可能な設定
  • Automatic自動スケーリング
    None 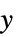軸に線形スケーリング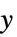， 軸に絶対スケーリング
    sy 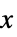軸スケーリング
    {sx} 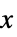軸スケーリング
    {sx,sy} 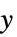方向と 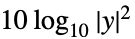方向に別々のスケーリング関数
  • 使用可能なマグニチュードスケーリング sy
  • "Absolute"絶対スケーリング
    "dB"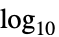デシベルスケーリング
    {f,f-1}関数 f とその逆関数を使った任意のスケーリング
  • 使用可能な周波数スケーリング sx
  • "Linear"線形スケーリング（デフォルト）
    "Log10"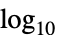スケーリング
    {f,f-1}関数 f とその逆関数を使った任意のスケーリング
  • スケーリング関数は，それぞれデシベルと絶対ベキ値に相当する"dB"あるいは"Absolute"でよい．
  • PeriodogramにはListLinePlotのすべてのオプションも使うことができる．

例題

すべて開くすべて閉じる

例  (3)

ノイズの多いデータ集合のパワースペクトル：

SoundオブジェクトのPeriodogram：

Audioオブジェクトのパワースペクトル：

スコープ  (4)

Bartlett法は重なり合ないパーティション上で平均する：

重なり合うパーティションの平均：

Welch法は平滑化された重なり合うパーティション上で平均する：

各パーティションを充填してプロット密度を上げる：

2つのデュアルトーン多周波(DTMF)信号のパワースペクトル：

多チャンネルオーディオオブジェクトのペリオドグラム：

動画の音声トラックのペリオドグラム：

オプション  (4)

DataRange  (1)

DataRangeを使って，正規化された周波数範囲{0,Pi}ラジアン／単位時間でパワースペクトルを表示する：

FourierParameters  (1)

FourierParameters中のパラメータaを変更するとスケーリングが変わる：

SampleRate  (1)

デフォルトで，Periodogramは1つのサンプルの単位時間あたりのサンプル抽出率を仮定する：

異なるサンプルレートを指定する：

ScalingFunctions  (1)

デフォルトで，Periodogramは振幅のデシベル値を示す：

ピリオドグラムの振幅の絶対値を示す：

特性と関係  (1)

Periodogramはフーリエ変換の振幅の二乗をプロットする：

考えられる問題  (2)

明示的なDataRangeを指定すると，SampleRateの設定は無視される：

平滑化窓がある非常に大きいパーティションについては，タイミングは窓のサンプリングに従って大きくされる：

小さいパーティションサイズを指定する：

パーティションがないと，タイミングはより悪くなる：

Wolfram Research (2012), Periodogram, Wolfram言語関数， https://reference.wolfram.com/language/ref/Periodogram.html （2024年に更新）.

テキスト

Wolfram Research (2012), Periodogram, Wolfram言語関数， https://reference.wolfram.com/language/ref/Periodogram.html （2024年に更新）.

CMS

Wolfram Language. 2012. "Periodogram." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Periodogram.html.

APA

Wolfram Language. (2012). Periodogram. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Periodogram.html

BibTeX

@misc{reference.wolfram_2024_periodogram, author="Wolfram Research", title="{Periodogram}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Periodogram.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_periodogram, organization={Wolfram Research}, title={Periodogram}, year={2024}, url={https://reference.wolfram.com/language/ref/Periodogram.html}, note=[Accessed: 14-November-2024 ]}