Periodogram

Periodogram[list]

绘制 list 的离散傅立叶变换（功率谱）的幅度平方.

Periodogram[list,n]

绘制长度为 n 的无重叠分区的功率谱的均值.

Periodogram[list,n,d]

使用具有偏移为 d 的分区.

Periodogram[list,n,d,wfun]

对每个分区使用平滑窗 wfun.

Periodogram[list,n,d,wfun,m]

在变换计算前，用0填充分区至长度为 m.

Periodogram[{list1,list2,…},n,d,wfun,m]

绘制多个列表的周期图.

Periodogram[audio,…]

绘制 audio 的功率谱.

Periodogram[video,…]

绘制 video 中第一条音轨的功率谱.

Periodogram[{input1,input2,…},…]

绘制所有 inputi 的功率谱.

更多信息和选项

  • Periodogram 通过绘制离散傅里叶变换幅度的平方来显示信号的频率内容.
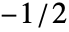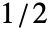  • 在 Periodogram[list,n,d,wfun] 中，平滑窗 wfun 可用在 和 之间采样或长度为 n 的列表的窗函数指定. 默认窗是 DirichletWindow，它没有进行有效的平滑处理.
  • Periodogram[list,n] 等价于 Periodogram[list,n,n,DirichletWindow,n].
  • Periodogram 可用于数字列表以及 Audio 和 Sound 对象.
  • 对于多通道声音对象，Periodogram 绘制所有通道的功率谱.
  • 对于实际的输入数据，因为傅立叶变换的对称性，Periodogram 只显示功率谱的前一半.
  • 用 PeriodogramArray 计算有效功率谱.
  • Periodogram 使用下列选项：
  • FourierParameters {0,1}傅里叶参数
    SampleRate Automatic采样率
    ScalingFunctions {"Linear","dB"}缩放函数
  • 设置 SampleRate->r 时，信号频率显示在范围 0 到 r/2 之间.
  • ScalingFunctions 的可能设置包括：
  • Automatic自动缩放
    None对 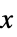轴进行线性缩放，对 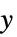轴进行绝对缩放
    sy 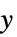轴缩放
    {sx} 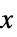轴缩放
    {sx,sy}在 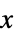和 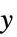方向采用不同的缩放函数
  • 幅值缩放 sy 的可能设置包括：
  • "Absolute"绝对缩放
    "dB" 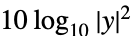分贝缩放（缺省）
    {f,f-1}使用函数 f 及其倒数进行任意缩放
  • 频率缩放 sx 的可能设置包括：
  • "Linear"线性缩放（缺省）
    "Log10" 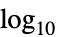缩放
    {f,f-1}使用函数 f 及其倒数进行任意缩放
  • 缩放函数可以是 "dB" 或者 "Absolute"，分别对应于分贝和绝对功率值.
  • Periodogram 也接受 ListLinePlot 的所有选项.

范例

打开所有单元关闭所有单元

基本范例  (3)

噪声数据集的功率谱：

Sound 对象的 Periodogram：

Audio 对象的功率谱：

范围  (4)

巴特利特（Bartlett）方法平均不重叠的分区：

平均重叠分区：

韦尔奇（Welch）方法平均平滑的重叠的分区：

填充每个划分以增加图线密度：

两个双音多频 (DTMF) 信号的功率谱：

多通道音频对象的周期图：

视频中的音轨的功率谱：

选项  (4)

DataRange  (1)

使用 DataRange 显示规范频率范围 {0,Pi} 内每单位时间的弧度的功率谱：

FourierParameters  (1)

改变 FourierParameters 中的 a 参数将改变缩放尺度：

SampleRate  (1)

默认情况下，Periodogram 假定每个时间单位一个样本的采样率：

指定一个不同的采样率：

ScalingFunctions  (1)

默认情况下，Periodogram 显示幅值组成的分贝值：

显示周期图幅度的绝对值：

属性和关系  (1)

Periodogram 绘制了傅里叶变换的幅度平方：

可能存在的问题  (2)

当指定显式的 DataRange 时，忽略 SampleRate 设置：

对于具有平滑窗口的相当大的划分，由于窗口采样，时间将增加：

指定更小的划分尺寸：

在没有划分的情况下，分时将更糟糕：

Wolfram Research (2012)，Periodogram，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Periodogram.html （更新于 2024 年）.

文本

Wolfram Research (2012)，Periodogram，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Periodogram.html （更新于 2024 年）.

CMS

Wolfram 语言. 2012. "Periodogram." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/Periodogram.html.

APA

Wolfram 语言. (2012). Periodogram. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Periodogram.html 年

BibTeX

@misc{reference.wolfram_2024_periodogram, author="Wolfram Research", title="{Periodogram}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Periodogram.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_periodogram, organization={Wolfram Research}, title={Periodogram}, year={2024}, url={https://reference.wolfram.com/language/ref/Periodogram.html}, note=[Accessed: 14-November-2024 ]}