Reduce

Reduce[expr,vars]

vars について方程式あるいは不等式を解き，限定子を除去することで，命題 expr を簡約する．

Reduce[expr,vars,dom]

領域 dom で簡約を行う．通常 dom はReals，Integers，Complexes等である．

詳細とオプション

  • 命題 expr は次の論理結合のいずれでもよい．
  • lhs==rhs等しい
    lhs!=rhs等しくない
    lhs>rhs または lhs>=rhs 不等式
    expr∈dom定義域指定
    {x,y,…}∈reg値域指定
    ForAll[x,cond,expr]全称記号
    Exists[x,cond,expr]存在記号
  • Reduce[expr,vars]の結果は常に expr と全く等しい数学的な集合を表す．
  • Reduce[{expr1,expr2,…},vars]はReduce[expr1&&expr2&&…,vars]と等価である．
  • Reduce[expr,vars]は，デフォルトで，不等式に代数的に現れる限定子は実数で，その他の限定子は複素数であると仮定する．
  • Reduce[expr,vars,dom]は，すべての変数とパラメータを定義域 dom に属するものに限る．
  • dom がRealsであるか，あるいはIntegersやRationalsのような部分集合の場合，すべての定数と関数の値もまた実数に限られる．
  • Reduce[expr&&vars∈Reals,vars,Complexes]は実数と仮定される変数の簡約を行うが，関数の値は複素数であっても構わない．
  • Reduce[expr,vars,Integers]は整数についてディオファントス(Diophantus)方程式を簡約する．
  • Reduce[…,x∈reg,Reals]は，x が値域 reg になるように制限する．x の異なる座標にはIndexed[x,i]を使って言及することができる．
  • Reduce[expr,{x1,x2,…},…]は，実質的に expr を x1, x2, …に対する制約条件の論理結合として表現する．ただし各条件は直前の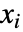のみが関連するものとする．
  • expr 中の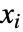を含まない代数的変数は独立パラメータとして扱われる．
  • Reduce[expr,…]の結果にLogicalExpandを適用すると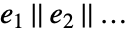，という形式の式が与えられる．ただし，各 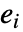は expr が定義する集合中の個々の構成要素であると考えられる．
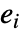  • は解体してはならないが，異なる次元を持つことはできる．LogicalExpandの後，各 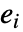は 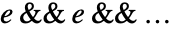という形式になる．
  • LogicalExpandがなければ，Reduceはデフォルトで 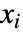の条件をネストしたものを連続したレベルでOrとAndを交互に組み合せて返す．
  • expr が実数あるいは複素数の定義域の整方程式と不等式のみを含む場合は，Reduceは原則的に常にすべての 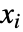について直接解くことができる．
  • expr が超越条件や整数の定義域を含んでいる場合，Reduceはしばしば結果に付加的なパラメータを導入する．
  • expr が多項式条件のみを含む場合，Reduce[expr,vars,Reals]は expr の柱状代数分解(CAD)を与える．
  • Reduceは整数についてのすべての線形方程式と不等式の明示的な解の表示を与えることができ，文献中のディオファントス方程式の大部分を解くことができる．
  • expr が実数または複素数の定義域で多項式条件のみを含む場合，Reduce[expr,vars]は結果に数量的変数が含まれないように常に限定子を除去する．
  • 指定可能なオプション
  • Backsubstitution False逆置換によってほどいた結果を与えるか否か »
    Cubics Falseすべての三次関数を解くために明示的な根号を使うか否か »
    GeneratedParameters C生成したパラメータの命名法 »
    Modulus 0整数に仮定するモジュール »
    Quartics False四次方程式を解くために明示的な根号を使うか否か »
  • Reduce[expr,{x1,x2,…},Backsubstitution->True]は，特定の 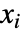の条件が以前の 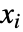に最低限しか依存しないように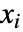，のために以前に生成された方程式の値が逆置換された形を与える． »

例題

すべて開くすべて閉じる

例  (4)

方程式と不等式を簡約する：

特定の定義域を使う：

数量化された式を簡約する：

幾何学領域の条件で簡約する：

スコープ  (83)

基本的な用法  (5)

方程式系の解集合の明示的な記述を求める：

ToRulesおよびReplaceRepeated (//.)を使って解をリストにする：

不等式系の解集合の明示的な記述を求める：

指定された定義域上で解を求める：

解集合が記号パラメータに依存することがある：

解を表すためには新たなパラメータを導入する必要があるかもしれない：

最初の10個の解をリストにする：

複素領域  (16)

線形系：

一変数整方程式：

多変数整方程式：

整方程式系と整非等式系は常に簡約できる：

数量化された多項式系：

代数系：

逆関数を使って可解の超越方程式：

この場合は解がない：

楕円関数を含む方程式：

特殊関数の零点を使って可解な方程式：

この系を解くのにリーマン(Riemann)仮説は必要ない：

境界有界範囲における初等関数方程式：

有界範囲における正則関数方程式：

以下ではReduceがある種の解を求めたが，他の解がないことは証明できない：

複素平面の縦縞上で純粋に虚数の循環小数を含む方程式：

二重周期の超越方程式：

逆関数を使って可解の超越方程式系：

有界ボックス上の解析方程式の二乗系：

実領域  (26)

線形系：

一変数整方程式：

一変数整不等式：

多変数整方程式：

多変数整不等式：

整方程式系と整不等式系は常に簡約できる：

数量化された多項式系：

代数系：

区分方程式：

区分不等式：

逆関数を用いて可解な超越方程式：

逆関数を用いて可解な超越不等式：

楕円方程式を含む不等式：

特殊関数の零点を用いて可解な超越方程式：

特殊関数の零点を用いて可解な超越不等式：

指数対数方程式：

高次の疎な整方程式：

高次の根基を含む代数方程式：

非有理実数ベキを含む方程式：

指数対数不等式：

有界範囲における初等関数方程式：

有界範囲における正則関数方程式：

有界範囲における有理型関数不等式：

実数上の周期初等関数方程式：

逆関数を用いて可解な超越系：

第1変数に指数対数，その他の変数に多項式を持った系：

量化された系：

第1変数が初等および有界，他の変数に多項式を持った系：

量化された系：

第1変数が解析的で有界，他の変数に多項式がある系：

量化された系：

有界領域上の解析方程式の二乗系：

整数領域  (13)

方程式の線形系：

方程式と不等式の線形系：

一変数整方程式：

一変数整不等式：

バイナリ二次方程式：

トゥエ(Thue)方程式：

平方和方程式：

ピタゴラス方程式：

方程式と不等式の境界を持った系：

解を持たない高次の系：

超越ディオファントス系：

合同の多項式系：

無理係数を持つディオファントス方程式：

モジュラ領域  (5)

線形系：

一変数整方程式：

多変数整方程式：

整方程式系と整非不等式系：

数量化された多項式系を簡約する：

有限体領域  (4)

　一変量方程式：

線形方程式系：

整方程式系：

限定子を含む系：

混合領域  (4)

実変数と複素変数の混合：

が実数でより小さい場合について， の実数値と の複素数値を求める：

Abs[x]を含む不等式を簡約する：

解集合をプロットする：

整数と実数の変数を混ぜる：

幾何学領域  (10)

変数を2Dの基本的な幾何学領域に制限する：

解をプロットする：

変数を3Dにおける基本的な幾何学領域に制限する：

解をプロットする：

3D領域を - 平面に投影する：

投影をプロットする：

陰的に定義された領域：

パラメトリックに定義された領域：

派生領域：

の解は交差を制限する：

領域の直積上で限定子を除去する：

パラメータに依存する領域：

についての条件：

を使って が内のベクトルであると指定する：

この場合は， は’内のベクトルである：

オプション  (6)

Backsubstitution  (1)

変数のリスト中でyはxの後ろに現れるので，Reduceはyについての解を表すのにxを使うかもしれない：

Backsubstitution->Trueのとき，Reduceはyの明示的な数値を返す：

Cubics  (1)

デフォルトでは，Reduceは三次方程式を根基で解く一般的な公式は使わない：

Cubics->Trueとすると，Reduceはすべての三次方程式を根基を用いて解く：

GeneratedParameters  (1)

Reduceは，解を表すために新たなパラメータを導入することがある：

GeneratedParametersを使ってパラメータの生成方法を制御する：

Modulus  (1)

9を法として整数上で方程式を解く：

Quartics  (1)

デフォルトでは，Reduceは四次方程式を根基で解く一般的な公式は使わない：

Quartics->Trueとすると，Reduceはすべての四次方程式を根基によって解く：

WorkingPrecision  (1)

厳密計算で解を求めようとすると時間がかかる：

WorkingPrecision->100を使うと，Reduceは速く解を求められるようになるが，求まった解は正しくないかもしれない：

アプリケーション  (9)

基本的なアプリケーション  (1)

三角形の辺 ，， について幾何不等式を証明する：

三角形についての不等式を証明する：

鋭角三角形についての不等式を証明する：

多項式の根に関する問題  (1)

四次方程式のすべての根が同じになる条件を求める：

限定子の消去を使う：

Subresultantsを使う：

パラメータ化問題  (1)

陰的な説明によって与えられた空間曲線をプロットする：

空間曲線の - 平面への投影をプロットする：

整数問題  (3)

ピタゴラス(Pythagoras)の3数を求める：

連続するピタゴラスの3数を求める：

2ドル27セントの郵送料を払うための，10セント，23セント，27セントの切手の組合せ方を求める：

IntegerPartitionsを使っても同じタスクを行うことができる：

正多面体が5つしかないことを示す：

正 面体の各面は 本の辺に囲まれているが，どの辺も共有されていて2回ずつ数えられる：

正 面体の各面には 個の頂点があるが，頂点は共有されていて 回ずつ数えられる：

オイラー(Euler)の公式 を使って面の数を求めることができる：

この最後の公式がうまく定義されるためには分母が正の整数である必要がある：

したがって，次の5つの場合になる：

これをPolyhedronDataの実際の数と比較する：

幾何学問題  (3)

が真であれば，領域 ℛ は の部分集合である．Disk[{0,0},{2,1}]がRectangle[{-2,-1},{2,1}]の部分集合であることを示す：

これをプロットする：

Cylinder[]⊆Ball[{0,0,0},2]を示す：

これをプロットする：

有限点集合については，点 についてのボロノイ(Voronoi)セルはで定義される．これは， のとき，他のすべての点 より に近いすべての点に相当する．Reduceを使ってボロノイセルの簡単な式を求める：

pts〚1〛に関連するボロノイセルは以下で与えられる：

結果のセルは半空間の交差によって与えられる：

すべてのボロノイセルについての簡単な式を求める：

これらをプロットする：

特性と関係  (10)

簡約の結果はもとの系に等しい：

ToRulesとReplaceRepeatedを使って有限解集合を置換し直すことができる：

Expandを使って簡単な根基を含む置換の結果を簡約する：

代数的数を含む式の簡約にRootReduceを使う：

FindInstanceを使って解の例を求める：

Solveは複雑な方程式の解を置換規則で表す：

Solveはパラメータについての方程式を含む解を除外する：

超越方程式については，Solveがすべての解を与えないことがある：

逆関数を使うとSolveがある種の解を求めるのが速くなる：

完全な解を求めるのには時間がかかり，解自体も長くなることがある：

以下は，x 2が解であるような の値を求める：

SolveAlwaysは複雑な式が常に真であるパラメータの値を返す：

次は，同じ問題をReduceを使って解く：

Resolveは限定子を除去するが，必ずしも結果の限定子を含まない式を解く訳ではない：

Eliminateは複雑な方程式の系から変数を除去する：

以下では同じ問題をResolveを使って解いている：

Reduceは結果の方程式も解く：

考えられる問題  (3)

は不等式に含まれているので，実数だと仮定される． は複素数でもよい：

領域Realsが指定されると，， それにSqrt[x]は実数でなければならなくなる：

以下では不等式の両辺が実数である の値は複素数でもよい：

ReduceはWolfram言語関数の分枝切断線に依存する方程式を解かない：

第1条件が非零である領域をプロットする：

一般に，入力方程式の可除特異点は有効な解とはみなされない：

しかし，解には自動簡約で削除される可除特異点が含まれることがある：

における可除特異点は評価によって削除される：

以下では における可除特異点が方程式の前処理に使われたTogetherによって削除されている：

おもしろい例題  (1)

極限の定義を直接使っての垂直方向の漸近線を求める：

Wolfram Research (1988), Reduce, Wolfram言語関数， https://reference.wolfram.com/language/ref/Reduce.html （2024年に更新）.

テキスト

Wolfram Research (1988), Reduce, Wolfram言語関数， https://reference.wolfram.com/language/ref/Reduce.html （2024年に更新）.

CMS

Wolfram Language. 1988. "Reduce." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Reduce.html.

APA

Wolfram Language. (1988). Reduce. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Reduce.html

BibTeX

@misc{reference.wolfram_2024_reduce, author="Wolfram Research", title="{Reduce}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Reduce.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_reduce, organization={Wolfram Research}, title={Reduce}, year={2024}, url={https://reference.wolfram.com/language/ref/Reduce.html}, note=[Accessed: 21-November-2024 ]}