ReliabilityDistribution
ReliabilityDistribution[bexpr,{{x1,dist1},{x2,dist2},…}]
成分 xiが信頼性分布 distiに従う系の信頼性分布を表す.ただし,系はブール式 bexpr がTrueのときに動いており,成分 xiは xiがTrueのときに動いている.
詳細

- ReliabilityDistribution[bexpr,…]は信頼性ブロック図指定に相当する.
- ブール式 bexpr は系の構造関数としても知られている
- よく使用される構造関数
-
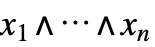
直列の系 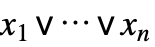
並列の系 ![TemplateBox[{BooleanCountingFunction, paclet:ref/BooleanCountingFunction}, RefLink, BaseStyle -> {2ColumnTableMod}][{k,n},n] TemplateBox[{BooleanCountingFunction, paclet:ref/BooleanCountingFunction}, RefLink, BaseStyle -> {2ColumnTableMod}][{k,n},n]](Files/ReliabilityDistribution.ja/3.png)
k アウトオブ n の系 BooleanConsecutiveFunction[k,n] 連続する k アウトオブ n の系 - 構造関数 bexpr は任意の正ユネイトブール関数でよい.
- UnateQ[bexpr]を使ってブール式が正ユネイトかどうかの検定を行うことができる.
- 成分の信頼性分布 disti は一変量で,PDF[disti,t]が t≤0のときはゼロでなければならない.
- 成分インディケータ変数 xiを持つReliabilityDistribution[bexpr,…]
-
xiTrue 成分 xi が動いていることを示す xiFalse 成分 xi が故障したことを示す - 時間 t におけるReliabilityDistribution[bexpr,{{x1,dist1},…}]の生存関数はProbability[bexpr/.{x1->t1>t,…},{t1disti,…}]で与えられる.
- ReliabilityDistributionは,Mean,SurvivalFunction,HazardFunction,RandomVariate等の関数とともに使うことができる.
例題
すべて開くすべて閉じる例 (3)
スコープ (26)
基本的な用法 (4)
3つの成分のうち2つが動いている必要がある系のSurvivalFunctionを求める:
構造関数 (7)
パラメトリック寿命分布 (5)
ノンパラメトリック寿命関数 (3)
航空機のガラスの強度をSmoothKernelDistributionを使ってモデル化する:
HistogramDistributionを使って成分をモデル化する:
EmpiricalDistributionを使ってデータから成分を直接モデル化する:
派生寿命分布 (7)
StandbyDistributionで成分をモデル化する:
SurvivalFunctionをプロットする:
StandbyDistributionで成分をモデル化する:
ParameterMixtureDistributionに従う系:
MixtureDistributionで2成分の冷待機の系をモデル化する:
これをReliabilityDistributionで使って生存関数を計算する:
StandbyDistributionとの等価性を示す:
OrderDistributionを使って成分の寿命をモデル化することができる:
SurvivalFunctionをプロットする:
MarginalDistributionを使って成分の寿命をモデル化することができる:
SurvivalFunctionをプロットする:
アプリケーション (12)
航空機の離陸をモデル化する.格納扉は電動,手動のどちらで開くこともできる:
さらに2つのポンプを信頼できる電池を使って動かすことができる.したがって次の燃料移送構造となる:
1時間あたりの故障率を含む分布を定義する.電源の故障率を変数とする:
故障率 ![]() が1時間あたり
が1時間あたり![]() から低下した場合の信頼性の変化を見る:
から低下した場合の信頼性の変化を見る:
小さい電子加速器の真空装置には20個の真空バルブが円形に並んでいる.隣り合った真空バルブが少なくとも3つ故障すると,真空装置は故障する:
衛星には太陽電池パネルで充電される電池からの動力が必要である.系が持ちこたえる荷電サイクルの数を計算する:
車輪のそれぞれにボールベアリングが付いたスケートボードについて考える.そのようなスケートボードの寿命を求める:
スケードボードは4つの車のうち3つが動けば使うことができると仮定する:
車を運転するためには4つのタイヤすべてが必要である.タイヤの寿命分布はExponentialDistribution[0.0004]で与えられるとして,その車のタイヤについての故障率と故障までの平均時間を計算する:
航空機が飛ぶためには,両翼,両翼にある2つのエンジンのどちらか1つ,空気制御装置が必要である.エンジン系をモデル化する:
航空機が300時間のフライト後さらに200時間フライトを行っても航行可能である確率を求める:
あるデータセンターでは,20基のサーバ,1つの電力供給,1つの冷却装置,1つのネットワーク接続が必要である.電力供給には待機成分がある.ネットワーク接続は2つの並列接続からなっている.サーバをモデル化する:
StandbyDistributionで電力供給をモデル化する:
この系が5日間確率0.9995で稼働するための故障率 ![]() の必要条件を求める:
の必要条件を求める:
太陽電池パネルは光電池の配列からなっている.各配列に10個の電池がある:
太陽電池パネルが稼働するためには5つの配列のうち3つとインバータが必要である:
太陽電池パネルを販売する会社は10年保証を提供している.この保証期間は10年延長することができる.会社がこの延長分の保証期間の値段をどのように付けるべきかを求める:
ある物流会社では,物品を顧客まで配達するために,トラック,船舶,列車を使っている.路上輸送のためには3台のトラックのうち2台が必要であり,道路状態もよくなければならない.海上輸送のためには船が運航可能であり天候にも恵まれる必要がある.列車での輸送には運行可能な列車と線路が必要である.路上輸送をモデル化する:
この会社では配達の信頼性を改善するために航空機を1機リースすることを考えている.この航空機が故障までの平均時間をどの程度改善するか計算する:
チャールズ・リンドバーグはパリ・ニューヨーク間の飛行の際にエンジンが1つの航空機と2つの航空機のどちらかを選ぶことができたと仮定する.どちらのエンジン構造が信頼性が高いかを調べる:
最良の選択肢は2つのエンジンを並列接続したものであるのは明らかであるが,これはリンドバーグの飛行のときに存在しなかったため,彼はエンジン1つの選択肢を選ぶしかなかった.1つのエンジンで33.5時間の飛行を行うことができる確率を計算する:
特性と関係 (14)
ReliabilityDistributionは入力変数に局所名を使う:
同一成分の直列接続はOrderDistributionに相当する:
同一成分の並列接続はOrderDistributionに相当する:
![]() アウトオブ
アウトオブ ![]() の系はRankedMin関数を伴うTransformedDistributionに相当する:
の系はRankedMin関数を伴うTransformedDistributionに相当する:
Weibull寿命分布に従う成分の直列の系もまたWeibull分布に従う:
ReliabilityDistributionは系が動くためには成分 ![]() または
または ![]() が動かなければならないことをモデル化する:
が動かなければならないことをモデル化する:
対応するFailureDistributionは ![]() と
と ![]() の両方が故障する事象をモデル化する:
の両方が故障する事象をモデル化する:
成分 ![]() または
または ![]() が動いていることは
が動いていることは ![]() と
と ![]() の両方が故障する事象に相当する:
の両方が故障する事象に相当する:
系が動くためには4つの成分のうち2つが動くことが必要な場合をモデル化する:
これは系が故障するためには4つの成分のうち3つが故障する必要がある場合と等しい:
ReliabilityDistribution[f[x1,…],…]FailureDistribution[¬f[¬x1,…],…]:
SystemModelのReliabilityDistributionを信頼性情報とともに取り出す:
考えられる問題 (3)
TruncatedDistributionを使って領域を正の値のみに制限する:
ReliabilityDistributionは正ユネイト構造の式に対してのみうまく定義することができる:
UnateQを使ってブール式が正ユネイトかどうかの検定を行う:
おもしろい例題 (2)
最高で4つまでの同一成分があるすべての系のハザード関数を示す:
Graphを信頼度ブロック線図として使用する:
テキスト
Wolfram Research (2012), ReliabilityDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/ReliabilityDistribution.html.
CMS
Wolfram Language. 2012. "ReliabilityDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ReliabilityDistribution.html.
APA
Wolfram Language. (2012). ReliabilityDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ReliabilityDistribution.html