ReliabilityDistribution[bexpr,{{x1,dist1},{x2,dist2},…}]
表示一个系统的可靠性分布,其中元件 xi 具有可靠性分布 disti,当布尔表达式 bexpr 为 True,整个系统工作;当 xi 为 True,元件 xi 工作.


ReliabilityDistribution
ReliabilityDistribution[bexpr,{{x1,dist1},{x2,dist2},…}]
表示一个系统的可靠性分布,其中元件 xi 具有可靠性分布 disti,当布尔表达式 bexpr 为 True,整个系统工作;当 xi 为 True,元件 xi 工作.
更多信息

- ReliabilityDistribution[bexpr,…] 对应于可靠性框图规范.
- 布尔表达式 bexpr 也称之为系统的结构函数.
- 典型的结构函数包括:
-
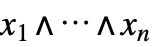
串联系统 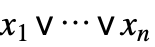
并联系统 ![TemplateBox[{BooleanCountingFunction, paclet:ref/BooleanCountingFunction}, RefLink, BaseStyle -> {2ColumnTableMod}][{k,n},n] TemplateBox[{BooleanCountingFunction, paclet:ref/BooleanCountingFunction}, RefLink, BaseStyle -> {2ColumnTableMod}][{k,n},n]](Files/ReliabilityDistribution.zh/3.png)
k-n 系统 BooleanConsecutiveFunction[k,n] 连续的 k-n 系统 - 结构函数 bexpr 可以是任何正单边(unate)布尔函数.
- UnateQ[bexpr] 可用于检验布尔表达式是否为正单边(unate).
- 元件可靠性分布 disti 需要 PDF[disti,t] 为单变量分布,且当 t≤0 时为0.
- 对于具有元件指示器变量 xi 的 ReliabilityDistribution[bexpr,…]:
-
xiTrue 表明元件 xi 工作 xiFalse 表明元件 xi 失效 - 对于 ReliabilityDistribution[bexpr,{{x1,dist1},…}] 在时间 t 的生存函数由 Probability[bexpr/.{x1->t1>t,…},{t1disti,…}] 给定.
- ReliabilityDistribution 可与函数 Mean、SurvivalFunction、HazardFunction 和 RandomVariate 一起使用.
范例
打开所有单元 关闭所有单元范围 (26)
基本用途 (4)
求3个元件中2个工作的系统的 SurvivalFunction:
结构函数 (7)
使用 UnateQ 检验布尔表达式是否为正单边(unate):
参数寿命分布 (5)
使用任何包括 LogNormalDistribution 的参数寿命分布:
绘制 SurvivalFunction 图线:
非参数寿命分布 (3)
使用 SmoothKernelDistribution 模拟飞机玻璃的强度:
用 HistogramDistribution 模拟元件:
直接从具有 EmpiricalDistribution 的数据中模拟元件:
导出的寿命分布 (7)
用 StandbyDistribution 模拟一个元件:
绘制 SurvivalFunction:
用 StandbyDistribution 模拟一个元件:
具有 ParameterMixtureDistribution 的系统:
模拟具有 MixtureDistribution 的两元件冷备用系统:
在 ReliabilityDistribution 中使用并计算生存函数:
显示与 StandbyDistribution 的等价:
OrderDistribution 可用于模拟元件寿命:
绘制 SurvivalFunction:
MarginalDistribution 可用于模拟元件寿命:
绘制 SurvivalFunction:
应用 (12)
小的电子加速器中真空系统包含 20 个排成圆圈的真空灯泡. 如果至少三个邻接的真空灯泡失效,则真空系统会失效:
卫星需要由太阳能电池板充电的电池供电. 计算系统能够经得起考验的负载周期数:
汽车有四个均要驾驶的轮胎. 给出轮胎的寿命分布为 ExponentialDistribution[0.0004],计算关于轮胎的汽车的失效率和失效平均时间:
为了飞行,飞机需要两个机翼,每个机翼上两个引擎中的一个以及空气控制系统操控. 模拟该引擎系统:
数据中心需要20台服务器,一个电源,一个冷却系统和一个网络连接. 电源有一个备份. 网络连接由两个并联连接组成. 模拟服务器:
用 StandbyDistribution 模拟电源:
销售太阳能电池板的公司提供10年的保证. 可以再添加10年. 求公司应如何给延长的保质期定价:
一家物流公司使用车、船和火车将货物交付给客户. 道路运输需要两三辆卡车和明确的道路路线. 船运需要正常运作的船舶和平静的天气条件,铁运需要一个正常运作的列车和轨道. 模拟道路运输:
公司考虑租赁一架飞机以改善分发的可靠性. 计算飞机能改善多少故障的平均时间:
假设 Charles Lindbergh 在纽约和巴黎之间可以选择一个或两个引擎的飞机. 调查哪个引擎的配置可以给出最高的可靠性:
最佳选择是并联两种引擎,但是这在当时不可行,因此 Lindbergh 选择一个引擎. 计算一个引擎存活33.5个小时飞行的概率:
属性和关系 (14)
在输入中,ReliabilityDistribution 使用变量的局部名称:
同样元件的串联连接对应于 OrderDistribution:
同样元件的并联连接对应于 OrderDistribution:
![]() -
-![]() 系统对应于具有 RankedMin 函数的 TransformedDistribution:
系统对应于具有 RankedMin 函数的 TransformedDistribution:
ReliabilityDistribution 模拟元件 ![]() 或
或 ![]() 必须工作,系统才会工作:
必须工作,系统才会工作:
对应的 FailureDistribution 模拟 ![]() 和
和 ![]() 均有故障的事件:
均有故障的事件:
ReliabilityDistribution[f[x1,…],…]FailureDistribution[¬f[¬x1,…],…]:
为带有可靠性信息的 SystemModel 提取 ReliabilityDistribution:
可能存在的问题 (3)
使用 TruncatedDistribution 限制域只为正值:
ReliabilityDistribution 只对正单边(unate)结构表达式有定义:
使用 UnateQ 检验布尔表达式是否为正单边(unate):
巧妙范例 (2)
使用 Graph 作为可靠性方框图:
文本
Wolfram Research (2012),ReliabilityDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ReliabilityDistribution.html.
CMS
Wolfram 语言. 2012. "ReliabilityDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ReliabilityDistribution.html.
APA
Wolfram 语言. (2012). ReliabilityDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ReliabilityDistribution.html 年
BibTeX
@misc{reference.wolfram_2025_reliabilitydistribution, author="Wolfram Research", title="{ReliabilityDistribution}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/ReliabilityDistribution.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_reliabilitydistribution, organization={Wolfram Research}, title={ReliabilityDistribution}, year={2012}, url={https://reference.wolfram.com/language/ref/ReliabilityDistribution.html}, note=[Accessed: 07-February-2026]}