SurfaceIntegrate

SurfaceIntegrate[f,{x,y,…}∈surface]

computes the scalar surface integral of the function f[x,y,…] over the surface.

SurfaceIntegrate[{p,q,…},{x,y,…}∈surface]

computes the vector surface integral of the vector field {p[x,y,…],q[x,y,…],…}.

Details and Options

  • Surface integrals are also known as flux integrals.
  • Scalar surface integrals integrate scalar functions over a hypersurface. They are typically used to compute things like area, mass and charge for a surface.
  • Vector surface integrals are used to compute the flux of a vector function through a surface in the direction of its normal. Typical vector functions include a fluid velocity field, electric field and magnetic field.
  • The scalar surface integral of a function f over a surface 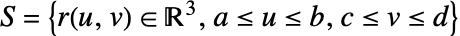is given by:
  • where TemplateBox[{{{{partial, _, u}, {r, (, {u, ,, v}, )}}, x, {{partial, _, v}, {r, (, {u, ,, v}, )}}}}, Norm] is the measure of a parametric surface element.
  • The scalar surface integral of f over a hypersurface 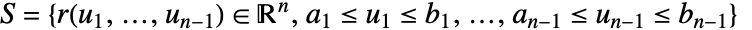is given by:

  • The scalar surface integral is independent of the parametrization and orientation of the surface. Any 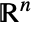dimensional RegionQ object in 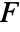can be use for the surface.
  • The vector surface integral of a vector function 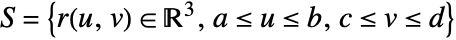over a surface 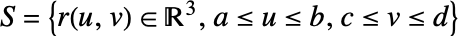is given by:
  • where 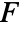F(r(u,v)).(partial_tr(u,v)xpartial_sr(u,v)) is the projection of the vector function 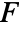onto the normal direction so only the component in the normal direction gets integrated.
  • The vector surface integral of 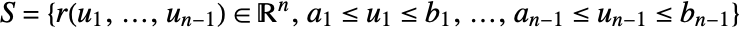over a a hypersurface 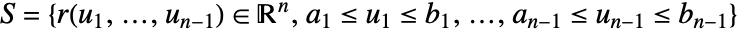is given by:

  • The vector surface integral is independent of the parametrization, but depends on the orientation.
  • The orientation for a hypersurface is given by a normal vector field 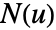over the surface.
  • For a parametric hypersurface ParametricRegion[{r1[u1,…,un-1],…,rn[u1,…,un-1]},…], the normal vector field 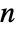is taken to be Cross[∂u1r[u],…,∂un-1r[u]].
  • The RegionQ objects in Wolfram Language are not oriented. However for the convenience of this function, you can assume the following rules for getting oriented hypersurfaces.
  • For solid (of dimension 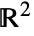) and bounded RegionQ objects ℛ, take the surface to be the region boundary (RegionBoundary[ℛ]) and the normal orientation to be pointed outward.
  • Special solids in with their assumed boundary surface (edge) normal orientation include:
  • Triangleoutward normal
    Rectangleoutward normal
    Polygonoutward normal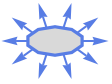
    Diskoutward normal
    Ellipsoidoutward normal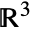
    Annulusoutward normal
  • Special solids in with their assumed boundary surface (face) normal orientation include:
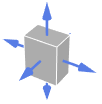
  • Tetrahedronoutward normal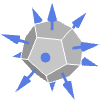
    Cuboidoutward normal
    Polyhedronoutward normal
    Balloutward normal
    Ellipsoidoutward normal
    Cylinderoutward normal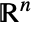
    Coneoutward normal
  • Special solids in 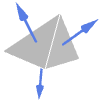with their assumed surface (facet) and normal orientation:
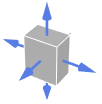
  • Simplexoutward normal
    Cuboidoutward normal
    Balloutward normal
    Ellipsoidoutward normal
  • The following options can be given:
  • Assumptions $Assumptionsassumptions to make about parameters
    GenerateConditions Automaticwhether to generate answers that involve conditions on parameters
    WorkingPrecision Automaticthe precision used in internal computations
  • SurfaceIntegrate uses a combination of symbolic and numerical methods when the input involves inexact quantities.

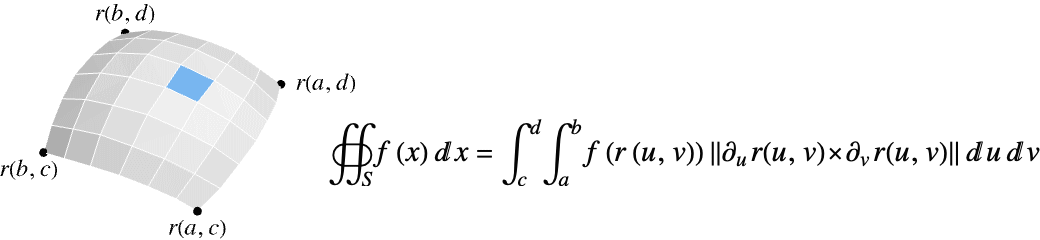
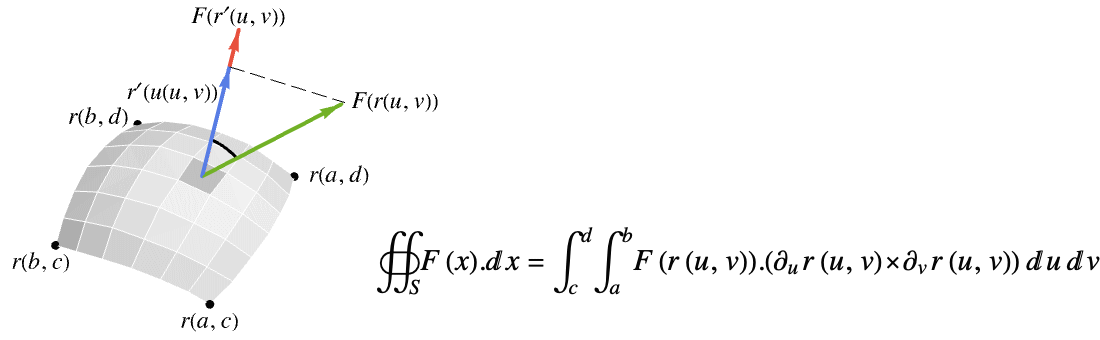
Examples

open allclose all

Basic Examples  (6)

Surface integral of a scalar function over a spherical surface:

Surface integral of a vector field over a spherical surface:

Surface integral of a scalar field over a parametric surface:

Surface integral of a vector field over a parametric surface:

Surface integral of a scalar field over a surface:

Visualize the scalar field on the surface:

Surface integral of a vector field over a surface:

Visualize the scalar field on the surface:

Scope  (32)

Basic Uses  (5)

Surface integral of a scalar field over a sphere in three dimensions:

Surface integral of a vector field in three dimensions:

SurfaceIntegrate works with many special surfaces:

Surface integral over a parametric surface:

SurfaceIntegrate works in dimensions different from three:

Scalar Functions  (5)

Surface integral of a scalar field over a three-dimensional surface:

Plot of the surface:

Surface integral:

Surface integral of a scalar field:

The surface integral:

Surface integral of a scalar field in three dimensions over a sphere:

Surface integral of a scalar field over the surface of a pyramid:

Surface integral:

Surface integral of a scalar field over a parametric surface in three dimensions:

The surface and its plot:

Vector Functions  (5)

Surface integral of a vector field in three dimensions over a sphere:

Visualize the vector field on the surface:

Surface integral:

Surface integral of a vector field in three dimensions over a triangle:

Surface integral:

Surface integral of a vector field over a parametric surface in three dimensions:

Surface integral of a vector field over the boundary of an ellipsoid:

Surface integral of a vector field in three dimensions over the boundary of a cone:

Visualization of the vector field on the surface:

Surface integral:

Special Surfaces  (10)

Surface integral of a vector field over a sphere of radius :

Surface integral of a vector field over the boundary of a cube of side centered at the origin:

Surface integral of a vector field over the boundary of a tetrahedron:

Surface integral of a vector field over a triangle:

Surface integral of a vector field over an ellipsoid:

Surface integral of a vector field over the boundary of a cone:

Surface integral of a vector field over the boundary of a cylinder:

Surface integral of a vector field over the boundary of a parallelepiped:

Surface integral of a vector field over the boundary of a prism:

Surface integral over a polygon in three dimensions:

The orientation of the polygon depends on the order in which the points are given:

Parametric Surfaces  (4)

Surface integral of a vector field over a parametric surface:

Surface integral of a vector field over a parametrized dome-like surface:

Surface integral over a parametrized cylinder:

Surface integral of a vector field over a parametrized hyperboloid:

Hypersurfaces  (3)

Surface integral over a 1D hypersurface in 2D:

Surface integral over a 3D hypersurface in 4D:

Volume of a five-dimensional sphere, computed using a surface integral:

Options  (4)

Assumptions  (1)

Assumptions can be specified for symbolic parameters:

With Assumptions, a result valid under the given assumptions is given:

GenerateConditions  (1)

SurfaceIntegrate can work with symbolic parameters:

Generate conditions on the parameters:

WorkingPrecision  (2)

If a WorkingPrecision is specified, a numerical result is given:

The result has finite precision if the integrand has a finite precision:

Applications  (18)

College Calculus  (5)

Surface integral over the boundary of a cube of side 2 centered at the origin:

Surface integral over a paraboloid:

Surface integral over the side of a cylinder:

Surface integral over a hemispherical shell of radius :

Surface integral over the boundary of a cube:

Areas  (3)

Area of a sphere:

Area of an ellipsoid:

Area of a triangle:

Volumes  (3)

Volume of an ellipsoid computed using a surface integral:

Volume of a icosahedron computed using a surface integral:

Volume of a cube of side computed using a surface integral:

Flux  (3)

Flux of the electric field generated by a point charge at the origin over a sphere surrounding it:

Flux of the uniform magnetic field of an infinite solenoid with windings per unit length traversed by a current over a disk orthogonal to it:

Electric field due to an infinite charged wire of linear charge density :

Flux across a cylinder of height and radius having the axis on the charged wire:

Centroids  (2)

Mass of a hemispherical shell of unit density and radius :

coordinate of the center of mass:

coordinate of the center of mass:

coordinate of the center of mass:

Moments of inertia of a thin cut cone:

About the axis:

About the axis:

About the axis:

Classical Theorems  (2)

Compute the Curl of a vector field :

The surface integral of over an open surface is:

This is the same as the line integral of over the boundary of the surface:

Compute the surface integral of a vector field over a closed surface:

This is the same as the integral of Div[f] over the interior of the surface:

Properties & Relations  (5)

Apply N[SurfaceIntegrate[...]] to obtain a numerical solution if the symbolic calculation fails:

Find the center of mass of a thin triangular surface of unit mass per unit area:

Find the total mass:

Find the component of the center of mass:

Find the component of the center of mass:

Find the component of the center of mass:

The center of mass can also be obtained using RegionCentroid:

Find the moment of inertia around the axis of a thin cylindrical shell of unit area density:

The answer can also be computed with MomentOfInertia:

Find the area of a tetrahedron:

The answer can also be computed with Area:

Find the volume of a icosahedron:

The answer can also be computed with Volume:

Neat Examples  (9)

Volume of a pseudosphere computed using a surface integral:

Plot of a finite part of the pseudosphere:

Volume of a drop-shaped solid using a surface integral:

Volume of a Dupin cyclide:

Flux of a vector field across a part of a Bohemian dome:

Surface integral of a vector field over a portion of a conocuneus of Wallis:

Surface integral of a vector field over a funnel-shaped surface:

Area of a Gaudi surface:

Compute numerically the area of Guimard's surface:

Surface integral of a vector field over a neiloid:

Wolfram Research (2023), SurfaceIntegrate, Wolfram Language function, https://reference.wolfram.com/language/ref/SurfaceIntegrate.html.

Text

Wolfram Research (2023), SurfaceIntegrate, Wolfram Language function, https://reference.wolfram.com/language/ref/SurfaceIntegrate.html.

CMS

Wolfram Language. 2023. "SurfaceIntegrate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SurfaceIntegrate.html.

APA

Wolfram Language. (2023). SurfaceIntegrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SurfaceIntegrate.html

BibTeX

@misc{reference.wolfram_2024_surfaceintegrate, author="Wolfram Research", title="{SurfaceIntegrate}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/SurfaceIntegrate.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_surfaceintegrate, organization={Wolfram Research}, title={SurfaceIntegrate}, year={2023}, url={https://reference.wolfram.com/language/ref/SurfaceIntegrate.html}, note=[Accessed: 30-December-2024 ]}