SurfaceIntegrate

SurfaceIntegrate[f,{x,y,…}∈surface]

计算函数 f[x,y,…] 在 surface 上的标量曲面积分.

SurfaceIntegrate[{p,q,…},{x,y,…}∈surface]

计算向量场 {p[x,y,…],q[x,y,…],…} 的向量曲面积分.

更多信息和选项

  • 曲面积分亦称为通量积分.
  • 标量曲面积分对超曲面上的标量函数进行积分. 它们通常用于计算曲面的面积、质量和电荷.
  • 向量曲面积分用于计算向量函数在曲面法线方向上的通量. 典型的向量函数包括流体速度场、电场和磁场.
  • 函数 f 在 surface 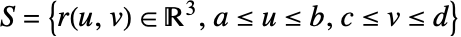上的标量曲面积分由下式给出：
  • 其中，TemplateBox[{{{{partial, _, u}, {r, (, {u, ,, v}, )}}, x, {{partial, _, v}, {r, (, {u, ,, v}, )}}}}, Norm] 是参数化曲面元素的度量.
  • f 在超曲面 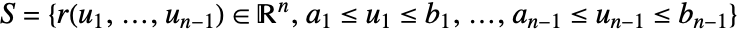上的标量曲面积分由下式给出：

  • 标量曲面积分与 surface 的参数化和方位无关. surface 可以是 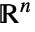中的任意 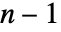维的 RegionQ 对象.
  • 向量函数 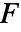在 surface 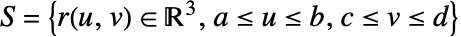上的向量曲面积分由下式给出：
  • 其中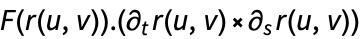，F(r(u,v)).(partial_tr(u,v)xpartial_sr(u,v)) 是向量函数 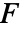在法线方向上的投影，所以只对法线方向的分量进行积分.
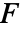  • 在超曲面 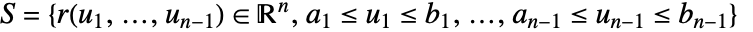上的向量曲面积分由下式给出：

  • 向量曲面积分与参数化无关，取决于方位.
  • 超曲面的方位由曲面上的法向量场 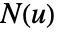给出.
  • 对于参数化超曲面 ParametricRegion[{r1[u1,…,un-1],…,rn[u1,…,un-1]},…]，法向量场 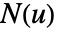为 Cross[∂u1r[u],…,∂un-1r[u]].
  • Wolfram 语言中的 RegionQ 对象是没有方向的. 但是，为方便起见，可以假定以下规则来获取定向超曲面.
  • 对于维度为 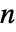的立体和有界 RegionQ 对象 ℛ，将区域的边界 (RegionBoundary[ℛ]) 视为曲面，将向外的方向视为法线方向.
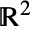  • 中具有假定边界曲面（边）法线方向的特殊立体包括：
  • Triangle外向法线
    Rectangle外向法线
    Polygon外向法线
    Disk外向法线
    Ellipsoid外向法线
    Annulus外向法线
  • 中具有假定边界曲面（面）法线方向的特殊立体包括：
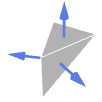
  • Tetrahedron外向法线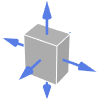
    Cuboid外向法线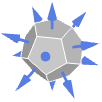
    Polyhedron外向法线
    Ball外向法线
    Ellipsoid外向法线
    Cylinder外向法线
    Cone外向法线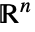
  • 中具有假定曲面（面）的特殊立体及其法线方向：
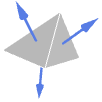
  • Simplex外向法线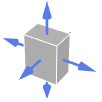
    Cuboid外向法线
    Ball外向法线
    Ellipsoid外向法线
  • 可给出以下选项：
  • Assumptions $Assumptions关于参数的假设
    GenerateConditions Automatic是否给出与参数的条件有关的答案
    WorkingPrecision Automatic内部计算使用的精度
  • 当输入涉及不精确的量时，SurfaceIntegrate 将符号法和数值法结合起来使用.

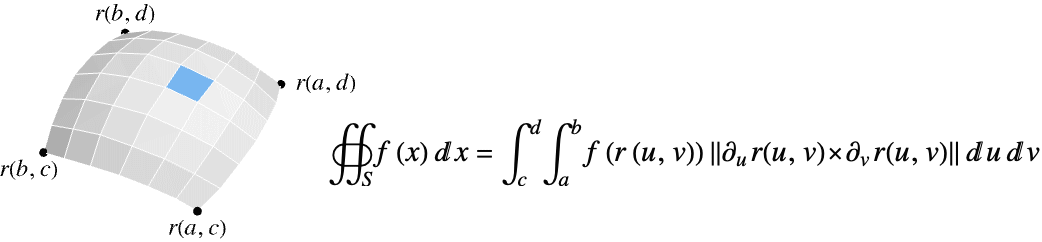
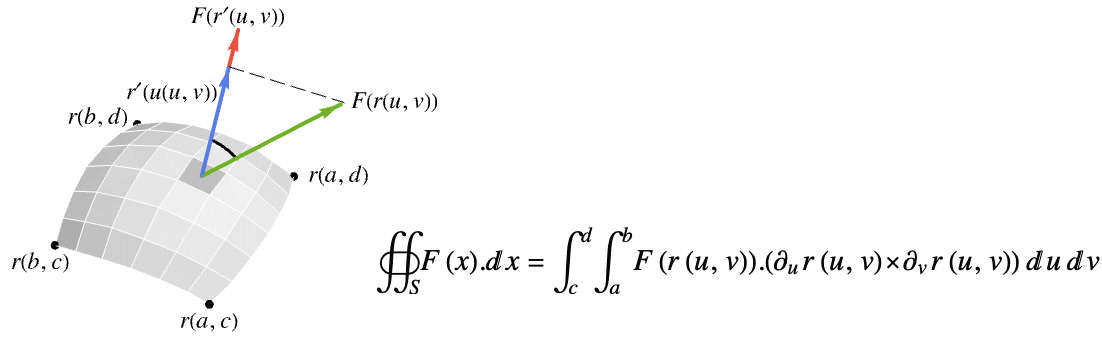
范例

打开所有单元关闭所有单元

基本范例  (6)

标量函数在球面上的曲面积分：

向量场在球面上的曲面积分：

标量场在参数化曲面上的曲面积分：

向量场在参数化曲面上的曲面积分：

标量场在曲面上的曲面积分：

可视化曲面上的标量场：

向量场在曲面上的曲面积分：

可视化曲面上的向量场：

范围  (32)

基本用法  (5)

标量场在三维球面上的曲面积分：

向量场在三维空间的曲面积分：

SurfaceIntegrate 适用于许多特殊曲面：

参数化曲面上的曲面积分：

SurfaceIntegrate 适用于三维以外的维度：

标量函数  (5)

标量场在三维曲面上的曲面积分：

曲面：

曲面积分：

标量场的曲面积分：

曲面积分：

标量场在球面上的曲面积分：

标量场在金字塔表面上的曲面积分：

曲面积分：

标量场在三维参数化曲面上的曲面积分：

曲面：

向量函数  (5)

向量场在三维球面上的曲面积分：

可视化曲面上的向量场：

曲面积分：

三维空间中向量场在三角形的曲面积分：

曲面积分：

向量场在三维参数化曲面上的曲面积分：

向量场在椭球边界上的曲面积分：

三维空间中向量场在圆锥表面上的曲面积分：

可视化曲面上的向量场：

曲面积分：

特殊曲面  (10)

向量场在半径为 的球面上的曲面积分：

向量场在以原点为中心、边长为 的立方体的边界上的曲面积分：

向量场在四面体边界上的曲面积分：

向量场在三角形上的曲面积分：

向量场在椭球上的曲面积分：

向量场在圆锥表面上的曲面积分：

向量场在圆柱表面上的曲面积分：

向量场在平行六面体表面上的曲面积分：

向量场在棱柱体表面上的曲面积分：

三维空间中多边形上的曲面积分：

多边形的方位取决于给出点的顺序：

参数化曲面  (4)

向量场在参数化曲面上的曲面积分：

向量场在参数化圆顶状曲面上的曲面积分：

参数化圆柱体上的曲面积分：

向量场在参数化双曲面上的曲面积分：

超曲面  (3)

二维空间中一维超曲面上的曲面积分：

四维空间中三维超曲面上的曲面积分：

用曲面积分计算五维球面的体积：

选项  (4)

Assumptions  (1)

可为符号参数指定假设：

有 Assumptions 的情况下，会给出在给定假设下有效的结果：

GenerateConditions  (1)

SurfaceIntegrate 适用于符号参数：

生成关于参数的条件：

WorkingPrecision  (2)

如果指定了 WorkingPrecision，则给出数值结果：

如果被积函数的精度有限，则结果的精度有限：

应用  (18)

大学微积分  (5)

以原点为中心的、边长为 2 的立方体的边界上的曲面积分：

抛物面上的曲面积分：

圆柱体侧面的曲面积分：

半径为 的半球壳上的曲面积分：

立方体边界上的曲面积分：

面积  (3)

球面的面积：

椭球的面积：

三角形的面积：

体积  (3)

用曲面积分计算的椭球的体积：

用曲面积分计算的二十面体的体积：

用曲面积分计算的边长为 的立方体的体积：

通量  (3)

原点处的点电荷 在围绕它的球面上产生的电场通量：

无限螺线管的均匀磁场的通量，每单位长度上有 个绕组，电流 在与其正交的圆盘上穿过：

线电荷密度为 的无限带电导线产生的电场：

穿过高度为 、半径为 的圆柱体的电通量，圆柱体的轴即为带电导线：

质心  (2)

单位密度和半径为 的半球壳的质量：

质心的 坐标：

质心的 坐标：

质心的 坐标：

薄切圆锥的惯性矩：

关于 轴的：

关于 轴的：

关于 轴的：

经典定理  (2)

计算向量场 的 Curl，即 ：

在开放曲面上的曲面积分为：

这与 在曲面边界上的线积分相同：

计算向量场 在闭合曲面上的曲面积分：

这与 Div[f] 在曲面内部的积分相同：

属性和关系  (5)

如果符号计算失败，用 N[SurfaceIntegrate[...]] 获取数值解：

求单位面积上具有单位质量的薄三角形曲面的质心：

求总质量：

求质心的 分量：

求质心的 分量：

求质心的 分量：

也可用 RegionCentroid 获取质心：

求具有单位面积密度的薄圆柱壳绕 轴的惯性矩：

也可用 MomentOfInertia 算出答案：

求四面体的面积：

也可用 Area 算出答案：

求二十面体的体积：

也可用 Volume 算出答案：

巧妙范例  (9)

用曲面积分计算伪球体的体积：

绘制伪球体的有限部分：

使用曲面积分计算水滴形物体的体积：

Dupin 四次圆纹曲面的体积：

向量场穿过部分 Bohemian 圆顶的通量：

向量场在部分 conocuneus of Wallis 上的曲面积分：

向量场在漏斗形曲面上的曲面积分：

Gaudi 曲面的面积：

用数值法计算 Guimard 曲面的面积：

向量场在 Neiloid 上的曲面积分：

Wolfram Research (2023)，SurfaceIntegrate，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SurfaceIntegrate.html.

文本

Wolfram Research (2023)，SurfaceIntegrate，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SurfaceIntegrate.html.

CMS

Wolfram 语言. 2023. "SurfaceIntegrate." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SurfaceIntegrate.html.

APA

Wolfram 语言. (2023). SurfaceIntegrate. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SurfaceIntegrate.html 年

BibTeX

@misc{reference.wolfram_2024_surfaceintegrate, author="Wolfram Research", title="{SurfaceIntegrate}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/SurfaceIntegrate.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_surfaceintegrate, organization={Wolfram Research}, title={SurfaceIntegrate}, year={2023}, url={https://reference.wolfram.com/language/ref/SurfaceIntegrate.html}, note=[Accessed: 05-November-2024 ]}