TriangularDistribution

TriangularDistribution[{min,max}]

min と max の間の値を与える対称の統計的三角分布を表す．

TriangularDistribution[]

0と1の間の値を与える対称の統計的三角分布を表す．

TriangularDistribution[{min,max},c]

c で最頻値となる三角分布を表す．

詳細

予備知識

  • TriangularDistribution[{min,max},c]は，区間 min≤x≤max でサポートされ，サポートの下端点，サポートの上端点，その最頻値の 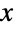座標をそれぞれを指定する3つの実数 min，max，c (min<c<max)でパラメータ化された連続統計分布を表す．一般に，三角分布のPDFは三角（区間線形，下に凹，単峰性）で単一の「峰」（大域的最大値）を持つ．その全体的な形（高さ，広がり，最大値の水平位置）は min，max，c の値で決定される．母数が1つの形TriangularDistribution[{min,max}]は 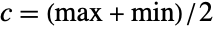についてTriangularDistribution[{min,max},c]に等しく，母数がない形TriangularDistribution[]はTriangularDistribution[{0,1},1/2]に等しい．対称の三角分布は尖叉分布と呼ばれることがある．
  • 三角分布は，近年では1930年代の中頃にはじめて扱われているが，18世紀の英国の研究者Thomas Simpsonの業績まで遡ることができる．歴史的には，この分布は他の分布でモデル化された変量に関連した，あるいはそこから派生した確率的な数量をモデル化するツールとして使われてきた．（例えば，三角分布は2つの一様確率変量の平均をモデル化する分布である．）しかし，近年では，三角分布はさまざまな分野のモデル化に使われている．例えば，三角分布はプロジェクトの評価や審査技術を扱うさまざまな文献で中心的に扱われている．この分布は，モンテカルロシミュレーションでよく使われるツールであり，離散系のシミュレーション，不確実性と機械学習，金融，サプライチェーンの管理等の分野における現象のモデル化に使われてきている．
  • RandomVariateを使って，三角分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,TriangularDistribution[{min,max},c]]（より簡略な表記では xTriangularDistribution[{min,max},c]）を使って，確率変数 x が三角分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 確率密度関数および累積分布関数は，PDF[TriangularDistribution[{min,max},c],x]およびCDF[TriangularDistribution[{min,max},c],x]を使って得られることがある．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って，与えられたデータ集合が三角分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからパラメトリック三角分布を推定することが，FindDistributionParametersを使ってデータを三角分布にフィットすることができる．ProbabilityPlotを使って記号三角分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号三角分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換された三角分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使って三角分布を含む高次元分布を構築することが，ProductDistributionを使って三角分布を含む独立成分分布の結合分布を計算することができる．
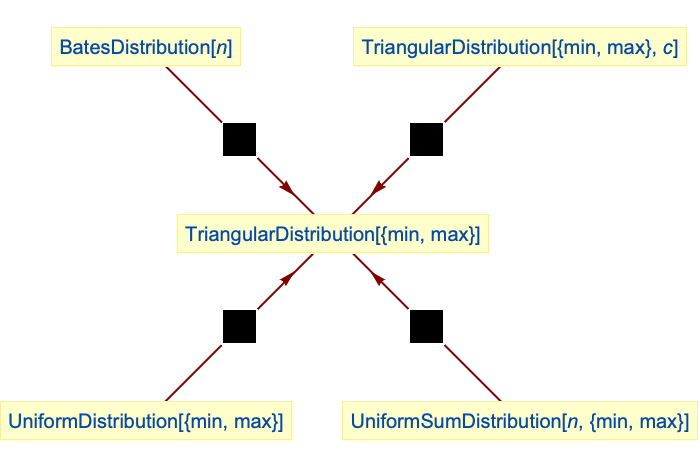
  • TriangularDistributionは，他の数多くの分布と関連している．2つの一様変数の平均はTriangularDistributionに従うので，UniformSumDistribution[2,{min,max}]およびUniformSumDistribution[2,{min,max}]の2つの分布は比例特性関数(CharacteristicFunction)にを持つ．TriangularDistributionは，TriangularDistribution[]の特性関数が厳密にBatesDistribution[2]の特性関数であるという意味で，BatesDistributionで一般化され，UniformDistribution，VonMisesDistribution，LogisticDistribution，WeibullDistribution，LaplaceDistribution，ChiSquareDistributionとも密接な関係がある．

例題

すべて開くすべて閉じる

例  (4)

確率密度関数：

累積分布関数：

平均と分散：

中央値：

スコープ  (8)

三角分布から乱数のサンプルを生成する：

そのヒストグラムを確率密度関数と比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

歪度は形状母数 c にともなって変化する：

対称の場合歪度は0である：

尖度は定数である：

母数の関数としての閉形式の種々のモーメント：

Moment：

Momentは閉形式である：

CentralMoment：

記号次数の閉形式：

FactorialMoment：

Cumulant：

ハザード関数：

分位関数：

母数でQuantityを一貫して使うとQuantityDistributionが与えられる：

密度の分散を求める：

アプリケーション  (2)

重役が100万単位の製品の過去における季節的需要についての説明を受けた．最低需要，最高需要，最尤需要はそれぞれ1，1.4，1.25である．TriangularDistributionを使って予想需要とその標準偏差を求める：

シンクロトロン光線からの二次粒子の推進力はTriangularDistributionでモデル化することができる：

この分布は対称で で最大に達する：

高さの半分における分布密度のモーメントを求める：

半値幅を求める：

特性と関係  (6)

三角分布は平行移動と正の因子によるスケーリングの下では閉じている：

他の分布との関係：

2つの一様変数の平均はTriangularDistributionになる：

三角分布はBatesDistributionの特殊ケースである：

ArcSinDistributionはTriangularDistributionを変換したものである：

c のデフォルト位置はサポートされている区間の中央である：

考えられる問題  (2)

TriangularDistributionは，min または max が実数ではない場合は定義されない：

TriangularDistributionは，c が min から max までの間にない場合は定義されない：

記号的出力に無効な母数を代入すると意味のない結果が返される：

おもしろい例題  (1)

累積分布関数の等高線を持つ c のさまざまな値についての確率密度関数：

Wolfram Research (2007), TriangularDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/TriangularDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2007), TriangularDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/TriangularDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2007. "TriangularDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/TriangularDistribution.html.

APA

Wolfram Language. (2007). TriangularDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TriangularDistribution.html

BibTeX

@misc{reference.wolfram_2024_triangulardistribution, author="Wolfram Research", title="{TriangularDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/TriangularDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_triangulardistribution, organization={Wolfram Research}, title={TriangularDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/TriangularDistribution.html}, note=[Accessed: 21-November-2024 ]}