VoigtDistribution[δ,σ]
represents Voigt distribution with parameters δ and σ.


VoigtDistribution
VoigtDistribution[δ,σ]
represents Voigt distribution with parameters δ and σ.
Details
- The probability density for value
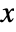 in a Voigt distribution is proportional to
in a Voigt distribution is proportional to 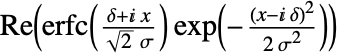 .
. - VoigtDistribution allows δ and σ to be any positive real numbers.
- VoigtDistribution allows δ and σ to be any quantities of the same unit dimensions. »
- VoigtDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- VoigtDistribution[δ,σ] represents a continuous statistical distribution defined and supported over the set of real numbers and parametrized by positive real numbers δ and σ, which together determine the overall behavior of its probability density function (PDF). In general, the PDF of a Voigt distribution is unimodal with a single "peak" (i.e. a global maximum), though its overall shape (its height, its spread, and the horizontal location of its maximum) is determined by the values of δ and σ. In addition, the tails of the PDF are "thin", in the sense that the PDF decreases exponentially rather than decreasing algebraically for large values of
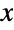 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The Voigt distribution is sometimes referred to as the Voigt profile.
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The Voigt distribution is sometimes referred to as the Voigt profile. - The Voigt distribution is named after German physicist Woldemar Voigt and arose in the modeling of line broadening in spectroscopy and diffraction. In particular, the Voigt distribution is a highly specialized distribution, with many of its modern applications stemming from phenomena in atmospheric sciences and telecommunications related to molecular spectroscopy and radiative transfer.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Voigt distribution. Distributed[x,VoigtDistribution[δ,σ]], written more concisely as xVoigtDistribution[δ,σ], can be used to assert that a random variable x is distributed according to a Voigt distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for Voigt distributions may be given using PDF[VoigtDistribution[δ,σ],x] and CDF[VoigtDistribution[δ,σ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a Voigt distribution, EstimatedDistribution to estimate a Voigt parametric distribution from given data, and FindDistributionParameters to fit data to a Voigt distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Voigt distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Voigt distribution.
- TransformedDistribution can be used to represent a transformed Voigt distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Voigt distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Voigt distributions.
- VoigtDistribution is related to a number of other distributions. VoigtDistribution limits to both NormalDistribution and CauchyDistribution, in the sense that the PDF of VoigtDistribution[δ,σ] tends to that of NormalDistribution[0,σ] and CauchyDistribution[0,δ], respectively, as δ→0 and as σ→0, respectively. Moreover, VoigtDistribution can be realized as a parameter mixture (ParameterMixtureDistribution) of CauchyDistribution and NormalDistribution, in that VoigtDistribution[δ,σ] is precisely CauchyDistribution[μ,δ] when μNormalDistribution[0,σ], and also as a transformation (TransformedDistribution) of NormalDistribution and CauchyDistribution. VoigtDistribution is also closely related to StableDistribution.
Examples
open all close allBasic Examples (3)
Scope (6)
Generate a sample of pseudorandom numbers from a Voigt distribution:
Compare the histogram to the PDF:
Distribution parameter estimation:
Estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
Higher‐order moments of Voigt distribution are indeterminate:
Characteristic function is not differentiable at the origin:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (1)
Properties & Relations (6)
Voigt distribution is closed under addition:
Proof based on characteristic functions:
Relationships to other distributions:
VoigtDistribution[δ,σ] converges to a NormalDistribution as δ->0:
VoigtDistribution[δ,σ] converges to a CauchyDistribution as σ->0:
Parameter mixture of a CauchyDistribution with a centralized NormalDistribution:
The sum of zero mean variables from CauchyDistribution and NormalDistribution:
Related Guides
Text
Wolfram Research (2012), VoigtDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/VoigtDistribution.html (updated 2016).
CMS
Wolfram Language. 2012. "VoigtDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/VoigtDistribution.html.
APA
Wolfram Language. (2012). VoigtDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VoigtDistribution.html
BibTeX
@misc{reference.wolfram_2025_voigtdistribution, author="Wolfram Research", title="{VoigtDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/VoigtDistribution.html}", note=[Accessed: 28-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_voigtdistribution, organization={Wolfram Research}, title={VoigtDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/VoigtDistribution.html}, note=[Accessed: 28-February-2026]}