WakebyDistribution[α,β,γ,δ,μ]
represents Wakeby distribution with shape parameters β and δ, scale parameters α and γ, and location parameter μ.


WakebyDistribution
WakebyDistribution[α,β,γ,δ,μ]
represents Wakeby distribution with shape parameters β and δ, scale parameters α and γ, and location parameter μ.
Details
- The quantile function for value
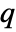 in a Wakeby distribution is equal to
in a Wakeby distribution is equal to 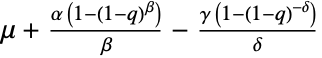 .
. - WakebyDistribution allows α, β, γ, and δ to be any positive real numbers and μ to be any real number.
- WakebyDistribution allows μ, α, and γ to be any quantities of the same unit dimensions, and β and δ to be dimensionless quantities. »
- WakebyDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- WakebyDistribution[α,β,γ,δ,μ] represents a continuous statistical distribution supported on the interval
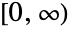 and parametrized by a real number μ (called a "location parameter") and by positive real numbers α, γ, β, and δ (two "scale parameters" and two "shape parameters", respectively), which together determine the overall behavior of its probability density function (PDF). Depending on the values of α, β, γ, δ, and μ, the PDF of a Wakeby distribution may have any of a number of shapes, including unimodal with a single "peak" (i.e. a global maximum), monotone decreasing, and monotone increasing. In addition, the tails of the PDF may be "fat" (i.e. the PDF decreases non-exponentially for large values
and parametrized by a real number μ (called a "location parameter") and by positive real numbers α, γ, β, and δ (two "scale parameters" and two "shape parameters", respectively), which together determine the overall behavior of its probability density function (PDF). Depending on the values of α, β, γ, δ, and μ, the PDF of a Wakeby distribution may have any of a number of shapes, including unimodal with a single "peak" (i.e. a global maximum), monotone decreasing, and monotone increasing. In addition, the tails of the PDF may be "fat" (i.e. the PDF decreases non-exponentially for large values 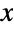 ) or "thin" (i.e. the PDF decreases exponentially for large
) or "thin" (i.e. the PDF decreases exponentially for large 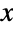 ), depending on the values of α, β, γ, δ, and μ. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.)
), depending on the values of α, β, γ, δ, and μ. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) - The Wakeby distribution was defined by John C. Houghton in the 1970s as an alternative to the LogNormalDistribution and the TukeyLambdaDistribution for modeling flood flows. Its name is derived from Wakeby Pond on Cape Cod, Massachusetts. The Wakeby distribution is described in terms of its quantile function Quantile function or via an inverse distribution function. The Wakeby distribution is highly specialized, and most of its modern applications lie in modeling water-related phenomena in meteorology, hydrology, and precipitation analysis.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Wakeby distribution. Distributed[x,WakebyDistribution[α,β,γ,δ,μ]], written more concisely as xWakebyDistribution[α,β,γ,δ,μ], can be used to assert that a random variable x is distributed according to a Wakeby distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for Wakeby distributions may be given using PDF[WakebyDistribution[α,β,γ,δ,μ],x] and CDF[WakebyDistribution[α,β,γ,δ,μ],x], though neither of these has a known simple closed form. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a Wakeby distribution, EstimatedDistribution to estimate a Wakeby parametric distribution from given data, and FindDistributionParameters to fit data to a Wakeby distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Wakeby distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Wakeby distribution.
- TransformedDistribution can be used to represent a transformed Wakeby distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Wakeby distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Wakeby distributions.
- WakebyDistribution is related to a number of other distributions. Its derivation and application is similar to that of TukeyLambdaDistribution, and in computation one often applies WakebyDistribution as a transformation on the percentiles of BetaDistribution. WakebyDistribution is also related to LogNormalDistribution and hence to NormalDistribution, HalfNormalDistribution, and BinormalDistribution.
Examples
open all close allBasic Examples (4)
Scope (7)
Generate a sample of pseudorandom numbers from a Wakeby distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Different moments of a Wakeby distribution with closed forms as functions of parameters:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (1)
The logarithm of a normalized volume of streamflows is described by WakebyDistribution:
Plot the distribution density function:
Find the probability that the volume of the flow will exceed 10 reference units:
Find the expected volume in reference units, given that it exceeds 10 reference units:
Properties & Relations (2)
Wakeby distribution is closed under translation and scaling by a positive factor:
Wakeby distribution does not have a simple closed form symbolic expression for the PDF:
For certain exact values of the shape coefficients β and δ, the PDF is found by inverting the defining quantile function:
The value of the probability density function can be evaluated numerically for valid numeric parameters:
Related Guides
Text
Wolfram Research (2010), WakebyDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/WakebyDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "WakebyDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/WakebyDistribution.html.
APA
Wolfram Language. (2010). WakebyDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WakebyDistribution.html
BibTeX
@misc{reference.wolfram_2025_wakebydistribution, author="Wolfram Research", title="{WakebyDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/WakebyDistribution.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_wakebydistribution, organization={Wolfram Research}, title={WakebyDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/WakebyDistribution.html}, note=[Accessed: 09-March-2026]}