Zeta

Zeta[s]

gives the Riemann zeta function TemplateBox[{s}, Zeta].

Zeta[s,a]

gives the generalized Riemann zeta function TemplateBox[{s, a}, Zeta2].

Details and Options

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • For 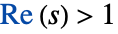Re(s)>1, TemplateBox[{s}, Zeta]=sum_(k=1)^inftyk^(-s).
  • TemplateBox[{s, a}, Zeta2]=sum_(k=0)^(infty)(k+a)^(-s), where any term with 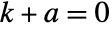is excluded.
  • For 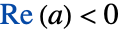Re(a)<0, the definition used is TemplateBox[{s, a}, Zeta2]=sum_(k=0)^(infty)((k+a)^2)^(-s/2).
  • Zeta[s] has no branch cut discontinuities.
  • For certain special arguments, Zeta automatically evaluates to exact values.
  • Zeta can be evaluated to arbitrary numerical precision.
  • Zeta automatically threads over lists.
  • Zeta can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (6)

Evaluate numerically:

Generalized (Hurwitz) zeta function:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Series expansion at the origin:

Series expansion at Infinity:

Series expansion at a singular point:

Scope  (36)

Numerical Evaluation  (7)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate efficiently at high precision:

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

Compute average-case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix Zeta function using MatrixFunction:

Specific Values  (6)

Simple exact values are generated automatically:

Zeta[s,a] for symbolic :

Zeta[s,a] for symbolic :

Value at zero:

Limiting value at infinity:

Find a value of for which Zeta[s]=1.05:

Visualization  (3)

Plot the Zeta function:

Plot the generalized Zeta function for various orders:

Plot the real part of the Zeta function:

Plot the imaginary part of the Zeta function:

Function Properties  (12)

Real domain of Zeta:

Complex domain:

The generalized zeta function TemplateBox[{z, a}, Zeta2] has the same domain for all :

Zeta achieves all real values:

Zeta has the mirror property zeta (TemplateBox[{z}, Conjugate])=TemplateBox[{TemplateBox[{z}, Zeta]}, Conjugate]:

Zeta threads elementwise over lists and matrices:

Zeta is not an analytic function:

However, it is meromorphic:

Zeta is neither non-decreasing nor non-increasing:

However, it is decreasing to the right of the singularity at 1:

Zeta is not injective:

Zeta is surjective:

Zeta is neither non-negative nor non-positive:

TemplateBox[{x, a}, Zeta2] has both singularity and discontinuity at :

TemplateBox[{x}, Zeta] is neither convex nor concave:

However, it is convex to the right of the singularity at :

TraditionalForm formatting:

Differentiation  (3)

First derivative with respect to :

Evaluate derivatives exactly for the Riemann zeta function:

Higher derivatives with respect to :

Plot the higher derivatives with respect to when :

Series Expansions  (2)

Find the Taylor expansion using Series:

Plots of the first three approximations around :

General term in the series expansion using SeriesCoefficient:

Function Identities and Simplifications  (3)

Zeta is defined through the identity:

Sum involving the Zeta function:

Connection with the MoebiusMu function:

Applications  (7)

Plot the real part of the zeta function on the critical line:

Plot the real part across the critical strip:

Find a zero of the zeta function:

Find several zeros:

Use ZetaZero:

Find what fraction of pairs of the first 100 integers are relatively prime:

Compare with a zeta function formula:

Plot real and imaginary parts in the vicinity of two very nearby zeros (a Lehmer pair):

Plot the generalized zeta function:

Use MellinTransform to find the first two terms in the asymptotic expansion for a function that is defined by an infinite series:

Compute the Mellin transform of :

Compute the residues at and to obtain the required asymptotic expansion represented with Zeta function:

Properties & Relations  (8)

Riemann Zeta Function  (5)

The defining sum for the zeta function:

The Euler product formula for the zeta function:

Sum involving a zeta function:

Use FullSimplify to prove the functional equation:

Zeta can be represented as a DifferenceRoot:

Generalized Zeta Function  (3)

The ordinary zeta function is a special case:

In certain cases, FunctionExpand gives formulas in terms of other functions:

Indefinite integral of the generalized zeta function:

Possible Issues  (4)

Real and imaginary parts can have very different scales:

Evaluating the imaginary part accurately requires higher internal precision:

Machine-number inputs can give high‐precision results:

Giving 0 as an argument does not define the precision required:

Including an accuracy specification gives enough information:

In TraditionalForm, ζ is not automatically interpreted as the zeta function:

Neat Examples  (2)

Play the real part of the zeta function on the critical line as a sound:

Animate the zeta function on the critical line:

Wolfram Research (1988), Zeta, Wolfram Language function, https://reference.wolfram.com/language/ref/Zeta.html (updated 2022).

Text

Wolfram Research (1988), Zeta, Wolfram Language function, https://reference.wolfram.com/language/ref/Zeta.html (updated 2022).

CMS

Wolfram Language. 1988. "Zeta." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/Zeta.html.

APA

Wolfram Language. (1988). Zeta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Zeta.html

BibTeX

@misc{reference.wolfram_2024_zeta, author="Wolfram Research", title="{Zeta}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/Zeta.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_zeta, organization={Wolfram Research}, title={Zeta}, year={2022}, url={https://reference.wolfram.com/language/ref/Zeta.html}, note=[Accessed: 18-November-2024 ]}