WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター
微積分

微積分

微分可能な積分と不可能な積分
全微分定積分
未知の関数の導関数領域上の積分
導関数の表し方記号代数的な積分操作
導関数の定義微分方程式
積分法積分変換と関連する演算
不定積分一般化された関数と関連操作
微分
D[f,x]
偏導関数
D[f,x,y,…]
多重偏導関数
D[f,{x,n}]
n 階の偏導関数
D[f,x,NonConstants->{v1,v2,…}]
vi が x に従属するとした上で を求める
偏微分
を求める：
Wolfram Language code: D[x ^ n, x]
三階微分を取る：
Wolfram Language code: D[x ^ n, {x, 3}]
式のどんな項についてでも微分することができる：
Wolfram Language code: D[x[1] ^ 2 + x[2] ^ 2, x[1]]
Dによる微分は偏微分である．この例では，yはxから独立した変数とみなされる
Wolfram Language code: D[x ^ 2 + y ^ 2, x]
yが本当にxに従属するなら，y[x]と記述しxの関数であることを明記する．y'[x]のような項がどう機能するかは「導関数の表し方」を参照のこと
Wolfram Language code: D[x ^ 2 + y[x] ^ 2, x]
Dで微分する際，明示的にxの関数y[x]を与える代りに，yがxに従属していることを指定することも可能である．D[y,x,NonConstants->{y}]は，yがxに従属するときの を表す：
Wolfram Language code: D[x ^ 2 + y ^ 2, x, NonConstants -> {y}]
D[f,{{x1,x2,…}}]
スカラー関数の勾配
D[f,{{x1,x2,…},2}]
f のヘッセ行列
D[f,{{x1,x2,…},n}]
級数 n のテイラー級数係数
D[{f1,f2,…},{{x1,x2,…}}]
ベクトル関数 f のヤコビ多項式
ベクトル微分
の勾配が与えられる：
Wolfram Language code: D[x ^ 2 + y ^ 2, {{x, y}}]
ヘッセ行列が与えられる：
Wolfram Language code: D[x ^ 2 + y ^ 2, {{x, y}, 2}]
ベクトル関数のヤコビ行列が与えられる：
Wolfram Language code: D[{x ^ 2 + y ^ 2, x y}, {{x, y}}]
全微分
Dt[f]
全微分 df
Dt[f,x]
全微分
Dt[f,x,y,…]
多重の全微分 … f
Dt[f,x,Constants->{c1,c2,…}]
ci を定数とする全微分（例 ： dci=0）
y/:Dt[y,x]=0
集合 =0
SetAttributes[c,Constant]
どんな場合でも c を定数とする
全微分
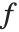ある式 を 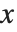について微分するということは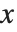， の変化に応じた 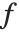の変化の速さを求めることに相当する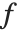． は 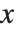に限らず他の変数，例えば 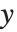や 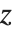等に従属することもある．そのときの導関数がどうなるかは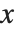， が変化するにつれて 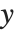と 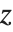がどう変化するかにもよる．
2つの場合が考えられる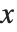． の変化について 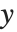と 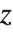が固定されている場合と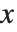， とともに変化する場合である．標準的な偏微分 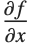では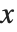， 以外の変数は固定されているとみなされる．一方，全微分 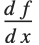では，すべての変数は 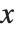の従属変数であるときも許される．
D[f,x] は偏微分を表し，すべての変数は x から独立しているものとされる．また，Dt[f,x] とすると，他の変数は x に依存しているとし全微分が計算される．ともに依存性に関する情報を引数の形で追加できるようになっている．
偏微分 を求める．y は x から独立しているものとする：
Wolfram Language code: D[x ^ 2 + y ^ 2, x]
今度は，y が x に従属しているとした上で，全微分 を求める：
Wolfram Language code: Dt[x ^ 2 + y ^ 2, x]
を置き換えることも可能である：
Wolfram Language code: % /. Dt[y, x] -> yp
また， に明示的な関係を定義付けすることも可能である．その際は，y/:を使って定義する関係が y についてあるものだということを明確にしておく必要がある：
Wolfram Language code: y/:Dt[y, x] = 0
上の定義の後では，Dtは，y が独立変数として扱う：
Wolfram Language code: Dt[x ^ 2 + y ^ 2 + z ^ 2, x]
先の y の導関数に関する関係定義を消去しておく：
Wolfram Language code: Clear[y]
z を固定し全微分を求める：
Wolfram Language code: Dt[x ^ 2 + y ^ 2 + z ^ 2, x, Constants -> {z}]
c を定数と指定する：
Wolfram Language code: SetAttributes[c, Constant]
全微分を再び取る．変数 c が確かに定数として扱われる：
Wolfram Language code: Dt[a ^ 2 + c x ^ 2, x]
c が関数であっても定数とみなされる：
Wolfram Language code: Dt[a ^ 2 + c[x] x ^ 2, x]
全微分 を求める：
Wolfram Language code: Dt[x ^ 2 + c y ^ 2]
全微分に対して置き換えや代入を行うことも可能である：
Wolfram Language code: % /. Dt[y] -> dy
未知の関数の導関数
既知の関数を微分すると明示的な導関数が求まる：
Wolfram Language code: D[Log[x] ^ 2, x]
一方，微分する関数fが未知のとき導関数はf'として求まる：
Wolfram Language code: D[f[x] ^ 2, x]
合成関数の微分ができ，結果の式にf'が残される：
Wolfram Language code: D[x f[x ^ 2], x]
再度，微分する．今度は，f，f'およびf''で導関数が構成される：
Wolfram Language code: D[%, x]
複数の変数を持った関数を微分すると，各変数が何回微分されたかを示す回数が上付き文字の形で導関数の記述に入る：
Wolfram Language code: D[g[x ^ 2, y ^ 2], x]
この入力例は，を表している．Wolfram言語では，どの変数で微分するかの順番は問わない：
Wolfram Language code: D[g[x, y], x, x, y]
xに0を代入し，のときの導関数の値を調べる：
Wolfram Language code: % /. x -> 0
f '[x]
単一の変数からなる関数の一階導関数
f(n)[x]
単一の変数からなる関数の n 階導関数
f(n1,n2,… )[x]
複数の変数からなる関数の導関数（i 番目の変数について ni 階の微分を取る）
未知の関数の導関数の出力形態
導関数の表し方
Wolframシステムの導関数は標準的な数学に現れる導関数と同じように使える．ただし，通常の数学表記は細かい点が省略されており，Wolframシステムにおける導関数の表し方を理解するには，細かい点も含めて考察する必要がある．
数学表記で導関数を と書くとき，正式には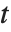， を「ダミー変数」とした 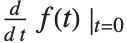を意味する．同様に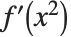，と書けば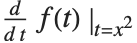，を意味する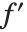． の記述が示唆するように，オブジェクト 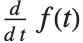は「純粋な関数」とみなせ，その値はパラメータ 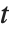の値が決まると計算することができる．ある関数 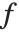を微分するということを，通常 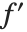と呼ばれる新たな関数を与える演算ととらえてもよい．
関数が複数の引数を持つときは，ダッシュ()を使った簡単な記述ができない．無理に，例えば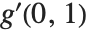，と記述しても，それが 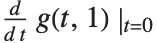を表しているのか，または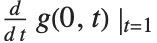，なのか分からずじまいになってしまう．また，これらのオブジェクトは 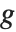として実際に使う関数により値が違ってくるだろう．繰り返すようだが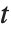， とはダミー変数であり，それを使う理由は単に「どの位置」の変数に対して 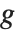を微分するかを指定することにある．
特殊な数学の分野でそうであるように，Wolframシステムでも式ではなく関数に作用するとした微分操作を想定すると便利である．必要な操作内容は，関数 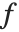を抽出し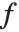， の導関数 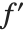を返すというものである．このように変数ではなく関数を操作することを数学用語で演算子と呼ぶ．
つまり，Wolframシステムで得られるオブジェクトf'とは，微分演算子を関数fに適用した結果を示している．f'を完全形で見ると，Derivative[1][f]となっている．Derivative[1]の部分が微分演算子に相当する．
演算子Derivative[n1,n2,…]に与える引数は，引数と同じ「位置」の変数に対して何階の微分を行うか指定する．演算子を使い微分を表しているので，Wolframシステムでは特別な「ダミー変数」を導入する必要はない．
fの導関数を完全形で見てみる：
Wolfram Language code: f'//FullForm
引数としてxを与える：
Wolfram Language code: f'[x]//FullForm
二次の導関数を求める：
Wolfram Language code: f''[x]//FullForm
関数gを第2「位置」に関し微分する：
Wolfram Language code: D[g[x, y], y]
完全形で確認する：
Wolfram Language code: %//FullForm
関数gの第2位置にある変数yに関し二階の導関数を求める：
Wolfram Language code: D[g[x, y], {y, 2}]//FullForm
これは，いろいろな微分成分が入った導関数である：
Wolfram Language code: D[g[x, y], x, y, y]//FullForm
Derivativeでは，各位置に対して何階の微分をするかだけを指定するため，微分の順序は関係ない：
Wolfram Language code: D[g[x, y], y, y, x]//FullForm
もっと複雑な例を見てみよう．gが2つ引数を持ち，両方とも微分変数に依存している：
Wolfram Language code: D[g[x, x], x]
完全形で確認する：
Wolfram Language code: %//FullForm
f'は，基本的に他のWolframシステムの関数と同様に機能する．この関数は引数が何であっても評価可能だし，Wolframシステムの置換記号/.を使い引数を変えることも可能である．（ただし，微分の過程でダミー変数が特別に導入されるとこの操作は使えなくなる．）
原点において評価した関数fの導関数が内部でどう表されるか見てみる：
Wolfram Language code: f'[0]//FullForm
導関数には引数x^2で微分したf'が入る：
Wolfram Language code: D[f[x ^ 2], x]
得られた導関数に置換操作を行うことで の点における導関数の値を求める：
Wolfram Language code: % /. x -> 2
f[x_]のような関数の定義をもとにf'の値を決定するには，多少面倒な処理が必要になる．
関数hを定義する：
Wolfram Language code: h[x_] := x ^ 4
h[x]の導関数を求めると，まず，h[x]が評価され，次に，評価の結果得られる式が微分される：
Wolfram Language code: D[h[x], x]
関数h'を引数xに適用することでも同じ結果が得られる：
Wolfram Language code: h'[x]
関数h'そのものだとどうなるか見てみる：
Wolfram Language code: h'
導関数f'は，関数fの持つ構造により完全に決定される．f[x_]のような関数の定義は，そのままではf'[x]のような式に適用できない．これは，完全形ではf'[x]がDerivative[1][f][x]と表されるためにf[x_]のパターンにマッチできないからである．それでも，多くの場合，f'を単独の関数として扱い，引数を付けないでおいた方が便利である．
Wolframシステムで関数の微分をすると，f'を表す純関数の明示的な定義を検索しようと試みる．例えば，Derivative[1][f]の式を与えると，これがD[f[#],#]&という明示的な形にまず変換され，続いて，可能であれば導関数が評価される．明示的な形ができれば，直ちにf[x_]のような関数定義が使われ導関数が構成される．この微分操作がうまくいけば，関数定義をもとにした導関数が返ってくる．一方，微分演算がうまくいかないと，もとのf'のままで返される．
Tanの導関数が純粋な関数の形で返ってくる：
Wolfram Language code: Tan'
引数yに先の純粋な関数を適用してみる：
Wolfram Language code: %[y]
導関数の定義
引数を1つ持った関数fがあるとき，その導関数はf'[x_]=fp[x]というような割当てをすることで定義できる．
の導関数を と定義する．この例の場合では，:= の代りに = を使っても構わない：
Wolfram Language code: f'[x_] := fp[x]
この導関数を求めると，先に与えたf'[x_]の規則が適用される：
Wolfram Language code: D[f[x ^ 2], x]
再度微分すると の導関数が求まる：
Wolfram Language code: D[%, x]
原点における の導関数が取る値を定義する：
Wolfram Language code: g'[0] = g0
g'[0]の値が使われる：
Wolfram Language code: D[g[x] ^ 2, x] /. x -> 0
gの二次導関数を定義する．引数は何でもよいものとする：
Wolfram Language code: g''[x_] = gpp[x]
二次の導関数に割り当てた関数が使われる：
Wolfram Language code: D[g[x] ^ 2, {x, 2}]
複数の引数からなる関数の導関数を定義するには，Wolfram言語における導関数の一般表記に従って行わなければならない．
f'[x_]:=rhs
f の一階導関数を定義する
Derivative[n][f][x_]:=rhs
f の n 階導関数を定義する
Derivative[m,n,…][g][x_,_,…]:=rhs
複数の引数について g の導関数を定義する
導関数の定義の仕方
2番目の引数についてgの二次導関数を定義する：
Wolfram Language code: Derivative[0, 2][g][x_, y_] := g2p[x, y]
先の定義関係が使われ導関数が求まる：
Wolfram Language code: D[g[a ^ 2, x ^ 2], x, x]
積分法
これは，Wolfram言語における の積分である：
Wolfram Language code: Integrate[x ^ n, x]
やや複雑な例を示す：
Wolfram Language code: Integrate[1 / (x ^ 4 - a ^ 4), x]
Wolfram言語は，標準的な数学関数であればほとんどどんな積分でもできる．ただし，被積分関数は簡単な関数しか含まないときでも，その積分は複雑な関数を取る場合がよくある．標準的な数学関数では全く表現できないことも少なくない．
この積分は明快な方である：
Wolfram Language code: Integrate[Log[1 - x ^ 2], x]
この積分は多重対数関数を使わないと表せない：
Wolfram Language code: Integrate[Log[1 - x ^ 2] / x, x]
Erf関数を含んだ積分の例：
Wolfram Language code: Integrate[Exp[1 - x ^ 2], x]
フレネル(Fresnel)関数を含んだ積分の例：
Wolfram Language code: Integrate[Sin[x ^ 2], x]
こんな積分でも，超幾何関数が必要になる：
Wolfram Language code: Integrate[(1 - x ^ 2) ^ n, x]
この積分は標準的な数学関数では実行できないので入力したままの式が返される：
Wolfram Language code: Integrate[x ^ x, x]
Integrate[f,x]
不定積分 ∫f dx
Integrate[f,x,y]
多重積分 ∫dx dy f
Integrate[f,{x,xmin,xmax}]
定積分 f dx
Integrate[f,{x,xmin,xmax},{y,ymin,ymax}]
多重積分 dxdy f
積分
定積分 を計算する：
Wolfram Language code: Integrate[Sin[x] ^ 2, {x, a, b}]
別の定積分を計算する：
Wolfram Language code: Integrate[Exp[-x ^ 2], {x, 0, Infinity}]
この定積分は式で表現できない：
Wolfram Language code: Integrate[x ^ x, {x, 0, 1}]
しかし，数値的な結果は得ることができる：
Wolfram Language code: N[%]
多重積分 を評価する．最も外側の積分変数に対する区間を最初に指定する：
Wolfram Language code: Integrate[x ^ 2 + y ^ 2, {x, 0, 1}, {y, 0, x}]
これは円領域で を積分する：
Wolfram Language code: Integrate[x ^ 10 Boole[x ^ 2 + y ^ 2 <= 1], {x, -1, 1}, {y, -1, 1}]
不定積分
関数Integrate[f,x]は，不定積分 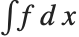を返す．不定積分は微分の逆操作ととらえてもよいだろう．Integrate[f,x]で積分した結果を微分すると，必ずもとの式 f と数学的に等しい結果が得られる．
一般に，微分を取ると f になる関数はいくつも存在する．Integrate[f,x]はその内の1つにすぎない．微分した形が同じになる関数は任意の積分定数を加えたり，離散点以外では定数である任意の関数を加えることで他にいくらでも構成できる．
特別に積分範囲を指定した定積分では，積分定数は消えてしまう．不定積分は任意定数分の不確定さはあるものの，積分範囲を指定しないままの方が都合がよいことも多い．
標準的な規則が適用され不定積分が求められる：
Wolfram Language code: Integrate[x ^ 2, x]
任意な定数を不定積分に加えても，微分すれば同じ形が得られる．Integrateは同じ導関数を持った関数の1つでしかない：
Wolfram Language code: D[% + c, x]
不定積分 を求める：
Wolfram Language code: Integrate[1 / (x ^ 2 - 1), x]
微分することでもとの関数が得られるはずである：
Wolfram Language code: D[%, x]
手を加えなければもとの式が得られない：
Wolfram Language code: Simplify[%]
関数Integrateの機能の仕方として，積分変数に従属していることが明示的に示されていない関数または変数は，積分変数から独立しているとみなされ定数として扱われる．このため，Integrateは偏微分関数Dの逆関数のように機能する．
変数aはxから独立しているとみなされる：
Wolfram Language code: Integrate[a x ^ 2, x]
数学の演算操作を必要としない式であればどんな式でも積分変数として指定してよい：
Wolfram Language code: Integrate[x b[x] ^ 2, b[x]]
Integrateでは，さらに，積分式にある未知な項はすべて「一般的」な値を持つものとして扱われる．例えば，積分 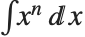を求めると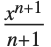，が求まる．これは，一般的な n の値では正解でよいが，の特殊な場合には間違いになってしまう．
nは-1ではないとされ，標準的な積分が行われる：
Wolfram Language code: Integrate[x ^ n, x]
指数に-1を指定すると，先とは異なる結果を返してくる：
Wolfram Language code: Integrate[x ^ -1, x]
ある積分をしたなら，結果として得られる式はいくつもの形で書き表すことが可能である．Wolfram言語はその中でも最も使いやすい形を見付けて返すようになっている．例えば，複素数で入力をしていなければ積分における複素数の明示的な提示はしない．
ArcTanが使われ積分が構成される：
Wolfram Language code: Integrate[1 / (1 + a x ^ 2), x]
今度は，積分にArcTanhが使われる：
Wolfram Language code: Integrate[1 / (1 - b x ^ 2), x]
これは数学的に最初の積分に等しい．しかし，構成される形は微妙に違っている：
Wolfram Language code: % /. b -> -a
それでも，導関数は正確である：
Wolfram Language code: D[%, x]
見た目には違うように映るが，ArcTan[x]と-ArcTan[1/x]はともにの不定積分として求まる：
Wolfram Language code: Simplify[D[{ArcTan[x], -ArcTan[1 / x]}, x]]
Integrateは，最終的により単純な形にする：
Wolfram Language code: Integrate[1 / (1 + x ^ 2), x]
可能な積分と不可能な積分
積分は微分よりずっと難しい．微分には合成関数の微分法等の手法があるので，どんな微分でも体系だった手順に従って求めることができる．積分には，そのような手順がない．
積分における主な問題は，対象とする関数の原始関数を見付けるのが難しいことにある．微分をしたなら，必ず，微分する前の関数と同程度か，または，それより簡単な関数が取得できる．積分の場合はそうはいかず，通常は，もとの関数よりずっと難解な関数が必要になってしまう．
この例の積分では，入力したもとの関数が使われる：
Wolfram Language code: Integrate[Log[x] ^ 2, x]
この例の積分を求めるには，特殊関数LogIntegralが必要になる：
Wolfram Language code: Integrate[Log[Log[x]], x]
各種の関数で表される積分を見付けるのは難しくない：
Wolfram Language code: Integrate[Sin[x ^ 2], x]
この積分には不完全ガンマ関数が必要になる．答において，x がどんな複素数の値を取ろうが問題ないように解が構成されることに注目：
Wolfram Language code: Integrate[Exp[-x ^ a], x]
Wolfram言語には数学で使う各種の関数が多数組み込まれている．これらの関数を使うことで，非常に多くの積分を求めることができる．それでも，一見簡単に見えるが実は難解で標準的な数学の関数では求まらない積分がいくつもある．
この積分は一見簡単に見えるが，実は難解で，標準的な数学の関数では求まらない：
Wolfram Language code: Integrate[Sin[x] / Log[x], x]
標準的な数学関数を使って原始関数を表したい主な理由は，積分で得られる結果を評価したりさらに変形操作を施したりする上でそれらの関数の持つ既知の性質が使えるからである．
通常使われる関数の場合，指数関数や対数関数もしくは三角関数等の初等関数だけを使って積分が求まる．Integrateの重要な機能のひとつに，ある関数の積分がこのような初等関数だけで表されるとき，Integrateはその関数の積分を必ず見付けることができるというものがある．
有理関数の積分なら問題なく計算できる．求まる積分は有理関数と対数関数，そして逆三角関数で構成される：
Wolfram Language code: Integrate[x / ((x - 1)(x + 2)), x]
この積分も同じ形を持つが，多項式の根について取った陰な和が入るところが違う：
Wolfram Language code: Integrate[1 / (1 + 2 x + x ^ 3), x]
解の式すべてを数値近似する：
Wolfram Language code: N[%]
三角関数の式を積分すると，通常，答の式も三角関数で構成される：
Wolfram Language code: Integrate[Sin[x] ^ 3 Cos[x] ^ 2, x]
代数演算の関数を使った簡単な式を積分してみよう：
Wolfram Language code: Integrate[Sqrt[x] Sqrt[1 + x], x]
今度は，ネストした平方根を積分する：
Wolfram Language code: Integrate[Sqrt[x + Sqrt[x]], x]
初等関数を合成した式の積分は，求まった積分も初等関数で構成されるときがある：
Wolfram Language code: Integrate[Cos[Log[x]], x]
しかし，この例のような別の種類の関数が必要になる式はさらに多くある：
Wolfram Language code: Integrate[Log[Cos[x]], x]
この種の積分は楕円関数を使わないと解けない：
Wolfram Language code: Integrate[Sqrt[Cos[x]], x]
それでも，初等関数だけで積分が解けるときもある：
Wolfram Language code: Integrate[Sqrt[Tan[x]], x]
このような積分はPiecewiseを用いて系統的に行うことができる：
Wolfram Language code: Integrate[2 ^ Max[x, 1 - x], x]
Integrateでは，初等関数以外にも，多数のアルゴリズムが使われ特殊関数の積分が行われる．アルゴリズムのいくつかは初等関数のときの積分法を直接一般化した手法に基づいている．しかし，多くの場合，被積分関数を特殊な関数で表しておいて，その積分を求めた上で，適当に一般的によく知られている関数に帰着させる方法が取られる．
このベッセル関数を積分するには，一般化された超幾何関数が必要になる：
Wolfram Language code: Integrate[BesselJ[0, x], x]
式によっては，積分するとより分かりやすい形になる：
Wolfram Language code: Integrate[x ^ 3 BesselJ[0, x], x]
積分の公式を集めた本にはおよそ数千の不定積分が記載されている．Wolfram言語は基本的にそのすべての積分を計算できる．さらに，Wolfram言語には汎用アルゴリズムが備えられているので，特定の問題だけでなく非常に広範囲に渡る積分問題が解けるようにもなっている．
この積分は大きな積分の公式集なら必ず載っている：
Wolfram Language code: Integrate[Log[1 - x] / x, x]
この積分は公式集を参照しただけでは解けない．もっと一般化されたアルゴリズムが必要になる：
Wolfram Language code: Integrate[Log[1 + 3 x + x ^ 2] / x, x]
特に，ユーザ定義の数学関数を導入したなら，新しい種類の積分法をWolfram言語に教えておくとよいだろう．これはIntegrateに定義を付け加えることでできる．
微分の計算をする場合，合成関数の微分法を使えば，Wolfram言語のDerivativeを使って標準的な形の関数が得られる．しかし，積分の場合は，そのような標準形がないので，場合によっては同じ積分から得られるいくつかの変形版を特別に定義してやらなければいけない．また，Integrateを使っても，自動的な変数の変換や他の変換操作はなかなかうまくできない．
Wolfram言語に用意されている標準的な数学関数ではこの積分はできない：
Wolfram Language code: Integrate[Sin[Sin[x]], x]
積分用の規則を追加する前にプロテクトを解除しておく：
Wolfram Language code: Unprotect[Integrate]
この式の積分を例えば「ジョーンズ」(Jones)関数とするユーザ定義の規則を設ける：
Wolfram Language code: Integrate[Sin[Sin[a_. + b_. x_]], x_] := Jones[a, x] / b
実際に積分してみる．Jones関数が使われ答が構成される：
Wolfram Language code: Integrate[Sin[Sin[3x]], x]
積分 は 超幾何関数の無限和かあるいは適当に一般化された二変数のカンペドフェリエ(Kampé de Fériet)超幾何関数を用いて表される．
積分は微分よりずっと難しい．微分には合成関数の微分法等の手法があるので，どんな微分でも体系だった手順に従って求めることができる．積分には，そのような手順がない．
積分における主な問題は，対象とする関数の原始関数を見付けるのが難しいことにある．微分をしたなら，必ず，微分する前の関数と同程度か，または，それより簡単な関数が取得できる．積分の場合はそうはいかず，通常は，もとの関数よりずっと難解な関数が必要になってしまう．
この例の積分では，入力したもとの関数が使われる：
Wolfram Language code: Integrate[Log[x] ^ 2, x]
この例の積分を求めるには，特殊関数LogIntegralが必要になる：
Wolfram Language code: Integrate[Log[Log[x]], x]
各種の関数で表される積分を見付けるのは難しくない：
Wolfram Language code: Integrate[Sin[x ^ 2], x]
この積分には不完全ガンマ関数が必要になる．答において，x がどんな複素数の値を取ろうが問題ないように解が構成されることに注目：
Wolfram Language code: Integrate[Exp[-x ^ a], x]
Wolfram言語には数学で使う各種の関数が多数組み込まれている．これらの関数を使うことで，非常に多くの積分を求めることができる．それでも，一見簡単に見えるが実は難解で標準的な数学の関数では求まらない積分がいくつもある．
この積分は一見簡単に見えるが，実は難解で，標準的な数学の関数では求まらない：
Wolfram Language code: Integrate[Sin[x] / Log[x], x]
標準的な数学関数を使って原始関数を表したい主な理由は，積分で得られる結果を評価したりさらに変形操作を施したりする上でそれらの関数の持つ既知の性質が使えるからである．
通常使われる関数の場合，指数関数や対数関数もしくは三角関数等の初等関数だけを使って積分が求まる．Integrateの重要な機能のひとつに，ある関数の積分がこのような初等関数だけで表されるとき，Integrateはその関数の積分を必ず見付けることができるというものがある．
有理関数の積分なら問題なく計算できる．求まる積分は有理関数と対数関数，そして逆三角関数で構成される：
Wolfram Language code: Integrate[x / ((x - 1)(x + 2)), x]
この積分も同じ形を持つが，多項式の根について取った陰な和が入るところが違う：
Wolfram Language code: Integrate[1 / (1 + 2 x + x ^ 3), x]
解の式すべてを数値近似する：
Wolfram Language code: N[%]
三角関数の式を積分すると，通常，答の式も三角関数で構成される：
Wolfram Language code: Integrate[Sin[x] ^ 3 Cos[x] ^ 2, x]
代数演算の関数を使った簡単な式を積分してみよう：
Wolfram Language code: Integrate[Sqrt[x] Sqrt[1 + x], x]
今度は，ネストした平方根を積分する：
Wolfram Language code: Integrate[Sqrt[x + Sqrt[x]], x]
初等関数を合成した式の積分は，求まった積分も初等関数で構成されるときがある：
Wolfram Language code: Integrate[Cos[Log[x]], x]
しかし，この例のような別の種類の関数が必要になる式はさらに多くある：
Wolfram Language code: Integrate[Log[Cos[x]], x]
この種の積分は楕円関数を使わないと解けない：
Wolfram Language code: Integrate[Sqrt[Cos[x]], x]
それでも，初等関数だけで積分が解けるときもある：
Wolfram Language code: Integrate[Sqrt[Tan[x]], x]
このような積分はPiecewiseを用いて系統的に行うことができる：
Wolfram Language code: Integrate[2 ^ Max[x, 1 - x], x]
Integrateでは，初等関数以外にも，多数のアルゴリズムが使われ特殊関数の積分が行われる．アルゴリズムのいくつかは初等関数のときの積分法を直接一般化した手法に基づいている．しかし，多くの場合，被積分関数を特殊な関数で表しておいて，その積分を求めた上で，適当に一般的によく知られている関数に帰着させる方法が取られる．
このベッセル関数を積分するには，一般化された超幾何関数が必要になる：
Wolfram Language code: Integrate[BesselJ[0, x], x]
式によっては，積分するとより分かりやすい形になる：
Wolfram Language code: Integrate[x ^ 3 BesselJ[0, x], x]
積分の公式を集めた本にはおよそ数千の不定積分が記載されている．Wolfram言語は基本的にそのすべての積分を計算できる．さらに，Wolfram言語には汎用アルゴリズムが備えられているので，特定の問題だけでなく非常に広範囲に渡る積分問題が解けるようにもなっている．
この積分は大きな積分の公式集なら必ず載っている：
Wolfram Language code: Integrate[Log[1 - x] / x, x]
この積分は公式集を参照しただけでは解けない．もっと一般化されたアルゴリズムが必要になる：
Wolfram Language code: Integrate[Log[1 + 3 x + x ^ 2] / x, x]
特に，ユーザ定義の数学関数を導入したなら，新しい種類の積分法をWolfram言語に教えておくとよいだろう．これはIntegrateに定義を付け加えることでできる．
微分の計算をする場合，合成関数の微分法を使えば，Wolfram言語のDerivativeを使って標準的な形の関数が得られる．しかし，積分の場合は，そのような標準形がないので，場合によっては同じ積分から得られるいくつかの変形版を特別に定義してやらなければいけない．また，Integrateを使っても，自動的な変数の変換や他の変換操作はなかなかうまくできない．
Wolfram言語に用意されている標準的な数学関数ではこの積分はできない：
Wolfram Language code: Integrate[Sin[Sin[x]], x]
積分用の規則を追加する前にプロテクトを解除しておく：
Wolfram Language code: Unprotect[Integrate]
この式の積分を例えば「ジョーンズ」(Jones)関数とするユーザ定義の規則を設ける：
Wolfram Language code: Integrate[Sin[Sin[a_. + b_. x_]], x_] := Jones[a, x] / b
実際に積分してみる．Jones関数が使われ答が構成される：
Wolfram Language code: Integrate[Sin[Sin[3x]], x]
積分 は 超幾何関数の無限和かあるいは適当に一般化された二変数のカンペドフェリエ(Kampé de Fériet)超幾何関数を用いて表される．
定積分
Integrate[f,x]
不定積分
Integrate[f,{x,xmin,xmax}]
定積分
Integrate[f,{x,xmin,xmax},{y,ymin,ymax}]
多重積分
積分関数
を積分する：
Wolfram Language code: Integrate[x ^ 2, {x, a, b}]
多重積分 を求める：
Wolfram Language code: Integrate[x ^ 2 + y ^ 2, {x, 0, a}, {y, 0, b}]
この多重積分では，最初にyに関して積分が行われる．また，積分範囲はxに依存している．積分順序はSumやTableで使われる順序と同じである：
Wolfram Language code: Integrate[x ^ 2 + y ^ 2, {x, 0, a}, {y, 0, x}]
簡単な定積分なら，まず不定積分を探し，見付かった不定形を必要な積分範囲で計算することで定積分が求まる．大多数の不定積分は標準的な数学関数で表せない．定積分なら，難解なものでも解けるものがある．
この不定積分は標準的な数学関数では求まらない：
Wolfram Language code: Integrate[Cos[Sin[x]], x]
同じ積分式の定積分はベッセル関数を使って解ける：
Wolfram Language code: Integrate[Cos[Sin[x]], {x, 0, 2Pi}]
不定形でもこの積分を求めることは可能だが，定積分の方が素直に求まる：
Wolfram Language code: Integrate[Log[x] Exp[-x ^ 2], {x, 0, Infinity}]
積分式に特殊関数があるからといって，その定積分が難解になるとは限らない：
Wolfram Language code: Integrate[BesselK[0, x] ^ 2, {x, 0, Infinity}]
それでも，この積分には特殊関数が必要になる：
Wolfram Language code: Integrate[BesselK[0, x] BesselJ[0, x], {x, 0, Infinity}]
この被積分関数は簡単なものだが，その定積分はそうでない：
Wolfram Language code: Integrate[Sin[x ^ 2] Exp[-x], {x, 0, Infinity}]
不定積分が見付かったとしても，単に見付かった不定積分の上限と下限における値の差を取っただけでは定積分の値は求まらないことが多い．積分の領域によっては特異点が存在することがあり，この手順ではそのような特徴を見逃すことがあるからである．
の不定積分を計算する：
Wolfram Language code: Integrate[1 / x ^ 2, x]
上限と下限における不定形の値を差し引く：
Wolfram Language code: Limit[%, x -> 2] - Limit[%, x -> -2]
の点に二重の極が存在するため真の定積分は発散してしまう：
Wolfram Language code: Integrate[1 / x ^ 2, {x, -2, 2}]
この例は微妙な問題を含んでいる．極はないが分岐がある：
Wolfram Language code: Integrate[1 / (1 + a Sin[x]), x]
不定積分の式を使い範囲両端の差を取ると0になってしまう：
Wolfram Language code: Limit[%, x -> 2Pi] - Limit[%, x -> 0]
正式な定積分を計算する．答は に従属する．前提条件で収束が約束される：
Wolfram Language code: Integrate[1 / (1 + a Sin[x]), {x, 0, 2Pi}, Assumptions -> -1 < a < 1]
Integrate[f,{x,xmin,xmax},PrincipalValue->True]
定積分のコーシー主値を求める
主値定積分
の不定積分を求める：
Wolfram Language code: Integrate[1 / x, x]
とにおける極限を計算し，それらの差を取る． を含んだおかしな結果が得られてしまう：
Wolfram Language code: Limit[%, x -> 2] - Limit[%, x -> -1]
この通常のリーマン定積分は発散してしまう：
Wolfram Language code: Integrate[1 / x, {x, -1, 2}]
それでもコーシー主値は有限値になる：
Wolfram Language code: Integrate[1 / x, {x, -1, 2}, PrincipalValue -> True]
不定積分がパラメータを含むとき，パラメータの取り得るほとんどすべての値に対して正しい結果となる式を求めることができる．しかし，定積分となるとその限りではない．定積分で見られる最もよくある問題は，パラメータが特別な条件を満たす場合に限って定積分が収束することがある，というものである．
求まる不定積分はすべての の条件に対して有効である：
Wolfram Language code: Integrate[x ^ n, x]
この定積分が収束するには， はある条件を満足しなければいけない：
Wolfram Language code: Integrate[x ^ n, {x, 0, 1}]
に2を代入すると，条件は満たされる：
Wolfram Language code: % /. n -> 2
オプション
デフォルト値
GenerateConditionsAutomatic
条件式を生成するかしないかを指定する
Assumptions$Assumptions
パラメータに関する仮定を指定する
Integrateのオプション
を前提としたとき答は常にになる：
Wolfram Language code: Integrate[x ^ n, {x, 0, 1}, Assumptions -> (n > 2)]
定積分が収束するときでも，積分路に特異点があればパラメータが変化すると不連続な変化が生じる．場合によっては，Signのような関数を組み込むことで不連続性を考慮した答を単一式にまとめることは可能だが，Ifを使った方がまとめやすい場合もある．
積分の収束条件がIfで与えられる：
Wolfram Language code: Integrate[Sin[a x] / x, {x, 0, Infinity}]
得られる結果は が実数であるという前提から求まる：
Wolfram Language code: Integrate[Sin[a x] / x, {x, 0, Infinity}, Assumptions -> Im[a] == 0]
グラフから，の関数として不連続なことが分かる．不連続性は における の持つ特異点に起因している：
Wolfram Language code: Plot[%, {a, -5, 5}]
Signを使った式では答を表しづらいため，Ifが代りに使われる：
Wolfram Language code: Integrate[Sin[x] BesselJ[0, a x] / x, {x, 0, Infinity}, Assumptions -> Im[a] == 0]
求まった の関数をプロットする：
Wolfram Language code: Plot[Evaluate[%], {a, -5, 5}]
領域上の積分
これは単位円の内側の積分を行う：
Wolfram Language code: Integrate[If[x ^ 2 + y ^ 2 < 1, 1, 0], {x, -1, 1}, {y, -1, 1}]
これは相当の形である：
Wolfram Language code: Integrate[Boole[x ^ 2 + y ^ 2 < 1], {x, -1, 1}, {y, -1, 1}]
単純な矩形領域における積分は極めて簡単であるが，円形領域になるとはるかに複雑になる．
これはベッセル関数を与える：
Wolfram Language code: Integrate[Exp[x] Boole[x ^ 2 + y ^ 2 < 1], {x, -1, 1}, {y, -1, 1}]
Integrate[f Boole[cond],{x,xmin,xmax},{y,ymin,ymax}]
cond が Trueになる領域で f を積分する
領域上の積分
特に領域を定義している条件内にパラメータがある場合は，領域上の積分の結果はいくつかの場合に分かれることがある．
これは の区分関数を与える：
Wolfram Language code: Integrate[Boole[a x < y], {x, 0, 1}, {y, 0, 1}]
パラメータが2つだと，これでさえかなりな部分に分割される：
Wolfram Language code: Integrate[Boole[a x < b], {x, 0, 1}]
これは円と正方形の交差を含む：
Wolfram Language code: Integrate[Boole[x ^ 2 + y ^ 2 < a], {x, 0, 1}, {y, 0, 1}]
この領域には無限の要素がある可能性がある：
Wolfram Language code: Integrate[Boole[Sin[x] > 1 / 2] Exp[-x], {x, 0, Infinity}]
記号代数的な積分操作
Wolfram言語が積分できない場合，積分は記号式のままに置いておかれる．この積分記号のままの式は引き続き変形操作等を施すことが可能である．
Wolfram言語では積分できない．積分のまま残される：
Wolfram Language code: Integrate[x ^ 2 f[x], x]
積分記号のままの式を微分するともとの被積分関数が求まる：
Wolfram Language code: D[%, x]
明示的な式では求まらない定積分を見てみる：
Wolfram Language code: Integrate[f[x], {x, a[x], b[x]}]
求めた定積分から導関数を求める：
Wolfram Language code: D[%, x]
この定積分の積分範囲はxに明示的に従属していない：
Wolfram Language code: defint = Integrate[f[x], {x, a, b}]
uについて偏微分を取る．答は0になる：
Wolfram Language code: D[defint, u]
それでも，自明でない全微分が存在する：
Wolfram Language code: Dt[defint, u]
微分方程式
Wolfram言語の関数DSolveを使って常微分方程式および偏微分方程式の解をシンボル的に求めることが可能である．
微分方程式を解くということは，基本的に未知な関数の取る形を見出すことである．Wolfram言語では，未知の関数はy[x]のような式で表される．また，導関数はy'[x]やy''[x]のように表される．
組込み関数DSolveは，関数規則として求まる解をリスト形式で返す．ここで，解が割り当てられる関数がどのように表されているかで，その先の解の応用が左右されることがある．DSolveにy[x]について解くように指定すると，DSolveは確かにy[x]についての規則を返す．問題によっては，この割付規則で十分事が足りる．ただし，そのままでは，y'[x]の値，さらには，y[0]の値さえも生成できない．このため，DSolveでは，y[x]についてではなくy自体について解くように指定した方が都合よくなる．そうすれば，DSolveからはyを純関数として与える規則が求まる．純関数に関しては「純関数」を参照のこと．
DSolveを使いy[x]について解く．y[x]に対する規則が求まる：
Wolfram Language code: DSolve[y'[x] + y[x] == 1, y[x], x]
この規則はy[x]だけに限って適用可能である．y[0]やy'[x]には適用できない：
Wolfram Language code: y[x] + 2y'[x] + y[0] /. %
一方，DSolveを使ってyについて解くと，関数yを純関数とする規則が求まる：
Wolfram Language code: DSolve[y'[x] + y[x] == 1, y, x]
今度の規則は，yが微分の形で現れても適用可能である：
Wolfram Language code: y[x] + 2y'[x] + y[0] /. %
解をもとの方程式に代入するとTrueとなる：
Wolfram Language code: y'[x] + y[x] == 1 /. %%
DSolve[eqn,y[x],x]
微分方程式を y[x] について解く
DSolve[eqn,y,x]
微分方程式を関数 y について解く
微分方程式の解法と2つの解の形
標準的な数学表記法では，微分方程式の解を構成するとき，よく「ダミー変数」を導入し解に現れる関数の引数を表すようにする．解を表すための数式だけが必要なら，ダミー変数を導入することは確かに便利である．しかし，解をその他の計算に適用したい場合には，ダミー変数を使わずに純関数として解を得た方が有利だろう．ただし，純関数はWolfram言語では簡単に表せるが，それに直接相当する数学の標準的な記述は存在しないことに注意されたい．
DSolve[{eqn1,eqn2,…},{y1,y2,…},x]
リスト形式で与えられた連立微分方程式を解く
連立微分方程式の解法
連立している2つの微分方程式を解く：
Wolfram Language code: DSolve[{y[x] == -z'[x], z[x] == -y'[x]}, {y, z}, x]
この式では，yに関して2つの異なる解が求まる：
Wolfram Language code: DSolve[y[x] y'[x] == 1, y, x]
y[0]==0のような式を特別に追加することで，微分方程式に初期条件や境界条件が付加できる．
y[0]==1の条件を満たす解を求める：
Wolfram Language code: DSolve[{y'[x] == a y[x], y[0] == 1}, y[x], x]
制約条件や境界条件なしで連立微分方程式を解くと，Wolfram言語では一般解が求められる．一般解には未定な「積分定数」がいくつか含まれる．各方程式の持つ導関数の階数に応じて1つずつ新たな定数が導入される．
定数にはデフォルトでC[n]というように名前が付けられる．添数 n は開始値が1で，DSolveが使われるたびにリセットされる．これは，オプションGeneratedParametersを特別に設定することでオーバーライドすることができる．関数をオプションに割り当てると，DSolveが使われるたびにそれが n の取る各添数値に適用され各定数の添数が決定される．
四次方程式の一般解を求める．解には未定係数が4つ必要になる：
Wolfram Language code: DSolve[y''''[x] == y[x], y[x], x]
独立した初期条件や境界条件を1つ与えると必要になる未定係数が1つ減る：
Wolfram Language code: DSolve[{y''''[x] == y[x], y[0] == y'[0] == 0}, y[x], x]
微分方程式の解を厳密な数式として求めることは非常に難しい．事実，標準的な数学関数で構成できるような式が存在するのはごく限られた数の方程式しかない．
最もよく研究されてきた微分方程式は，解法の対象になる関数とその導関数が線形な系である線形方程式である．
斉次一次線形方程式を解く．簡単な解が求まる：
Wolfram Language code: DSolve[y'[x] - x y[x] == 0, y[x], x]
非斉次方程式にすると，途端に複雑な解になってしまう：
Wolfram Language code: DSolve[y'[x] - x y[x] == 1, y[x], x]
単一の線形微分方程式を解くとき，解法の対象にする関数の一次導関数だけを方程式が持つとき，積分をするだけで必ず解が求まることが分かっている．
しかし，微分方程式が2つ以上になるか，二次以上の導関数を持つと，その限りではなくなる．それでも，単純な二次の線形微分方程式によっては，「特殊関数」に示した各種特殊関数を使い解くことが可能である．事実，特殊関数の多くはそもそもこの種の方程式を解くために導入された，という歴史的な経緯を持っている．
エアリー(Airy)方程式を解く．解法にはエアリー関数が使われる：
Wolfram Language code: DSolve[y''[x] - x y[x] == 0, y[x], x]
ベッセル(Bessel)関数が使われ解が求まる：
Wolfram Language code: DSolve[y''[x] - Exp[x] y[x] == 0, y[x], x]
マシュー(Mathieu)関数が使われ解が求まる：
Wolfram Language code: DSolve[y''[x] + Cos[x] y[x] == 0, y, x]
ここではルジャンドル(Legendre)関数が使われる：
Wolfram Language code: DSolve[y''[x] - Cot[x] ^ 2 y[x] == 0, y[x], x]
二次の線形方程式の中には，初等関数だけで解けるものもある：
Wolfram Language code: DSolve[x ^ 2 y''[x] + y[x] == 0, y[x], x]
二次より高次の線形微分方程式になると，ごく単純な形を持ったものでも解法に必要な関数は非常に難解になる．三次の場合，方程式によってはマイヤー(Meijer)のG関数MeijerGが使えるときがある．四次以上の高次方程式には，標準的な数学関数はごくまれなケースを除き全く使えない．
三次の線形微分方程式を解く．一般化された超幾何関数が使われ解が求まる：
Wolfram Language code: DSolve[y'''[x] + x y[x] == 0, y[x], x]
この方程式にはさらに一般化されたマイヤーのG関数が必要になる：
Wolfram Language code: DSolve[y'''[x] + Exp[x] y[x] == 0, y[x], x]
非線形な微分方程式だと，限られた特殊ケースにおいてだけ標準的な数学関数を使って解くことが可能である．ただし，DSolveには汎用的な手続きが使われているので，標準公式集に解が載っているような非線形微分方程式であればほとんど解けるようになっている．
一次非線形微分方程式を解いてみる． 自体が式になければ割合簡単に解が求まる：
Wolfram Language code: DSolve[y'[x] - y[x] ^ 2 == 0, y[x], x]
リッカティ(Riccati)方程式になると，解法は非常に複雑なものになってしまう：
Wolfram Language code: DSolve[y'[x] - y[x] ^ 2 == x, y[x], x]//FullSimplify
それでも，このベルヌーイ(Bernoulli)の方程式は割合簡単に解ける：
Wolfram Language code: DSolve[y'[x] - x y[x] ^ 2 - y[x] == 0, y[x], x]
番目のベルヌーイの方程式は，一般に個の明示的な解を持つ：
Wolfram Language code: DSolve[y'[x] - x y[x] ^ 3 + y[x] == 0, y[x], x]
このアーベル(Abel)方程式も解けるが，解は陰的な形でしか求まらない：
Wolfram Language code: DSolve[y'[x] + x y[x] ^ 3 + y[x] ^ 2 == 0, y[x], x]
実際に区分関数を使う微分方程式を用意すると便利である．そのような式に対してはDSolveを使い，記号的な解を得ることができる．
この式は区分関数を含む：
Wolfram Language code: DSolve[y'[x] - y[x] == UnitStep[x], y[x], x]
ここでは解が3個のケースに分かれる：
Wolfram Language code: DSolve[y'[x] + Clip[x] y[x] == 0, y[x], x]
常微分方程式以上の場合は，微分方程式と代数方程式を混合したものを含む「微分代数方程式」と考えることができる．
微分代数方程式を解く：
Wolfram Language code: DSolve[{y'[x] + 3z'[x] == 4 y[x] + 1 / x, y[x] + z[x] == 1}, {y[x], z[x]}, x]
DSolve[eqn,y[x1,x2,…],{x1,x2,…}]
偏微分方程式を y[x1,x2,…]について解く
DSolve[eqn,y,{x1,x2,…}]
偏微分方程式を関数 y について解く
偏微分方程式を解く
DSolveは一変数の常微分方程式だけでなく，2個以上の変数が現れる偏微分方程式も扱えるようになっている．
二変数の簡単な偏微分方程式の解を求める：
Wolfram Language code: DSolve[D[y[x1, x2], x1] + D[y[x1, x2], x2] == 1 / (x1 x2), y[x1, x2], {x1, x2}]
純関数として表された解：
Wolfram Language code: DSolve[D[y[x1, x2], x1] + D[y[x1, x2], x2] == 1 / (x1 x2), y, {x1, x2}]
偏微分方程式の数学理論は常微分のそれと比べてかなり複雑である．そのひとつの理由は，常微分方程式の一般解は単に定数しか含まないのに対し，偏微分方程式の一般解は，見付かったとしても任意関数を含んだ形となることである．実際 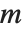変数の偏微分方程式の一般解には 変数の任意関数が含まれる．DSolveはデフォルトでこのような関数をC[n]で表す．
三変数の簡単な偏微分方程式：
Wolfram Language code: (D[#, x1] + D[#, x2] + D[#, x3])&[y[x1, x2, x3]] == 0
解は二変数の任意関数を含む：
Wolfram Language code: DSolve[%, y[x1, x2, x3], {x1, x2, x3}]
一次元波動方程式：
Wolfram Language code: (c ^ 2 D[#, x, x] - D[#, t, t])&[y[x, t]] == 0
この二階方程式の解は2つの任意関数を含む：
Wolfram Language code: DSolve[%, y[x, t], {x, t}]
常微分方程式には解の存在が保証されており，初期条件あるいは境界条件を与えることは，一般解に含まれる積分定数の値を決定することに過ぎない．しかし偏微分方程式に関してはそうではない．実際，線形偏微分方程式かその他のまれな特別の型の偏微分方程式しかそのような一般解を持たない．
他の偏微分方程式は初期条件あるいは境界条件が与えられたときのみ解くことができる．そしてほとんどの場合，解が標準的な数学関数で表せることはない．
yとその微分が線形に現れるとき，一般解が存在する：
Wolfram Language code: DSolve[x1 D[y[x1, x2], x1] + x2 D[y[x1, x2], x2] == Exp[x1 x2], y[x1, x2], {x1, x2}]
この非線形微分不定式は，一般解を持つ：
Wolfram Language code: DSolve[D[y[x1, x2], x1] + D[y[x1, x2], x2] == Exp[y[x1, x2]], y[x1, x2], {x1, x2}]//Quiet
この偏微分方程式は一般解を持たない：
Wolfram Language code: DSolve[D[y[x1, x2], x1] D[y[x1, x2], x2] == a, y[x1, x2], {x1, x2}]
積分変換と関連する演算

ラプラス変換

LaplaceTransform[expr,t,s]
式 expr のラプラス変換
InverseLaplaceTransform[expr,s,t]
式 expr の逆ラプラス変換
一次元ラプラス変換
関数 のラプラス変換は， で与えられる． の逆ラプラス変換は，適当な の値に対して で与えられる．
簡単なラプラス変換を求める：
Wolfram Language code: LaplaceTransform[t ^ 4 Sin[t], t, s]
逆ラプラス変換を求める：
Wolfram Language code: InverseLaplaceTransform[%, s, t]
簡単な変換でも特殊関数が必要になることがしばしばある：
Wolfram Language code: LaplaceTransform[1 / (1 + t ^ 2), t, s]
結果にはマイヤーのG関数が含まれる：
Wolfram Language code: LaplaceTransform[1 / (1 + t ^ 3), t, s]
InverseLaplaceTransformはもとの関数を返す：
Wolfram Language code: InverseLaplaceTransform[%, s, t]
このベッセル関数のラプラス変換は基本的な関数のみを含む：
Wolfram Language code: LaplaceTransform[BesselJ[n, t], t, s]
ラプラス変換は，本質的に微積分を代数演算に変換するという特性がある．従って，一般に微分方程式で支配される系に広く使用される．
ラプラス変換を施すと，積分は の乗算となる：
Wolfram Language code: LaplaceTransform[Integrate[f[u], {u, 0, t}], t, s]
LaplaceTransform[expr,{t1,t2,…},{s1,s2,…}]
式 expr の多次元ラプラス変換
InverseLaplaceTransform[expr,{s1,s2,…},{t1,t2,…}]
式 expr の多次元逆ラプラス変換
多次元ラプラス変換

フーリエ変換

FourierTransform[expr,t,ω]
式 expr のフーリエ変換
InverseFourierTransform[expr,ω,t]
式 expr の逆フーリエ変換
一次元フーリエ変換
この場合，積分変換はHeavisideThetaのような「一般化された関数」を含む結果を返すことがある：
Wolfram Language code: FourierTransform[1 / (1 + t ^ 4), t, ω]
逆変換を見付ける：
Wolfram Language code: InverseFourierTransform[%, ω, t]
Wolfram言語では関数 のフーリエ変換は，デフォルトでは で定義される．の逆フーリエ変換は同様に として定義される．
科学技術分野では，分野によりフーリエ変換の定義に異なったさまざまな規約が用いられる．Wolfram言語のFourierParametersオプションで任意の規約を選択することができる．
共通規約
設定
フーリエ変換
逆フーリエ変換
Wolfram言語デフォルト
{0,1}
純粋数学
{1,-1}
古典物理学
{-1,1}
現代物理学
{0,1}
システム工学
{1,-1}
信号処理
{0,-2Pi}
一般の場合
{a,b}
さまざまな規約のFourierParametersの典型的な設定
パラメータとしてデフォルトを選択をしたフーリエ変換である：
Wolfram Language code: FourierTransform[Exp[-t ^ 2], t, ω]
信号処理で通常用いられるパラメータを選択した同じフーリエ変換である：
Wolfram Language code: FourierTransform[Exp[-t ^ 2], t, ω, FourierParameters -> {0, -2 Pi}]
FourierSinTransform[expr,t,ω]
フーリエ正弦変換
FourierCosTransform[expr,t,ω]
フーリエ余弦変換
InverseFourierSinTransform[expr,ω,t]
逆フーリエ正弦変換
InverseFourierCosTransform[expr,ω,t]
逆フーリエ余弦変換
フーリエ正弦，余弦変換
フーリエ変換を使う分野によっては複素指数を全く使用しない方が便利なことがある．フーリエ正弦および余弦変換では，の代りにそれぞれとを積分し，との代りに0からの範囲で積分する．
のフーリエ正弦，余弦変換である：
Wolfram Language code: {FourierSinTransform[Exp[-t], t, ω], FourierCosTransform[Exp[-t], t, ω]}
FourierTransform[expr,{t1,t2,…},{ω1,ω2,…}]
式 expr の多次元フーリエ変換
InverseFourierTransform[expr,{ω1,ω2,…},{t1,t2,…}]
式 expr の多次元逆フーリエ変換
FourierSinTransform[expr,{t1,t2,…},{ω1,ω2,…}]
,
FourierCosTransform[expr,{t1,t2,…},{ω1,ω2,…}]
式 expr の多次元正弦，余弦フーリエ変換
InverseFourierSinTransform[expr,{ω1,ω2,…},{t1,t2,…}]
,
InverseFourierCosTransform[expr,{ω1,ω2,…},{t1,t2,…}]
式 expr の多次元正弦および余弦逆フーリエ変換
多次元フーリエ変換
二次元フーリエ変換を評価する：
Wolfram Language code: FourierTransform[(u v) ^ 2 Exp[-u ^ 2 - v ^ 2], {u, v}, {a, b}]
逆フーリエ変換を施す：
Wolfram Language code: InverseFourierTransform[%, {a, b}, {u, v}]

Z変換

ZTransform[expr,n,z]
式 expr のZ変換
InverseZTransform[expr,z,n]
式 expr の逆Z変換
Z変換
関数 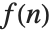のZ変換は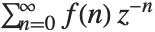， で与えられる．の逆Z変換は，線積分 で与えられる．Z変換は離散化されたラプラス変換に相当する．特にデジタル信号処理や制御理論等で差分方程式の解法に幅広く用いられている．これらは組合せ理論および数論でよく使用される生成関数を作成するものと考えられる．
のZ変換を計算する：
Wolfram Language code: ZTransform[2 ^ -n, n, z]
逆Z変換を施す：
Wolfram Language code: InverseZTransform[%, z, n]
の生成関数は指数関数である：
Wolfram Language code: ZTransform[1 / n!, n, z]
一般化された関数と関連操作
実際問題では多くの場合，ある一定量のものが微小領域に集中しているような極限を考慮すると便利なことがある．微積分学で扱われる通常の数学的な関数では，このような極限を直ちに表すことができない．しかし，超関数を導入することによって，これらの極限を積分や他の計算形式で表すことができる．
DiracDelta[x]
ディラック(Dirac)のデルタ関数
HeavisideTheta[x]
の場合は0，の場合は1のヘビサイド(Heaviside)のシータ関数
ディラックのデルタ関数とヘビサイドのシータ関数
の周りに集中した関数：
Wolfram Language code: Plot[Sqrt[50 / Pi] Exp[-50 x ^ 2], {x, -2, 2}, PlotRange -> All]
が大きくなるにつれ，関数は次第に集中してくる：
Wolfram Language code: Plot[Evaluate[Sqrt[n / Pi] Exp[-n x ^ 2] /. n -> {1, 10, 100}], {x, -2, 2}, PlotRange -> All]
なら積分は常に1に等しくなる：
Wolfram Language code: Integrate[Sqrt[n / Pi] Exp[-n x ^ 2], {x, -Infinity, Infinity}, Assumptions -> n > 0]
を無限大にした場合の関数の極限は，ディラックのデルタ関数となり，積分は再び1になる：
Wolfram Language code: Integrate[DiracDelta[x], {x, -Infinity, Infinity}]
DiracDeltaは 以外のすべての実数の点で0に評価する：
Wolfram Language code: Table[DiracDelta[x], {x, -3, 3}]
積分内にデルタ関数を組み入れると，デルタ関数の引数がゼロになる離散的な点で，被積分関数の値を抽出できる効果がある．
関数fを引数2で抽出する：
Wolfram Language code: Integrate[DiracDelta[x - 2] f[x], {x, -4, 4}]
少し複雑な例を示す：
Wolfram Language code: Integrate[DiracDelta[x ^ 2 - x - 1], {x, 0, 2}]
これにより，積分領域で の零点の個数を数えることができる：
Wolfram Language code: Integrate[DiracDelta[Cos[x]], {x, -30, 30}]
ヘビサイド関数HeavisideTheta[x]はデルタ関数の不定積分である．これは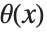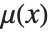，，，および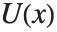等で表される．一般化された関数として，ヘビサイド関数は積分内でのみ定義される．この点で，区分関数である単位階段関数UnitStep[x]と区別される．
デルタ関数の不定積分はヘビサイドのシータ関数である：
Wolfram Language code: Integrate[DiracDelta[x], x]
この積分の値は が区間内にあるかどうかによる：
Wolfram Language code: Integrate[f[x] DiracDelta[x - a], {x, -2, 2}, Assumptions -> a ∈ Reals]
DiracDeltaとHeavisideThetaは，積分変換でよく現れる．
定数関数のフーリエ変換はデルタ関数である：
Wolfram Language code: FourierTransform[1, t, ω]
のフーリエ変換には2つのデルタ関数の和が含まれる：
Wolfram Language code: FourierTransform[Cos[t], t, ω]
ディラックのデルタ関数はDSolveで使用され，線形および他の微分方程式で表された系のインパルス応答やグリーン(Green)関数を見付けるのに使われる．
でインパルスを受ける調和振動子の挙動を示す：
Wolfram Language code: DSolve[{x''[t] + r x[t] == DiracDelta[t], x[0] == 0, x'[0] == 1}, x[t], t] /. {HeavisideTheta[0] -> 1}
DiracDelta[x1,x2,…]
多次元ディラックのデルタ関数
HeavisideTheta[x1,x2,…]
多次元ヘビサイドのシータ関数
多次元のディラックのデルタ関数とヘビサイドのシータ関数
多次元の一般化された関数は，本質的に一変量の一般化された関数の積である．
これは，多次元ヘビサイド関数の導関数である：
Wolfram Language code: D[HeavisideTheta[x, y, z], x]
多次元ディラックのデルタ関数に関連するものとして離散デルタとクロネッカーのデルタの2つの整数関数がある．離散デルタ はすべての ならば1であり，その他の場合はゼロである．クロネッカーのデルタ 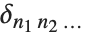は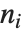， がすべて等しければ1であり，その他の場合はゼロである．
DiscreteDelta[n1,n2,…]
離散デルタ
KroneckerDelta[n1,n2,…]
クロネッカーのデルタ
整数デルタ関数