微积分
| D[f,x] | 偏导数 |
| D[f,x,y,…] | 多重导数 |
| D[f,{x,n}] | n 阶导数 |
| D[f,x,NonConstants->{v1,v2,…}] |
| D[f,{{x1,x2,…}}] | 标量函数 |
| D[f,{{x1,x2,…},2}] | f 的 Hessian 矩阵 |
| D[f,{{x1,x2,…},n}] | n 阶泰勒级数的系数 |
| D[{f1,f2,…},{{x1,x2,…}}] | 向量函数 f 的 Jacobian 矩阵 |
| Dt[f] | 全微分 df |
| Dt[f,x] | 全导数 |
| Dt[f,x,y,…] | 多重全导数 |
| Dt[f,x,Constants->{c1,c2,…}] | 全导数,ci 为常数 (即 dci=0) |
| y/:Dt[y,x]=0 | 设 |
| SetAttributes[c,Constant] | 在所有情况下将 c 定义为常数 |
在 Wolfram 系统中,D[f,x] 给出了偏导数,假定其他所有变量与 x 无关. Dt[f,x] 给出全导数,假定所有都变量依赖于 x. 在这两种情况下,都可以添加参数以提供有关依赖关系的更多信息.
标准数学符号  实际上是
实际上是 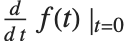 的简写,其中
的简写,其中 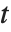 是“虚拟变量”. 同样,
是“虚拟变量”. 同样,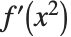 是
是 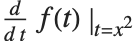 的简写. 如符号
的简写. 如符号 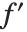 所示,对象
所示,对象 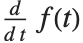 实际上可被视为“纯函数”,可以通过选择参数
实际上可被视为“纯函数”,可以通过选择参数 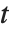 对其进行计算. 可以将微分运算视为作用在函数
对其进行计算. 可以将微分运算视为作用在函数 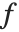 上以给出一个新函数,通常称为
上以给出一个新函数,通常称为 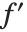 .
.
在 Wolfram 系统中,就像在数学的某些分支中一样,是将微分视为作用于函数上,而不是表达式. 需要的是一个运算,接受函数 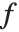 ,并给出求导函数
,并给出求导函数 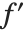 . 像这样的作用于函数而不是变量的运算在数学上称为运算符.
. 像这样的作用于函数而不是变量的运算在数学上称为运算符.
Wolfram 系统中的对象 f' 是将微分算子应用于函数 f 的结果. 实际上 f' 的完整格式是 Derivative[1][f]. Derivative[1] 是 Wolfram 系统的微分算子.
因为 Derivative 只指定关于每个 "slot" 进行几次微分,所以求导的顺序无关:
对象 f' 实际上类似于 Wolfram 系统中的任何其他函数. 可以对任何参数计算函数,可以使用 Wolfram 系统的标准运算符 /. 改变参数. (如果在微分过程中引入了显式虚拟变量,则不能这样操作.)
函数 f' 完全由函数 f 的形式确定. 对 f[x_] 之类的对象的定义不能立即应用于 f'[x] 之类的表达式. 问题在于 f'[x] 的完整格式为 Derivative[1][f][x],其中没有包含与模式 f[x_] 明确匹配的任何内容. 此外,出于许多原因,函数 f' 自身表示的这种形式可以带来很多方便,不必将其应用于任何参数.
Wolfram 系统尝试找到代表对象 f' 的显式形式的纯函数. 当 Wolfram 系统获得与 Derivative[1][f] 类似的表达式时,实际上是将其转换成显式形式 D[f[#],#]&,然后尝试计算导数. 对于显式形式,Wolfram 系统可以立即使用为 f[x_] 这样的对象定义的值.如果 Wolfram 系统成功地完成了导数运算,它将返回显式的纯函数结果. 如果不成功,则保留原始的 f' 形式.
下面以纯函数形式给出了 Tan 的导数:
| f'[x_]:=rhs | 定义 f 的一阶导数 |
| Derivative[n][f][x_]:=rhs | 定义 f 的 n 阶导数 |
| Derivative[m,n,…][g][x_,_,…]:=rhs | |
定义 g 关于各个参数的导数 | |
Wolfram 语言知道如何执行绝大多数可以通过标准数学函数完成的积分. 但是,应该知道,即使一个被积函数可能只包含相当简单的函数,但它的积分却可能涉及非常复杂的函数,或者可能根本无法用标准数学函数表示.
下面的积分涉及 Erf:
| Integrate[f,x] | 不定积分 ∫f dx |
| Integrate[f,x,y] | 多重积分 ∫dx dy f |
| Integrate[f,{x,xmin,xmax}] | 定积分 |
| Integrate[f,{x,xmin,xmax},{y,ymin,ymax}] | |
多重积分 | |
Wolfram 语言函数 Integrate[f,x] 给出不定积分 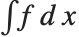 . 可以将不定积分运算视为微分的逆运算. 如果对 Integrate[f,x] 的结果进行微分,则始终会得到数学上等于原始表达式 f 的结果.
. 可以将不定积分运算视为微分的逆运算. 如果对 Integrate[f,x] 的结果进行微分,则始终会得到数学上等于原始表达式 f 的结果.
可以将一个任意常数添加到不定积分中,并且仍然获得相同的导数. Integrate 只是给出一个具有要求的导数的表达式:
用 ArcTan 给出的积分:
用 ArcTanh 给出的积分:
Integrate 选择使用两个形式中较简单的一种:
但是,对于此积分,则需要特殊函数 LogIntegral:
在最方便的情况下,可以用初等函数(例如指数函数,对数函数和三角函数)完成积分. 实际上,如果给出只涉及此类初等函数的被积函数,则 Integrate 的重要功能之一就是,如果相应的积分可以用初等函数表示,那么 Integrate 总是会成功地给出结果.
可以使用 Piecewise 系统地完成这样的积分:
除了初等函数,Integrate 还包括了用于处理特殊函数的大量算法. 有时,它将用于初等函数的过程直接进行推广. 但更常见的策略是先尝试将被积函数写成以某些复杂的特殊函数表示的形式,然后执行此操作以尝试将这些复杂的函数简化为熟悉的函数.
特别是如果引入了自定义的新数学函数,则可能需要教 Wolfram 语言新的积分形式. 可以通过对 Integrate 进行适当的定义来做到这一点.
在进行微分时,链式法则允许将所有导数简化为标准形式,以 Wolfram 语言中的 Derivative 表示. 但是对于积分,不存在类似的标准格式,因此,经常必须对同一积分的多个不同版本进行定义. 很少能通过 Integrate 自动完成变量的更改和其他转换.
| Integrate[f,{x,xmin,xmax},PrincipalValue->True] | |
定积分的柯西主值 | |
选项名称
|
默认值
| |
| GenerateConditions | Automatic | 是否生成显式条件 |
| Assumptions | $Assumptions | 假定的参数之间的关系 |
Integrate 的选项.
这里的 If 给出了积分收敛的条件:
可以使用 Wolfram 语言函数 DSolve 求常微分方程的符号解.
Wolfram 语言函数 DSolve 返回的结果是一个函数的规则列表. 问题是这些函数如何被表示的. 如果令 DSolve 关于 y[x] 求解,那么 DSolve 将返回 y[x] 的规则. 某些情况下,这个规则正是所需要的. 但这个规则本身并不给出 y'[x] 或 y[0] 的值. 因此,多数情况下,最好让 DSolve 关于 y 本身求解,而不是关于 y[x] 求解. 这种情况下,DSolve 返回的是将 y 作为纯函数的规则,如“纯函数”中所讨论的那样.
将解代入原方程得到 True:
在标准数学表示法中,通常通过明确引入“虚拟变量”表示函数的自变量的方法来表示微分方程的解. 如果用户需要的仅仅是符号形式的解,那么引入虚拟变量可能很方便. 但是,如果打算将解用于其它运算中,那么最好是得到不带虚拟变量的纯函数形式的解. 注意,这种形式虽然易于用 Wolfram 语言表示,但在标准数学表示法中没有相应的形式.
| DSolve[{eqn1,eqn2,…},{y1,y2,…},x] | |
求解微分方程组 | |
默认情况下,这些常数被命名为 C[n],其中 n 从 1 开始,随着调用 DSolve 的次数而递增. 通过设置选项 GeneratedParameters 可以覆盖这个选择. 你所给的任何函数被应用于每一个相继的 n 值,从而得到每次调用 DSolve 所用的常数.
但如果超过一个微分方程,或包含高阶导数,这将不再成立. 但是,仍然可以使用“特殊函数”中的各种特殊函数来求解一些简单的二阶线性微分方程. 事实上,在历史上许多特殊函数就是为了表示这种方程的解而引入的.
对于二阶以上的方程,即便是求解相当简单的线性微分方程所需的函数种类也极为复杂. 对于三阶方程,有时可使用广义 Meijer G 函数 MeijerG,但对于四阶或更高阶的方程,绝对没有标准的数学函数能满足要求,除非是很特殊的情况.
对于非线性微分方程,仅有一些特殊情形能用标准数学函数求解. 尽管如此,DSolve 包含了相当通用的程序,能够处理几乎所有在标准参考书中能找到解的非线性微分方程.
在实际应用中,建立含有分段函数的微分方程通常很方便. 可以使用 DSolve 来求这种方程的符号解.
DSolve 不仅能求解仅有一个自变量的常微分方程,也能求解有两个或多个自变量的偏微分方程.
偏微分方程涉及的数学基础比常微分方程要复杂得多. 一个特征是:常微分方程的通解仅包含任意常数,而偏微分方程的通解必须包含任意函数. 实际上,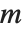 元偏微分方程的通解,包含
元偏微分方程的通解,包含  元的任意函数. 默认情况下,DSolve 将这些函数命名为 C[n].
元的任意函数. 默认情况下,DSolve 将这些函数命名为 C[n].
拉普拉斯变换
| LaplaceTransform[expr,t,s] | expr 的拉普拉斯变换 |
| InverseLaplaceTransform[expr,s,t] | expr 的拉普拉斯逆变换 |
InverseLaplaceTransform 返回原函数:
| LaplaceTransform[expr,{t1,t2,…},{s1,s2,…}] | |
expr 的多维拉普拉斯变换 | |
| InverseLaplaceTransform[expr,{s1,s2,…},{t1,t2,…}] | |
expr 多维拉普拉斯逆变换 | |
傅立叶变换
| FourierTransform[expr,t,ω] | expr 的傅立叶变换 |
| InverseFourierTransform[expr,ω,t] | expr 的傅立叶逆变换 |
在不同的科学和技术领域,通常使用不同的约定来定义傅立叶变换. Wolfram 语言中的选项 FourierParameters 允许用户选择所需的任何约定.
常见约定
|
设置
|
傅立叶变换
|
傅立叶逆变换
|
Wolfram 语言默认定义 |
{0,1}
| ||
纯数学 |
{1,-1}
| ||
经典物理学 |
{-1,1}
| ||
现代物理学 |
{0,1}
| ||
系统工程 |
{1,-1}
| ||
信号处理 |
{0,-2Pi}
| ||
一般情形 |
{a,b}
|
各种约定下 FourierParameters 的常见设置.
| FourierSinTransform[expr,t,ω] | 傅立叶正弦变换 |
| FourierCosTransform[expr,t,ω] | 傅立叶余弦变换 |
| InverseFourierSinTransform[expr,ω,t] | |
傅立叶正弦逆变换 | |
| InverseFourierCosTransform[expr,ω,t] | |
傅立叶余弦逆变换 | |
| FourierTransform[expr,{t1,t2,…},{ω1,ω2,…}] | |
expr 的多维傅立叶变换 | |
| InverseFourierTransform[expr,{ω1,ω2,…},{t1,t2,…}] | |
expr 的多维傅立叶逆变换 | |
| FourierSinTransform[expr,{t1,t2,…},{ω1,ω2,…}]
,
FourierCosTransform[expr,{t1,t2,…},{ω1,ω2,…}] | |
expr 的多维傅立叶正弦和余弦变换 | |
| InverseFourierSinTransform[expr,{ω1,ω2,…},{t1,t2,…}]
,
InverseFourierCosTransform[expr,{ω1,ω2,…},{t1,t2,…}] | |
expr 的多维傅立叶正弦和余弦逆变换 | |
Z 变换
| ZTransform[expr,n,z] | expr 的 Z 变换 |
| InverseZTransform[expr,z,n] | expr 的 Z 逆变换 |
函数 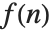 的 Z 变换由
的 Z 变换由 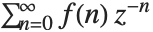 给出.
给出.  的 Z 逆变换由围道积分
的 Z 逆变换由围道积分  给出. Z 变换实际上是离散版本的拉普拉斯变换,被广泛应用于求解微分方程,特别是在数字处理和控制理论领域. 可将其视为常常用于组合数学和数论中的生成母函数.
给出. Z 变换实际上是离散版本的拉普拉斯变换,被广泛应用于求解微分方程,特别是在数字处理和控制理论领域. 可将其视为常常用于组合数学和数论中的生成母函数.
| DiracDelta[x] | Dirac delta 函数 |
| HeavisideTheta[x] | Heaviside theta 函数 |
Heaviside 函数 HeavisideTheta[x] 是 delta 函数的不定积分. 它有多种表示法: 、
、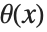 、
、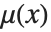 和
和 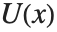 . 作为广义函数,Heaviside 函数只在积分内部有定义. 这与单位跃阶函数 UnitStep[x] 不同,后者是一个分段函数.
. 作为广义函数,Heaviside 函数只在积分内部有定义. 这与单位跃阶函数 UnitStep[x] 不同,后者是一个分段函数.
可将 Dirac delta 函数用在 DSolve 中,求由线性方程和某些其他微分方程表示的系统的冲激响应或格林函数.
| DiracDelta[x1,x2,…] | 多维 Dirac delta 函数 |
| HeavisideTheta[x1,x2,…] | 多维 Heaviside theta 函数 |
与多维 Dirac delta 函数相关的是两个整数函数:离散 delta 函数和 Kronecker delta 函数. 如果所有的  ,离散 delta 函数
,离散 delta 函数  为 1,否则为零. 如果所有的
为 1,否则为零. 如果所有的 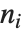 都相等,Kronecker delta 函数
都相等,Kronecker delta 函数 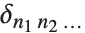 为 1,否则为零.
为 1,否则为零.
| DiscreteDelta[n1,n2,…] | 离散 delta 函数 |
| KroneckerDelta[n1,n2,…] | Kronecker delta 函数 |