AdjacencyGraph
AdjacencyGraph[amat]
给出邻接矩阵为 amat 的图.
AdjacencyGraph[{v1,v2,…},amat]
给出顶点为 vi、邻接矩阵为 amat 的图.
更多信息和选项

- AdjacencyGraph[amat] 等价于 AdjacencyGraph[{1,2,…,n},amat],其中 amat 维度为
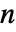 ×
× .
. - AdjacencyGraph 采用与 Graph 相同的选项.
- 选项 DirectedEdges 可以用来控制是否构建一个无向图或者有向图.
- DirectedEdges 的下列选项可以用于 AdjacencyGraph 中:
-
Automatic 如果 amat 是对称的,则构建一个无向图 True 构建一个有向图 False 构建一个无向图

所有选项的列表
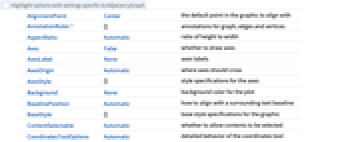
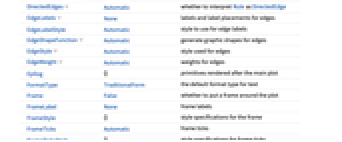
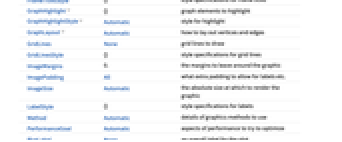

背景
- AdjacencyGraph 根据无向或有向图的邻接矩阵构建一个图. 邻接矩阵是一个方阵,其行和列对应于图的顶点而其中的元素 aij 是非负整数,标明的是从顶点 vi 到顶点 vj 的(有向)边的数目. 对角线元素不为零的邻接矩阵意味着图有自环.
- 选项 DirectedEdges(可能的值为 Automatic、True 或 False)可被用于控制构建的是无向还是有向图. 默认情况下,若输入矩阵是对称的,则 AdjacencyGraph 返回无向图,否则返回有向图.
- AdjacencyGraph 与 Graph 有相同的选项(例如 EdgeStyle、VertexStyle、EdgeLabels、VertexLabels、GraphLayout、VertexCoordinates 等等). AdjacencyGraph 并不考虑图的权重,所以要从加权邻接矩阵构建图的话必须使用 WeightedAdjacencyGraph.
- AdjacencyList 返回给定顶点 vi 的相邻顶点的列表并因此对应于邻接矩阵第 i
 列(若是无向图则是第 i
列(若是无向图则是第 i 行)非零元素的位置列表. 任何图的整个邻接矩阵(包括用 AdjacencyGraph 构建的)都可以用 AdjacencyMatrix 返回得到. IncidenceGraph 用关联矩阵表示代替邻接矩阵来构造图.
行)非零元素的位置列表. 任何图的整个邻接矩阵(包括用 AdjacencyGraph 构建的)都可以用 AdjacencyMatrix 返回得到. IncidenceGraph 用关联矩阵表示代替邻接矩阵来构造图.
范例
打开所有单元关闭所有单元范围 (7)
选项 (83)
DirectedEdges (3)
EdgeLabels (7)
使用符号位置信息的 Placed 来控制沿着一条边的标签位置:
通过 Tooltip 和 StatusArea 的值,使用自动标签:
EdgeShapeFunction (6)
获取 EdgeShapeFunction 的内置设置列表:
EdgeShapeFunction 可以与 EdgeStyle 合起来使用:
EdgeShapeFunction 具有比 EdgeStyle 更高的优先级:
GraphHighlightStyle (2)
GraphLayout (5)
VertexCoordinates 重载 GraphLayout 坐标:
通过一个布局算法,利用 AbsoluteOptions 提取计算所得的 VertexCoordinates:
VertexCoordinates (3)
使用 AbsoluteOptions 提取所得的顶点坐标:
VertexCoordinates 具有比 GraphLayout 更高的优先级:
VertexLabels (13)
使用具有符号位置信息的 Placed 来控制标签位置,包括内部位置:
或者 StatusArea:
VertexShape (5)
将任意 Graphics、Image 或者 Graphics3D 作为顶点形状使用:
VertexShape 可以与 VertexSize 合起来使用:
VertexShape 不受 VertexStyle 影响:
VertexShapeFunction 具有比 VertexShape 更高的优先级:
VertexShapeFunction (10)
获取 VertexShapeFunction 的内置设置列表:
利用 VertexShapeFunction 在 "Basic" 集合中的内置设置:
使用 VertexShapeFunction 在 "Rounded" 集合中的内置设置:
使用 VertexShapeFunction 在 "Concave" 集合中的内置设置:
VertexShapeFunction 可以与 VertexStyle 合起来使用:
VertexShapeFunction 具有比 VertexStyle 更高的优先级:
VertexShapeFunction 可以与 VertexSize 合起来使用:
VertexShapeFunction 具有比 VertexShape 更高的优先级:
VertexSize (8)
VertexSize 可以与 VertexShapeFunction 合起来使用:
VertexSize 可以与 VertexShape 合起来使用:
VertexStyle (5)
VertexShapeFunction 可以与 VertexStyle 合起来使用:
VertexShapeFunction 具有比 VertexStyle 更高的优先级:
VertexStyle 可以与 BaseStyle 合起来使用:
VertexStyle 具有比 BaseStyle 更高的优先级:
VertexShape 不受 VertexStyle 影响:
应用 (2)
属性和关系 (6)
文本
Wolfram Research (2010),AdjacencyGraph,Wolfram 语言函数,https://reference.wolfram.com/language/ref/AdjacencyGraph.html.
CMS
Wolfram 语言. 2010. "AdjacencyGraph." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/AdjacencyGraph.html.
APA
Wolfram 语言. (2010). AdjacencyGraph. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AdjacencyGraph.html 年