BernoulliDistribution
確率母数が p のベルヌーイ(Bernoulli)分布を表す.
詳細
- BernoulliDistributionはコイントスの分布あるいはベルヌーイの試行としても知られている.
- BernoulliDistributionは確率
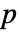 で
で 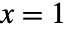 を,確率
を,確率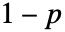 では
では 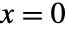 を返す. »
を返す. » - BernoulliDistributionでは,確率母数 p は無次元量でよい. »
- BernoulliDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- BernoulliDistribution[p]は,実数上で定義される離散統計分布を表す.母数 p は
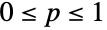 を満足する確率母数を表す.ベルヌーイ分布はコイントス分布あるいはベルヌーイ試行の分布と呼ばれることがある.この分布の確率密度関数(PDF)は,
を満足する確率母数を表す.ベルヌーイ分布はコイントス分布あるいはベルヌーイ試行の分布と呼ばれることがある.この分布の確率密度関数(PDF)は,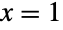 では値 p,
では値 p,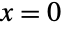 では
では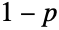 を返し,その他のすべての実数について評価すると0になる.
を返し,その他のすべての実数について評価すると0になる. - ベルヌーイ分布はスイスの数学者であるJacob Bernoulliの名前に因んで命名された.この分布は,(公正な,あるいは不正な)コインをトスするという単純な動作のモデル化のためのものである.伝統的に,p は実験が「成功する」確率(1は成功した実験を表す),
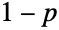 は実験が「失敗する」確率(0は失敗した実験を表す)であると考えられる.コイントスの類推から,1は表を表すことが多く,0は裏を表すことが多い.値
は実験が「失敗する」確率(0は失敗した実験を表す)であると考えられる.コイントスの類推から,1は表を表すことが多く,0は裏を表すことが多い.値 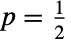 は公正なコインのトスに相当する.非常に簡単に定義されているのにもかかわらず,ベルヌーイ分布は,確率におけるベルヌーイ列,測度論におけるベルヌーイ測度,力学系におけベルヌーイ系等の,より複雑な数多くの他の数学概念の基礎になっていることがよくある.確率過程の研究の中で,ベルヌーイ分布は,いわゆるベルヌーイ過程(BernoulliProcess),つまり,1つ1つが独立同ベルヌーイ分布に従う(有限あるいは無限の)確率変数の列からなる離散時間確率過程のきっかけにもなっている.さらに,独立した結果の確率についてのよく定義された二分法を示す数多くの現実世界の出来事が,ベルヌーイ過程としてモデル化できる.例には,1つの(公正な)サイコロで特定の値が出る確率や,欠陥率が生産スケールには依存しない場合の欠陥製品の数が含まれる.
は公正なコインのトスに相当する.非常に簡単に定義されているのにもかかわらず,ベルヌーイ分布は,確率におけるベルヌーイ列,測度論におけるベルヌーイ測度,力学系におけベルヌーイ系等の,より複雑な数多くの他の数学概念の基礎になっていることがよくある.確率過程の研究の中で,ベルヌーイ分布は,いわゆるベルヌーイ過程(BernoulliProcess),つまり,1つ1つが独立同ベルヌーイ分布に従う(有限あるいは無限の)確率変数の列からなる離散時間確率過程のきっかけにもなっている.さらに,独立した結果の確率についてのよく定義された二分法を示す数多くの現実世界の出来事が,ベルヌーイ過程としてモデル化できる.例には,1つの(公正な)サイコロで特定の値が出る確率や,欠陥率が生産スケールには依存しない場合の欠陥製品の数が含まれる. - RandomVariateを使ってベルヌーイ分布から,1つあるいは複数の機械精度あるいは任意精度の擬似乱数変量を得ることができる.Distributed[x,BernoulliDistribution[p]](より簡略すると xBernoulliDistribution[p])を使って,確率変数 x が,ベルヌーイ分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[BernoulliDistribution[p],x]およびCDF[BernoulliDistribution[p],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.これらの数量はDiscretePlotを使って可視化することができる.
- DistributionFitTestを使って,与えられたデータ集合がベルヌーイ分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックベルヌーイ分布を推定することが,FindDistributionParametersを使ってデータをベルヌーイ分布にフィットすることができる.ProbabilityPlotを使って記号ベルヌーイ分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号ベルヌーイ分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたベルヌーイ分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってベルヌーイ分布を含む高次元分布を構築することが,ProductDistributionを使ってベルヌーイ分布を含む独立成分分布の結合分布を計算することができる.
- BernoulliDistributionは他の多くの確率分布と関連している.例えば,BernoulliDistribution[p]は一回のBinomialDistribution[1,p]に等しい.つまり,PDF[BernoulliDistribution[p],k]はPiecewise[Table[{PDF[BinomialDistribution[1,p],l],kl},{l,0,1}]]と同じである.同様に,共通の成功率が p である n 個の独立したベルヌーイ変数の和はBinomialDistribution[n,p]でモデル化される.加えて,ベルヌーイ独立分布に従う確率変数集合から浮かび出る数多くの自然発生的な数量は,よく知られる多の分布に従ってモデル化できることがある.例えば,BernoulliDistribution[p]に従って分布するデータ点の最初の n 個における成功数はBinomialDistribution[n,p]に従って分布しているのに対し,1回(あるいは r 回)の成功を得るための試行回数はGeometricDistribution[p](あるいは NegativeBinomialDistribution[r,p])に従って分布している.
例題
すべて開くすべて閉じるスコープ (8)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
無次元のQuantityを使ってBernoulliDistributionを定義する:
アプリケーション (6)
六面のサイコロを振って6が出る確率はベルヌーイ分布としてモデル化できる:
6の目が出る場合だけに関心があるとしてサイコロ投げのシミュレーションをしてみる:
製造される電球10個につき1個の割合で不良品が出るとして,100個の電球を製造するシミュレーションを行う:
1枚1ドルで10枚発売する宝くじがある.その中で当選するのは毎回1枚だけである.ある賭博者が宝くじに5ドル使うとする.この賭博者が5つの宝くじでそれぞれ1枚ずつ,合計5枚買った場合の勝率を求める:
この男の勝率は1つの宝くじでまとめて5枚買った場合の方が高い:
ある光通信システムでは送信された光が受信装置で電流を生ずる.電子の数は光のタイプによってポアソン分布と他の分布の母数混合に従う.ソースが強度 ![]() のコヒーレントレーザー光を使う場合,電子の数の分布はポアソン分布になる:
のコヒーレントレーザー光を使う場合,電子の数の分布はポアソン分布になる:
これはPoissonDistributionである:
ソースで熱照明が使われている場合,ポアソン母数は![]() 母数でExponentialDistributionに従い,電子数の分布は次のようになる:
母数でExponentialDistributionに従い,電子数の分布は次のようになる:
特性と関係 (4)
考えられる問題 (2)
テキスト
Wolfram Research (2007), BernoulliDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/BernoulliDistribution.html (2016年に更新).
CMS
Wolfram Language. 2007. "BernoulliDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BernoulliDistribution.html.
APA
Wolfram Language. (2007). BernoulliDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BernoulliDistribution.html
