BernoulliDistribution
表示概率参数为 p 的伯努利分布.
更多信息
- BernoulliDistribution 也称为硬币投掷分布或者伯努利试验.
- 在 BernoulliDistribution 中,
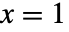 的概率为
的概率为 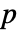 ,
,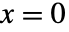 的概率为
的概率为 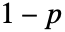 . »
. » - BernoulliDistribution 允许概率参数 p 为无量纲的量. »
- BernoulliDistribution 可以同诸如 Mean、CDF 以及 RandomVariate 等函数一起使用. »
背景
- BernoulliDistribution[p] 表示定义在实数上的离散统计分布,其中参数 p 是满足
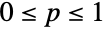 的概率参数. 伯努利分布有时也被称为抛硬币分布或伯努利试验的分布. 它具有一个离散概率密度函数( PDF),该函数在
的概率参数. 伯努利分布有时也被称为抛硬币分布或伯努利试验的分布. 它具有一个离散概率密度函数( PDF),该函数在 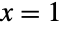 时,返回值 p ,当
时,返回值 p ,当 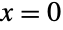 时,返回值
时,返回值 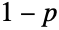 ,对于所有其它实数返回0.
,对于所有其它实数返回0. - 伯努利分布为纪念瑞士科学家雅各布·伯努利(Jacob Bernoulli)而命名,旨在模拟抛掷(公平或非公平)硬币的简单动作. 传统上,p 被认为是与实验“成功”的概率(1代表成功的实验),而
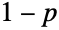 为“失败”的概率(0代表失败的实验).在投硬币的类比中,1通常表示正面,而反面由0表示. 值
为“失败”的概率(0代表失败的实验).在投硬币的类比中,1通常表示正面,而反面由0表示. 值 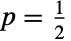 对应着抛掷一枚公平硬币. 尽管定义很简单,伯努利分布是其他一些往往更复杂的数学概念的基础,包括概率中的伯努利序列,测度论中的伯努利测度,以及在动态系统中的伯努利方案. 在随机过程的研究范围内,伯努利分布还是伯努利过程(BernoulliProcess)的背后动力。所谓伯努利过程,是由(有限个或无限个)随机变量序列组成的离散时间随机过程,其中每个变量都是独立且相同的伯努利分布. 此外,许多现实世界的情景,如果其独立结果的可能性呈现出良好定义的二分法,均可以看作是伯努利过程. 实例包括投掷一个(公平)骰子时得到某一特定值的概率,和缺陷率独立于生产规模时,有缺陷的产品的数量.
对应着抛掷一枚公平硬币. 尽管定义很简单,伯努利分布是其他一些往往更复杂的数学概念的基础,包括概率中的伯努利序列,测度论中的伯努利测度,以及在动态系统中的伯努利方案. 在随机过程的研究范围内,伯努利分布还是伯努利过程(BernoulliProcess)的背后动力。所谓伯努利过程,是由(有限个或无限个)随机变量序列组成的离散时间随机过程,其中每个变量都是独立且相同的伯努利分布. 此外,许多现实世界的情景,如果其独立结果的可能性呈现出良好定义的二分法,均可以看作是伯努利过程. 实例包括投掷一个(公平)骰子时得到某一特定值的概率,和缺陷率独立于生产规模时,有缺陷的产品的数量. - RandomVariate 可用于给出一个或多个机器精度或任意精度的伯努利分布伪随机变元. Distributed[x,BernoulliDistribution[p]],更简洁的表示为 xBernoulliDistribution[p],可用于论断随机变量 x 服从伯努利分布. 然后这类论断可用于诸如 Probability、NProbability、Expectation 和 NExpectation 等函数中.
- 概率密度和累积分布函数可以通过使用 PDF[BernoulliDistribution[p],x] 和CDF[BernoulliDistribution[p],x] 给出. 均值、中位数、方差、原始矩和中心矩可以分别使用 Mean、Median、Variance、Moment 和 CentralMoment 计算. 这些量值可以使用 DiscretePlot 进行可视化.
- DistributionFitTest 可用于检验给定的数据集是否与伯努利分布相一致,EstimatedDistribution 可用于通过给定数据估计伯努利参数分布,而 FindDistributionParameters 可用于将数据拟合为伯努利分布. ProbabilityPlot 可用于生成已知数据相对于符号式伯努利分布的 CDF 图形,而 QuantilePlot 可用于生成已知数据相对于符号式伯努利分布的分位数的分位数图形.
- TransformedDistribution 可用于表示伯努利分布的变换,TruncatedDistribution 可用于表示在上限和下限值之间截断值的分布. CopulaDistribution 可用于构建包含伯努利分布的更高维分布,而 ProductDistribution 可用于计算独立分量分布涉及伯努利分布的联合分布.
- BernoulliDistribution 与若干其他分布密切相关. 例如,BernoulliDistribution[p] 等价于 BinomialDistribution[1,p] 的一个单一实例,即 PDF[BernoulliDistribution[p],k] 等同于 Piecewise[Table[{PDF[BinomialDistribution[1,p],l],kl},{l,0,1}]]. 类似地,n 个独立且具有相同成功率 p 的伯努利变量的和可以通过 BinomialDistribution[n,p] 建模. 此外,从独立伯努利分布随机变量集合中自然产生的一些量值可以根据其它众所周知的分布进行建模. 例如,服从 BernoulliDistribution[p] 分布的前 n 个数据点的成功次数的分布为 BinomialDistribution[n,p],而获得一次成功所需的试验次数服从 GeometricDistribution[p] 分布,相应地,获取r 次成功则服从分布 NegativeBinomialDistribution[r,p].
范例
打开所有单元关闭所有单元范围 (8)
使用无量纲的 Quantity 来定义 BernoulliDistribution:
应用 (6)
在10个生产的灯泡中,1个是有缺陷的. 模拟100个灯泡的生产:
每种彩票每张1美元,共有10张. 每次只有一张获胜彩票. 一个赌徒有5美元用于购买彩票. 求如果他买的5张票都属于不同类型的彩票的话,他的获胜概率:
在一个光通信系统中,传输的光在接受端产生电流. 电子数服从泊松分布和其它分布的参数混合,并且取决于光类型. 如果光源使用强度为 ![]() 的相干激光,那么电子数分布是泊松分布:
的相干激光,那么电子数分布是泊松分布:
这是一个 PoissonDistribution:
如果光源使用热照明,那么泊松参数服从 ExponentialDistribution,其参数为 ![]() ,并且电子数目分布为:
,并且电子数目分布为:
属性和关系 (4)
可能存在的问题 (2)
文本
Wolfram Research (2007),BernoulliDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BernoulliDistribution.html (更新于 2016 年).
CMS
Wolfram 语言. 2007. "BernoulliDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/BernoulliDistribution.html.
APA
Wolfram 语言. (2007). BernoulliDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BernoulliDistribution.html 年
