BetaBinomialDistribution
BetaBinomialDistribution[α,β,n]
ベータ分布の母数が ![]() および
および ![]() で
で ![]() 回二項試行するベータ二項分布を表す.
回二項試行するベータ二項分布を表す.
詳細
- BetaBinomialDistributionはポリヤ(Pólya)分布や負の超幾何分布としても知られている.
- ベータ二項分布は,確率母数
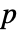 が形状母数 α および β のベータ分布に従う試行回数が n 回の二項分布である. »
が形状母数 α および β のベータ分布に従う試行回数が n 回の二項分布である. » - BetaBinomialDistributionでは,α および β は任意の正の実数でよく,n は任意の正の整数でよい.
- BetaBinomialDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- BetaBinomialDistribution[α,β,n]は,
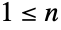 の整数値で定義される離散統計分布を表す.ただし,母数 α および β は形状母数として知られる正の実数であり,確率分密度関数(PDF)の全体的な形と動作を決定する.ベータ二項分布は離散PDFを持つことが多く,α および β の値によってPDFは単調増加,領域内に単一の「峰」または「谷」,あるいは一様な値を持つことがある.ベータ二項分布はPólya分布あるいは負の超幾何分布と呼ばれることがある.
の整数値で定義される離散統計分布を表す.ただし,母数 α および β は形状母数として知られる正の実数であり,確率分密度関数(PDF)の全体的な形と動作を決定する.ベータ二項分布は離散PDFを持つことが多く,α および β の値によってPDFは単調増加,領域内に単一の「峰」または「谷」,あるいは一様な値を持つことがある.ベータ二項分布はPólya分布あるいは負の超幾何分布と呼ばれることがある. - ベータ二項分布は,ベルヌーイ試行の既知の回数の成功確率 p がランダムで,関連する二項分布の成功確率 p がベータ分布(BetaDistribution)に従う,ベルヌーイ分布BernoulliDistribution)および二項分布(BinomialDistribution)の抽象化と考えることができる.ベイズの用語では,これはベータ二項分布が,成功確率 p についての事前分布がベータ分布である,二項変数の事後予測分布として発生したことを意味する.最初にドキュメントされたベータ二項分布の応用例は,1930年代のHugo Muenchによる臨床試験の確率的モデリングまで遡ることができる.今日でも,世界の現象の多くがベータ二項分布でモデル化できる.例えば,Pólyaの壷モデルの特別な抽出集合と置換規則にベータ二項分布を使うことができる.より最近では,ベータ二項分布は,生体認証デバイスのパフォーマンス評価,ベイズネットワークの研究,さまざまな人口知能アルゴリズム等に使われている.
- RandomVariateを使ってベータ二項分布から,1つあるいは複数の機械精度あるいは任意精度の(後者はWorkingPrecisionオプションを介して)擬似乱数変量を得ることができる.Distributed[x,BetaBinomialDistribution[α,β,n]](より簡略すると xBetaBinomialDistribution[α,β,n])を使って,確率変数 x が,ベルヌーイ分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[BetaBinomialDistribution[α,β,n],x]およびCDF[BetaBinomialDistribution[α,β,n],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.これらの数量はDiscretePlotを使って可視化することができる.
- DistributionFitTestを使って,与えられたデータ集合がベータ二項分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックベータ二項分布を推定することが,FindDistributionParametersを使ってデータをベータ二項分布にフィットすることができる.ProbabilityPlotを使って記号ベータ二項分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号ベータ二項分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたベータ二項分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってベータ二項分布を含む高次元分布を構築することが,ProductDistributionを使ってベータ二項分布を含む独立成分分布の結合分布を計算することができる.
- BetaBinomialDistributionは,他の多くの統計分布と関連がある.先述の通り,BetaBinomialDistributionは,BinomialDistributionとBetaDistributionの両方の特徴を組み合せており,この事実はParameterMixtureDistribution[BinomialDistribution[n,p],pBetaDistribution[α,β]]を評価するとBetaBinomialDistribution[α,β,n]になることを観察することで明白になる.同様に,DiscreteUniformDistribution[{0,n}]は厳密にBetaBinomialDistribution[1,1,n]と等しい.この事実から,UniformDistribution, TriangularDistribution,PERTDistributionとの定性的な繋がりが導かれる.BetaBinomialDistributionは,非常に自然なあり方でBetaNegativeBinomialDistributionと関係があり,MultinomialDistributionとDirichletDistributionがそれぞれBinomialDistributionとBetaDistributionのより高次のバージョンであるという事実から,BetaBinomialDistributionはいわゆるディリクレ多項式分布の1次元バージョンであると見ることができる.
例題
すべて開くすべて閉じるアプリケーション (4)
![]() についてベータ二項分布であると仮定し,100回試行して成功回数が50回より多くなる確率:
についてベータ二項分布であると仮定し,100回試行して成功回数が50回より多くなる確率:
黒いボールが ![]() 個,白いボールが
個,白いボールが ![]() 個入っている壷がある.
個入っている壷がある.![]()
![]() 番目の白いボールが壷から取り出される前に
番目の白いボールが壷から取り出される前に ![]() 個の黒いボールが置き換えなしにサンプルとして取られる確率を求める:
個の黒いボールが置き換えなしにサンプルとして取られる確率を求める:
あるいは,前述の ![]() 回の置き換えなしのサンプル抽出で
回の置き換えなしのサンプル抽出で ![]() 個の黒いボールがあったと仮定して白いボールを取り出す確率を計算する:
個の黒いボールがあったと仮定して白いボールを取り出す確率を計算する:
この分布は壷問題をモデル化する.壷には ![]() 個の白いボールと
個の白いボールと ![]() 個の黒いボールが入っている.壷からボールを取り出し,取り出したボールと同色の
個の黒いボールが入っている.壷からボールを取り出し,取り出したボールと同色の ![]() 個のボールと共に壷に戻す.この分布は
個のボールと共に壷に戻す.この分布は ![]() 回試行して
回試行して ![]() 個の白いボールを引き当てる確率を示している:
個の白いボールを引き当てる確率を示している:
特性と関係 (5)
負の整数,n より大きい整数,および整数ではない数を得る確率はゼロである:
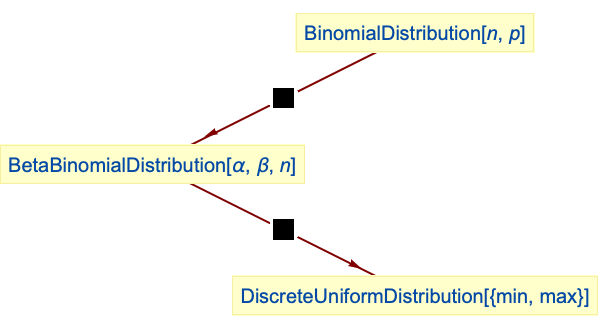
DiscreteUniformDistributionはベータ二項分布の特殊なケースである:
![]() で
で ![]() のときは,ベータ二項分布は三角形になるが,TriangularDistributionの離散ケースではない:
のときは,ベータ二項分布は三角形になるが,TriangularDistributionの離散ケースではない:
上記の式が,![]() がTriangularDistributionに従う場合の
がTriangularDistributionに従う場合の![]() の確率密度関数を与えることを確認する:
の確率密度関数を与えることを確認する:
BetaBinomialDistributionはBinomialDistributionとBetaDistributionを混合したものである:
考えられる問題 (3)
テキスト
Wolfram Research (2007), BetaBinomialDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/BetaBinomialDistribution.html.
CMS
Wolfram Language. 2007. "BetaBinomialDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BetaBinomialDistribution.html.
APA
Wolfram Language. (2007). BetaBinomialDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BetaBinomialDistribution.html