CauchyDistribution
CauchyDistribution[a,b]
位置母数 a,尺度母数 b のコーシー(Cauchy)分布を表す.
位置母数0,尺度母数1のコーシー分布を表す.
詳細
- CauchyDistributionは,Lorentz分布またはBreit–Wigner分布としても知られている.
- コーシー分布における値
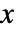 の確率密度は
の確率密度は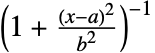 に比例する. »
に比例する. » - CauchyDistributionでは,a は任意の実数,b は任意の正の実数でよい.
- CauchyDistributionでは,a と b は単位次元が等しい任意の数量でよい. »
- CauchyDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- CauchyDistribution[a,b]は,実数集合上で定義され,2つの変数 a および b によってパラメータ化される連続統計分布を表す.ただし,a は実数値の「位置母数」であり,b は正の「尺度母数」である.コーシー分布の確率密度関数(PDF)は連続かつ単峰性であり,点
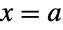 について対称である.PDFの高さと幅は,母数 b によって変わる.b の値が0に近付くと,より高くより急勾配のPDFになる.これに加え,PDFが
について対称である.PDFの高さと幅は,母数 b によって変わる.b の値が0に近付くと,より高くより急勾配のPDFになる.これに加え,PDFが 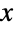 の大きい値について,指数的と言うよりも代数的に減少するという意味で,PDFの裾部は「厚い」.(この動作は,分布のSurvivalFunctionを分析することで,定量的に厳密にすることができる).コーシー分布は,ローレンツ分布あるいはBreit–Wigner分布と呼ばれることがある.
の大きい値について,指数的と言うよりも代数的に減少するという意味で,PDFの裾部は「厚い」.(この動作は,分布のSurvivalFunctionを分析することで,定量的に厳密にすることができる).コーシー分布は,ローレンツ分布あるいはBreit–Wigner分布と呼ばれることがある. - 現在コーシー分布と呼ばれているものの研究は,17世紀のフェルマの業績まで遡る.この分布は,分布の誕生からおよそ150年後の1850年代にオーギュスタン=ルイ・コーシーと関連付けられるまでに,すでに,既存の確率理論に豊かでカラフルな貢献をしていた.もともと,コーシー分布は,当時一般に受け入れられていた数多くの結果や概念に対する反例として作用する新しい分布として研究された.今日この分布は,それ自体として確立され,さまざまな分野における数多くの応用がある分布である.例えば,コーシー分布はある種の分子のブラウン運動と自然な結びつきを持ち,非相対的なコンテキストにおける共鳴のエネルギー断面を説明する分布である.コーシー分布は,また,危険分析,力学理論および電気理論,自然人類学を含む数多くの現象のモデル化に使うことができる.
- RandomVariateを使って,コーシー分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,CauchyDistribution[a,b]](より簡略すると xCauchyDistribution[a,b])を使って,確率変数 x がコーシー分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[CauchyDistribution[a,b],x]およびCDF[CauchyDistribution[a,b],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.コーシー分布の厚い裾部のために,ここに上げた数量の中には存在しないものがあるかもしれないので注意が必要である.
- DistributionFitTestを使って,与えられたデータ集合がコーシー分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからコーシーパラメトリック分布を推定することが,FindDistributionParametersを使ってデータをコーシー分布にフィットすることができる.ProbabilityPlotを使って記号的なコーシー分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号的なコーシー分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたコーシー分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってコーシー分布を含む高次元分布を構築することが,ProductDistributionを使ってコーシー分布を含む独立成分分布の結合分布を計算することができる.
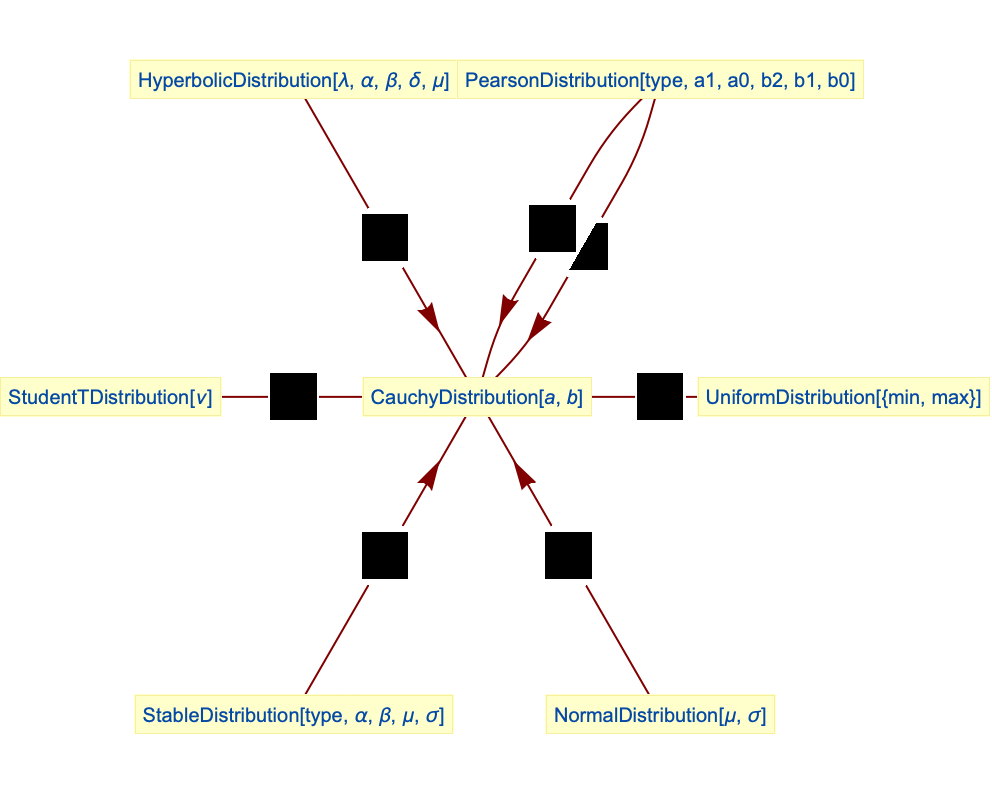
- コーシー分布は数多くの他の分布と関連している.例えば,CauchyDistribution[0,1]はStudentTDistribution[1]と厳密に等しいPDFを持つ.CauchyDistributonは,また,TransformedDistributionを介したNormalDistributionおよびUniformDistributionの両方の変換と見ることができ,ϵ が
 について0に近付くときのPearsonDistribution[4,1,-a,(1+ϵ)/2,-a,(a2+b2)/2]のPDFが,そして α が0に近付くときのHyperbolicDistribution[-1/2, α, 0, δ, μ]のPDFが,それぞれCauchyDistribution[a, b]およびCauchyDistribution[μ, δ]のPDFと厳密に等しいという意味において,PearsonDistributionおよびHyperbolicDistributionの両方にとっての極限のケースである.CauchyDistributionは,PearsonDistribution,ParetoDistribution,StableDistributionとも関係がある.
について0に近付くときのPearsonDistribution[4,1,-a,(1+ϵ)/2,-a,(a2+b2)/2]のPDFが,そして α が0に近付くときのHyperbolicDistribution[-1/2, α, 0, δ, μ]のPDFが,それぞれCauchyDistribution[a, b]およびCauchyDistribution[μ, δ]のPDFと厳密に等しいという意味において,PearsonDistributionおよびHyperbolicDistributionの両方にとっての極限のケースである.CauchyDistributionは,PearsonDistribution,ParetoDistribution,StableDistributionとも関係がある.
例題
すべて開くすべて閉じるスコープ (6)
サンプルの密度ヒストグラムを推定された分布の確率密度関数と比較する:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (1)
振子が原点の上,高さ ![]() のところに掛っている.この振子と垂直軸によってできる角
のところに掛っている.この振子と垂直軸によってできる角 ![]() は
は![]() から
から ![]() までで一様分布に従う.振子と垂直軸の間の水平距離
までで一様分布に従う.振子と垂直軸の間の水平距離 ![]() を求める[MathWorld]:
を求める[MathWorld]:
以下で示されるように,これはCauchyDistributionである:
特性と関係 (13)
コーシー分布は平行移動と正の因子によるスケーリングの下では閉じている:
0を中心としたコーシー分布の逆分布もまたコーシー分布である:
CauchyDistribution[0,1]は,![]() のStudentTDistributionに等しい:
のStudentTDistributionに等しい:
正規分布に従う2つの変数の比はCauchyDistributionである:
![]() が一様分布に従う場合,
が一様分布に従う場合,![]() はCauchyDistributionを示す:
はCauchyDistributionを示す:
コーシー分布はタイプ4のピアソン分布(PearsonDistribution)の限定されたケースである:
CauchyDistributionはタイプ7のPearsonDistributionの特殊ケースである:
コーシー分布はStableDistributionである:
CauchyDistributionは,![]() かつ
かつ ![]() とすると,
とすると,![]() のときのHyperbolicDistributionの特異極限である:
のときのHyperbolicDistributionの特異極限である:
CauchyDistributionのLogLikelihood関数は複数の極大値を持つことがある:
考えられる問題 (2)
テキスト
Wolfram Research (2007), CauchyDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/CauchyDistribution.html (2016年に更新).
CMS
Wolfram Language. 2007. "CauchyDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/CauchyDistribution.html.
APA
Wolfram Language. (2007). CauchyDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CauchyDistribution.html