Search for all pages containing CellularAutomaton
CellularAutomaton[rule,init,t]
generates a list representing the evolution of the cellular automaton with the specified rule from initial condition init for t steps.
CellularAutomaton[rule,init]
gives the result of evolving init for one step.
CellularAutomaton[rule,init,{tspec,xspec,…}]
gives only those parts of the evolution specified by tspec, xspec, etc.
CellularAutomaton[rule,init,{t,All,…}]
includes at each step all cells that could be affected over the course of t steps.
CellularAutomaton[rule]
is an operator form of CellularAutomaton that represents one step of evolution.




CellularAutomaton
CellularAutomaton[rule,init,t]
generates a list representing the evolution of the cellular automaton with the specified rule from initial condition init for t steps.
CellularAutomaton[rule,init]
gives the result of evolving init for one step.
CellularAutomaton[rule,init,{tspec,xspec,…}]
gives only those parts of the evolution specified by tspec, xspec, etc.
CellularAutomaton[rule,init,{t,All,…}]
includes at each step all cells that could be affected over the course of t steps.
CellularAutomaton[rule]
is an operator form of CellularAutomaton that represents one step of evolution.
Details








- Possible forms for rule are:
-
n 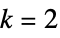 ,
, 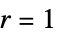 , elementary rule with rule number n
, elementary rule with rule number n{n,k} general nearest‐neighbor rule with k colors {n,k,r} general rule with k colors and range r {n,k,{r1,r2,…,rd}} d‐dimensional rule with 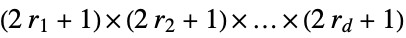 neighborhood
neighborhood {n,k,{{off1},{off2},…,{offs}}} rule with neighbors at specified offsets {n,k,rspec,s} order‐s rule {n,{k,1}} k‐color nearest‐neighbor totalistic rule {n,{k,1},r} k‐color range-r totalistic rule {n,{k,{wt1,wt2,…}},rspec} rule in which neighbor i is assigned weight wti {lhs1->rhs1,lhs2->rhs2,…} explicit replacements for lists of neighbors {fun,{},rspec} general function fun to apply to each list of neighbors bfun Boolean function to apply to collections of neighbors CellularAutomaton[rule] operator form of a rule <|"key1"val1,"key2"val2,…|> rule specification by an association "name" named rule - CellularAutomaton[{n,k},…] is equivalent to CellularAutomaton[{n,{k,{k^2,k,1}}},…].
- The following keys can be used to specify a rule given as an association:
-
"RuleNumber" n rule number "TotalisticCode" n totalistic code "OuterTotalisticCode" n outer totalistic code "GrowthCases" {g1,g2,…} make a cell 1 when gi of its neighbors are 1 "GrowthSurvivalCases" {{g1,…},{s1,…}} 1 for gi neighbors; unchanged for si "GrowthDecayCases" {{g1,…},{d1,…}} 1 for gi neighbors; 0 for di "Dimension" d overall dimension "Colors" k number of colors "Range" r range of rule "Neighborhood" type neighborhood type - With "GrowthCases"->{g1,g2,…}, a cell goes from value 0 to value 1 if it has gi neighbors that are 1; otherwise it stays the same as before.
- With "GrowthSurvivalCases"->{{g1,…},{s1,…}}, a cell goes from value 0 to value 1 if it has gi neighbors that are 1, maintains value 1 if it has si neighbors that are 1, and otherwise gets value 0.
- With "GrowthDecayCases"->{{g1,…},{d1,…}}, a cell goes from value 0 to value 1 if it has gi neighbors that are 1, gets value 0 if it has di neighbors that are 1, and otherwise stays the same.
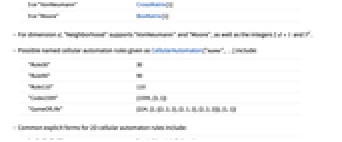
- Possible settings for "Neighborhood" in 2D include:
-
5 or "VonNeumann" CrossMatrix[1] 9 or "Moore" BoxMatrix[1] - For dimension d, "Neighborhood" supports "VonNeumann" and "Moore", as well as the integers
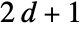 and
and 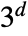 .
. - Possible named cellular automaton rules given as CellularAutomaton["name",…] include:
-
"Rule30" 30 "Rule90" 90 "Rule110" 110 "Code1599" {1599,{3,1}} "GameOfLife" {224,{2,{{2,2,2},{2,1,2},{2,2,2}}},{1,1}} - Common explicit forms for 2D cellular automaton rules include:
-
{n,{k,1},{1,1}} 9‐neighbor totalistic rule {n,{k,{{0,1,0},{1,1,1},{0,1,0}}},{1,1}} 5‐neighbor totalistic rule {n,{k,{{0,k,0},{k,1,k},{0,k,0}}},{1,1}} 5‐neighbor outer totalistic rule - The number of possible cellular automaton rules is as follows:
-
elementary rules 256 1D general rules 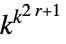
1D totalistic rules 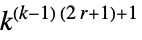
2D general rules 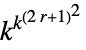
2D 9‐neighbor totalistic rules 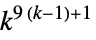
2D 5‐neighbor totalistic rules 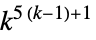
2D 5‐neighbor outer totalistic rules 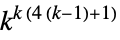
- Normally, all elements in init and the evolution list are integers between 0 and
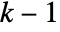 .
. - When a general function or a replacement list is used, the elements of init and the evolution list can be any expressions. »
- Explicit replacement rules lhsi->rhsi can contain patterns.
- In a 1D cellular automaton, replacement rules or an explicit function fun are always taken to apply to a 1D list of neighbors. If the neighbors are specified by explicit offsets, they are given in the order of the offsets.
- When the neighborhood in a multidimensional cellular automaton is defined by a range specification such as {r1,r2,…}, the list of neighbors is taken to be a full array with dimensions 2{r1,r2,…}+1.
- If the neighbors in a multidimensional cellular automaton are specified by an explicit list of offsets, the neighbors are supplied in a one-dimensional list in the order of the offsets.
- If an explicit function fun is given, the first argument supplied to it is the list of neighbors. The second argument is the step number starting at 0.
- A complete rule specification is considered to be a pure Boolean function bfun if BooleanVariables[bfun] yields an integer v. In this case, bfun is applied to neighborhoods of v cells at each step. The neighborhoods extend Ceiling[v/2] cells to the left.
- In an order‐s cellular automaton, specified by {rule,kspec,rspec,s}, each step depends on s preceding steps.
- Initial conditions are constructed from init as follows:
-
{a1,a2,…} explicit list of values ai, assumed cyclic {{a1,a2,…},b} values ai superimposed on a b background {{a1,a2,…},{b1,b2,…}} values ai superimposed on a background of repetitions of b1, b2, … {{{{a11,a12,…},off1}, {{a21,…},off2},…},bspec} values aij at offsets offi on a background {{a11,a12,…},{a21,…},…} explicit list of values in two dimensions {aspec,bspec} values in d dimensions with d‐dimensional padding - The first element of aspec is superimposed on the background at the first position in the positive direction in each coordinate relative to the origin. This means that bspec[[1,1,…]] is aligned with aspec[[1,1,…]].
- CellularAutomaton[rule,init,t] generates an evolution list of length
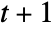 .
. - For an order‐s cellular automaton, init is a list giving the initial s steps in the evolution of the system.
- Time specifications tspec in {tspec,xspec,…} can be as follows:
-
t all steps 0 through t {t} a list containing only step t {{t}} step t alone {t1,t2} steps t1 through t2 {t1,t2,dt} steps t1, t1+dt, … - The initial condition is considered to be at step 0.
- CellularAutomaton[rule,init,{tspec}] uses the default Automatic for xspec.
- Space specifications xspec can be as follows:
-
All all cells that can be affected by the specified initial condition Automatic all cells in the region that differs from the background 0 cell aligned with beginning of aspec x cells at offsets up to x on the right -x cells at offsets up to x on the left {x} cell at offset x to the right {-x} cell at offset x to the left {x1,x2} cells at offsets x1 through x2 {x1,x2,dx} cells x1, x1+dx, … - In one dimension, the first element of aspec is taken by default to have space offset 0.
- In any number of dimensions, aspec[[1,1,1,…]] is taken by default to have space offset {0,0,0,…}.
- Each element of the evolution list produced by CellularAutomaton is always the same size.
- With an initial condition specified by an aspec of width
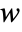 , the region that can be affected after
, the region that can be affected after 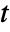 steps by a cellular automaton with a rule of range
steps by a cellular automaton with a rule of range 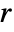 has width
has width 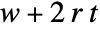 .
. - If no bspec background is specified, space offsets of All and Automatic will include every cell in aspec.
- A space offset of All includes all cells that can be affected by the initial condition.
- A space offset of Automatic can be used to trim off background from the sides of a cellular automaton pattern.
- In working out how wide a region to keep, Automatic only looks at results on steps specified by offt.
- CellularAutomaton[rule][init] is equivalent to CellularAutomaton[rule,init].
Examples
open all close allBasic Examples (3)
Scope (91)
One-Dimensional Rules (26)
Generate the same result using RulePlot:
3-color totalistic rule with code 867:
2-color range-![]() (two neighbors on the left and one on the right) rule 23898:
(two neighbors on the left and one on the right) rule 23898:
Rule 30 specified by giving explicit offsets for cells in its neighborhood:
An analog of rule 30 with modified offsets:
Rule 30 specified by giving explicit weights for cells in its neighborhood:
Totalistic rules have weight 1 for each offset in the neighborhood:
A 3-color outer totalistic rule:
Specify rule 90 by giving explicit replacements for neighborhoods:
Specify rule 90 by giving a single "algebraic" replacement rule:
Use an explicit Boolean formula for rule 30, operating on True and False states:
Values in a cellular automaton can be any symbolic expression:
Use an arbitrary symbolic function f as the rule to apply to range-1 neighbors:
Apply the function to neighbors with offsets ![]() and
and ![]() :
:
Set up a "Pascal's triangle cellular automaton":
Specify rule 90 as an explicit function:
Additive cellular automaton modulo 4:
The second argument to the function is the step number:
Change the rule at successive steps; #2 gives the step number:
Use continuous values for cells:
Specify rule 90 as a pure Boolean function:
An ![]() analog of rule 90 specified using a pure Boolean function:
analog of rule 90 specified using a pure Boolean function:
Rules Specified by Associations (5)
Initial Conditions (8)
Explicit initial conditions are assumed cyclic:
The left neighbor of the leftmost cell is the rightmost cell, and vice versa:
Start with a "seed" consisting of the block 11101 surrounded by 0s:
Start from a single 0 surrounded by 1s:
Start from 111 on a background of repeated 10 blocks:
Specify the "seed" as a sparse array:
Use a SparseArray to give the complete cyclic initial condition:
Time Steps (6)
Region Specifications (11)
By default, CellularAutomaton automatically cuts off the region not covered by the pattern:
Include all cells that could possibly be affected given the structure of the rule:
Include only the region that differs from the background:
Include all cells that could possibly be affected:
By default, different rules give regions of different widths:
Force all rules of the same type to give regions of the same width:
The region that can possibly be affected depends on the range of the rule:
Show only the region from cell 0 (the position of the initial 1) to cell 40:
Negative positions are on the left:
Give the region consisting just of cell 0 at each step:
Include only the value of cell 0, not in a list:
Show every other cell in time and space:
Cell 0 is always the leftmost cell in the explicit part of the initial condition:
Repeat a finite block to fill the region of initial conditions from positions ![]() to
to ![]() :
:
Multidimensional Rules (13)
Evolve range-1 2D (9-neighbor) totalistic code 14 for 2 steps:
Give only the result after 2 steps:
Show the result after 30 steps:
Show the mean color of each cell:
Show the space-time history as a 3D image:
Show a cube at the position of each 1 cell:
A spacetime slice for 50 steps across all ![]() values at
values at ![]() offset 0:
offset 0:
Mean colors of all cells with particular ![]() positions:
positions:
Use RulePlot to visualize the totalistic rule specification:
5-neighbor outer totalistic rule:
Use RulePlot to visualize the outer totalistic rule specification:
Use an initial condition with two black cells, specified in a sparse array:
Multidimensional Rules Specified by Associations (8)
Specify 2D totalistic code 14 using an association (with a 9-cell neighborhood assumed):
5-neighbor totalistic code 26:
Describe the neighborhood using the string "VonNeumann":
5-neighbor outer totalistic code 110:
Growth rule in which cells get value 1 when they have 1 or 2 neighbors (of 9) with value 1:
Growth-decay rule in which cells get value 1 when they have 1 or 2 neighbors with value 1, and get value 0 if they have 6 or 7 neighbors with value 1:
Rule in which cells get value 1 when they have 1 or 2 neighbors with value 1, keep their value if they have 6 or 7 neighbors with value 1, and get value 0 otherwise:
Rule in which cells get value 1 when they have 1 neighbor (of 7) with value 1:
Rule in which cells get value 1 when they have 1 neighbor (of 27) with value 1:
Higher-Order Rules (6)
Rule 30 written out explicitly as a "first-order rule":
A second-order analog of rule 30, involving two steps of initial conditions:
Include both initial-condition steps in the output:
Second-order rule 1008, starting with a single 1 in both initial condition steps:
Include both steps in the initial conditions:
Second-order totalistic rule 10 with 2 colors and range 1:
A ![]() -order version of the same rule:
-order version of the same rule:
Rule 150R—the second-order reversible mod 2 rule:
A spacetime slice of a second-order totalistic rule with 2 colors and range 1:
Applications (23)
Make a color picture of rule 30:
Make pictures of the first 32 elementary cellular automata:
Show the 2-color range-2 totalistic code 20 cellular automaton from a sequence of initial conditions:
Show results for 3-color range-3 totalistic code 1599 for different initial conditions:
Pad with three 0s at the side of each pattern:
Show a single evolution in multiple "panels":
Make a "random" walk from the values of cells on the center column of rule 30:
Find repetition periods of rule 90 in cyclic regions of successive widths:
Draw the state transition graph for rule 110 in a region of size 7:
Generate a difference pattern for two cellular automata with initial conditions differing by one bit:
Show the common evolution in gray:
Use an outer-totalistic 2D cellular automaton to generate a maze-like pattern:
Use a growth rule to generate an irregular pattern:
Show steps in the evolution of a 5-neighbor outer-totalistic 2D cellular automaton:
Show a "glider" in the Game of Life:
Show the evolution of the "puffer train" in the Game of Life:
The Game of Life from random initial conditions, averaged for 100 steps:
Patterns generated by a sequence of 2D 9-neighbor rules:
Render a 3D view of a 2D cellular automaton evolution using spheres:
Show a sequence of steps in the evolution of a 3D cellular automaton:
Show time averages of slices at a sequence of heights in a 3D cellular automaton:
A cellular automaton based on multiplication of complex integers:
Properties & Relations (9)
Highlight the center column of cells:
Use RulePlot to generate graphics:
Image generates an image in which each cell is a single pixel:
![]() steps of cellular automaton evolution give a list of length
steps of cellular automaton evolution give a list of length ![]() :
:
Initial conditions given as explicit lists are assumed cyclic:
The center cell starting from all possible tuples gives the digits in the rule number:
Here is a 5-neighbor outer totalistic code:
Generate its RulePlot:
Possible Issues (7)
By default, the lists in each evolution are made only as long as they need to be:
Use {t,All} to get lists of the same length for all rules of a particular type:
If no cells ever differ from the background, the automatically selected region will always be empty:
Rules with alternating backgrounds can give lists which contain only 0s:
If the evolution is continued for 2 steps, explicit 1s are included in the 1-step result:
In this form, a specification of the background is included:
By default, each evolution is made only as wide as it needs to be:
Use {t,All} to get consistent widths:
A 3-color rule may generate only values 0 and 1:
If visualized with ArrayPlot, the value 1 will be shown black:
Use RulePlot to show colors correctly based on the underlying rule:
Explicit ColorRules also avoids the problem with default ArrayPlot:
Use RulePlot to show the underlying rule:
Cells and steps in CellularAutomaton are not numbered according to their part numbers:
Rule numbers have different meanings when the offsets are specified in different orders:
See Also
ListConvolve ArrayFilter BlockMap Partition BooleanFunction BooleanTable BitXor BitShiftLeft RulePlot ArrayPlot CenterArray ShiftRegisterSequence TuringMachine SubstitutionSystem
Function Repository: SequentialCellularAutomaton BlockCellularAutomaton ProbabilisticCellularAutomaton ReversibleCellularAutomaton DynamicCellularAutomaton MobileAutomaton AggregationSystem IteratedFiniteAutomaton CellularAutomatonFromNumber CellularAutomatonNumber
History
Introduced in 2002 (4.2) | Updated in 2007 (6.0) ▪ 2008 (7.0) ▪ 2016 (10.4) ▪ 2016 (11.0) ▪ 2017 (11.1)
Text
Wolfram Research (2002), CellularAutomaton, Wolfram Language function, https://reference.wolfram.com/language/ref/CellularAutomaton.html (updated 2017).
CMS
Wolfram Language. 2002. "CellularAutomaton." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/CellularAutomaton.html.
APA
Wolfram Language. (2002). CellularAutomaton. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CellularAutomaton.html
BibTeX
@misc{reference.wolfram_2025_cellularautomaton, author="Wolfram Research", title="{CellularAutomaton}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/CellularAutomaton.html}", note=[Accessed: 19-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_cellularautomaton, organization={Wolfram Research}, title={CellularAutomaton}, year={2017}, url={https://reference.wolfram.com/language/ref/CellularAutomaton.html}, note=[Accessed: 19-December-2025]}