CensoredDistribution

CensoredDistribution[{xmin,xmax},dist]

表示的分布值来自于 dist，并且被删截为位于 xmin 和 xmax 之间.

CensoredDistribution[{{xmin,xmax},{ymin,ymax},…},dist]

表示的分布值来自于多变量分布 dist，并且被删截为位于 xmin 和 xmax、ymin 和 ymax 等之间.

更多信息

背景

  • CensoredDistribution[{xmin,xmax},dist] 表示一个从区间 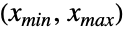内所有 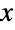的单变量分布中提取的对数据建模的统计分布，并且对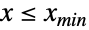于 总等于 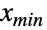（相应的，对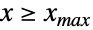于 总等于 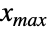）. 术语未删截、左删截、右删截和双删截分别描述 {xmin,xmax} 是 {-∞,∞}、{xmin,∞}、{-∞,xmax} 和 {xmin,xmax} 形式的单变量删截，其中单变量 dist 可以是连续的（如 NormalDistribution、 GammaDistribution 或 BetaDistribution）或离散的（如 PoissonDistribution、 BinomialDistribution 或 BernoulliDistribution）并可以（分别通过 TransformedDistribution、 CensoredDistribution 和 TruncatedDistribution）作为已知分布的变形、删截或截断定义.
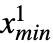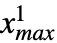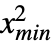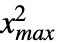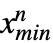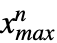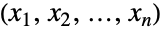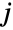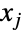  • 类似地，多变量的 CensoredDistribution[{{,},{,},… ,{,}},dist] 表示从多变量分布 dist 中提取的向量 的分布，其中第 个成分 位于区间 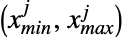中. 正如单变量的情况，多变量 dist 可以使连续的（如 MultinormalDistribution）或离散的（ MultivariateHypergeometricDistribution），也可以（分别通过 CopulaDistribution 和 ProductDistribution）作为一只分布的耦合或乘积定义.
  • 当对只知道部分数值的数据（即那些只含有部分观测或精度受限的数据的数据集）进行建模时可用删截分布，而对含有删截值的数据集的分析可以追溯到18世纪 Daniel Bernoulli 对天花的研究. 这样的数据在医药和心理学等领域中是比较普遍的，在不时需要未发现世纪故障时做出失效预测的可靠性和制造业中也相对普遍. 删截分布也是生存分析中的常用工具，以及为分析这样的数据集而存在的各种专业统计工具（如删失回归）.
  • 根据定义， CensoredDistribution[{xmin,xmax},dist] 等价于 TransformedDistribution[f,xdist]，其中 f 由 Piecewise[{{xmin,x<=xmin},{x,xmin<x<xmax},{xmax,x>=xmax}}] 给出. CensoredDistribution 常与 TruncatedDistribution 混淆，但这两者有本质上的区别，删截将概率置于删截区间最后，而截尾将概率分布在截尾区间上.

范例

打开所有单元关闭所有单元

基本范例  (2)

定义一个左删截离散分布：

概率密度函数：

定义一个右删截连续分布：

累积分布函数：

范围  (26)

基本用途  (9)

为一元离散分布定义不同的删截类型：

为一元连续分布定义不同的删截类型：

定义一个右删截离散分布：

比较概率密度函数：

求删截分布在9处的概率：

与原分布得到不小于9的值的概率比较：

对一个连续分布进行删截：

使用直方图并绘制原密度函数，以得到点概率的视图：

在一点处删截的分布：

一个多元连续分布的删截：

计算该分布的一个表达式的期望：

一个多元离散分布的删截：

计算分布的均值：

与从分布中随机抽样得到的结果进行比较：

定义一个双删截分布：

累积分布函数：

删截分布的均值与方差：

Moment 具有符号式阶数的解析式：

估计删截区间：

参数分布  (5)

定义一个右删截连续分布：

累积分布函数：

绘制随机样本的直方图. 尖峰对应于 PDF 的 DiracDelta 部分：

定义一个删截的 GeometricDistribution：

比较概率密度函数：

在删截点处的概率密度函数值等于下面的概率：

定义一个双删截 GammaDistribution：

求母函数：

定义一个右删截 PoissonDistribution：

比较 HazardFunction：

定义一个二维删截 DirichletDistribution：

比较累积分布函数：

删截分布的均值与方差：

计算概率与期望：

非参数分布  (3)

定义一个删截的 EmpiricalDistribution：

比较累积分布函数：

定义一个删截的 HistogramDistribution：

比较累积分布函数：

定义一个删截的 SmoothKernelDistribution：

比较累积分布函数：

导出分布  (9)

定义一个删截 ParameterMixtureDistribution：

累积分布函数：

定义一个删截 MixtureDistribution：

累积分布函数：

定义一个删截 OrderDistribution：

概率密度函数：

比较均值：

定义一个删截 CensoredDistribution：

概率密度函数：

与双删截泊松分布比较：

定义一个删截 TruncatedDistribution：

比较累积分布函数：

定义一个删截 TransformedDistribution：

累积分布函数：

定义一个删截 MarginalDistribution：

概率密度函数：

与边缘分布的概率密度函数比较：

定义一个删截 ProductDistribution：

利用随机样本制作密度函数的视图：

QuantityDistribution 的删截估值为 QuantityDistribution：

计算平均速度：

应用  (4)

一家保险公司在留用水平 处购买再保险. 假定索赔服从对数正态分布，求保险公司支付额随机变量的矩：

求再保险公司支付随机变量的矩：

一个组件的生命期服从 RayleighDistribution. 使用 小时时间，对组件进行检测，如果在这段时间内组件没有失效，那么假定这个组件的生命期恰好是 小时. 求满足至少有 5% 的被检测组件的生命期长于 的条件下，检测的时间长度：

对于 ，求检测的生命期分布：

比较删截分布与实际生命期分布：

比较平均生命期：

一名高尔夫初学者要使球进入一个四杆洞所需的击球次数服从均值为 8 的一个 PoissonDistribution 分布. 假定在这个高尔夫球场上，在第10次击球后，这名选手就把球捡起来，求在一个四杆洞中球入洞次数的分布：

概率密度函数：

在高尔夫球场内，一个4杆洞所需的平均击球次数：

求要使球入洞，这名选手需要的击球次数超过4次的概率：

美国成年男性的体重服从均值为 191 磅、标准差为 70 磅的正态分布. 假定每个浴室磅秤的上限为 300 磅，求当使用普通浴室磅秤测量时得到的体重分布：

累积分布函数：

利用一个随机样本，将密度函数可视化表示：

求平均体重：

求体重至少为 200 磅的概率：

求体重恰好位于磅秤上限或者高于这个上限的概率：

与未删截分布进行比较：

属性和关系  (4)

CensoredDistribution 是 TransformedDistribution 的一种特殊情况：

对于一个离散分布，比较删截与截断：

在删截的情况下，来自外部的权值位于删截区间的两端：

在截断的情况下，来自外部的权重在截断区间中均匀分布：

对于一个连续分布，比较删截与截断：

在删截的情况下，概率位于删截区间的一端：

在截断的情况下，概率分布在截断区间上：

一个连续分布的删截可能会导致一个既不连续又不离散的混合分布：

该混合型删截分布的 CDF 在删截点不连续：

可视化该累积分布函数：

删截分布的概率密度函数没有定义， PDF 返回未估值：

CDF 的微分结果是一个不能积分成 1 的函数：

概率密度估计函数样本在样本量增大时不收敛：

将其与潜在连续分布的直方图比较，估计函数收敛：

可能存在的问题  (1)

连续分布的删截可能导致一个既不连续又不离散的混合分布：

该混合型删截分布的 PDF 无定义： »

完全支持混合型分布的计算. 计算特殊矩：

估计一个删截分布：

混合型分布可以理解为连续分布和离散分部的混合：

Wolfram Research (2010)，CensoredDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CensoredDistribution.html （更新于 2016 年）.

文本

Wolfram Research (2010)，CensoredDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CensoredDistribution.html （更新于 2016 年）.

CMS

Wolfram 语言. 2010. "CensoredDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/CensoredDistribution.html.

APA

Wolfram 语言. (2010). CensoredDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CensoredDistribution.html 年

BibTeX

@misc{reference.wolfram_2024_censoreddistribution, author="Wolfram Research", title="{CensoredDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/CensoredDistribution.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_censoreddistribution, organization={Wolfram Research}, title={CensoredDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/CensoredDistribution.html}, note=[Accessed: 14-November-2024 ]}