ComplexPlot
ComplexPlot[f,{z,zmin,zmax}]
在边角为 zmin 和 zmax 的复矩形内绘制 Arg[f].
更多信息和选项




- ComplexPlot 对 Arg[f] 使用循环颜色函数来标识特征点,如零点、极点和本质奇点. 颜色函数在零点周围逆时针从
 到
到  ,在极点周围为顺时针,在本质奇点附近为无穷多个环.
,在极点周围为顺时针,在本质奇点附近为无穷多个环. - ComplexPlot[pred,{z,n}] 等价于 ComplexPlot[pred,{z,-n-n I,n+n I}].
- ComplexPlot 将变量 z 视为局部变量,相当于使用 Block.
- ComplexPlot 具有属性 HoldAll,并且仅在对 z 赋特定的数值后才对 f 求值. 在某些情况下,先使用 Evaluate 符号式运算 f 可能会更有效.
- 在 f 的计算结果为 None 的区域不应用任何颜色.
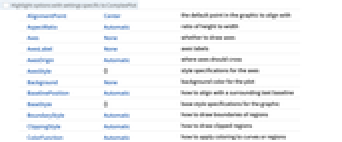
- ComplexPlot 和 Graphics 有相同的选项,不同之处和更多选项如下所示: [所有选项的列表]
-
Axes None 是否绘制坐标轴 BoundaryStyle Automatic 怎样绘制区域的边界 ClippingStyle Automatic 怎样绘制剪切掉的区域 ColorFunction Automatic 怎样为曲线或区域着色 ColorFunctionScaling True 是否对 ColorFunction 的参数进行缩放 EvaluationMonitor None 每次运行函数时要计算的表达式 Exclusions Automatic 要排除在外的 x、y 曲线 ExclusionsStyle None 在要排除在外的点或曲线处绘制什么 Frame Automatic 是否为图形绘制边框 MaxRecursion Automatic 递归子划分的最大数量 Mesh None 绘制多少个网格 MeshFunctions Automatic 如何确定网格的放置 MeshShading None 怎样处理网格点或线之间区域的色调 MeshStyle Automatic 网格的样式 PlotLegends None 颜色梯度的图例 PlotPoints Automatic 每个方向上初始采样点的个数 PlotRange Automatic 包含的值的范围 PlotRangeClipping True 在绘图范围边界处是否进行剪切 RegionFunction (True&) 怎样确定是否要包含某个点 WorkingPrecision MachinePrecision 内部计算使用的精度 PerformanceGoal $PerformanceGoal 优化的目标 PlotTheme $PlotTheme 绘图的整体外观主题 - ColorFunction->{cfunc,sfunc} 用 cfunc 生成基础颜色,用 sfunc 调整颜色以突出显示特征.
- sfunc 的可能的已命名设置有:
-

Automatic 根据 Abs[f] 自动调整明暗 
"MaxAbs" Abs[f] 较大值的浅色调 
"LocalMaxAbs" Abs[f] 的上四分位数的的浅色调 
"GlobalAbs" 与 Abs[f] 从小到大的值对应的由暗到亮的色调 
"QuantileAbs" 基于 Abs[f] 的分位数的由暗到亮的色调 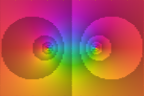
"CyclicLogAbs" Log[Abs[f]] 的循环的由暗到亮的色调 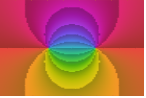
"CyclicArg" Arg[f] 的循环的由暗到亮的色调 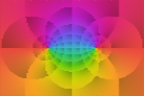
"CyclicLogAbsArg" Log[Abs[f]] 和 Arg[f] 的循环的色调 
"CyclicReImLogAbs" Re[f] 和 Im[f] 的暗色环,Log[Abs[f]] 的浅色环 
"ShiftedCyclicLogAbs" 超过特定阈值后的 Log[Abs[f]] 的循环的色调 
None 不改变色调 - 为 MeshFunctions 和 RegionFunction 中的函数提供的参数为
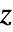 、
、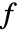 . 默认情况下,为 ColorFunction 中的函数提供的是 Re[z]、Im[z]、Abs[z]、Arg[z]、Re[f]、Im[f]、Abs[f]、Arg[f] 经过缩放的版本.
. 默认情况下,为 ColorFunction 中的函数提供的是 Re[z]、Im[z]、Abs[z]、Arg[z]、Re[f]、Im[f]、Abs[f]、Arg[f] 经过缩放的版本.

所有选项的列表



范例
打开所有单元关闭所有单元范围 (23)
采样 (9)
演示 (14)
用 "CyclicLogAbs" 循环调整色调以给出 Abs[f] 的等值线:
用 "CyclicArg" 循环调整色调以给出 Arg[f] 的等值线:
用 "CyclicLogAbsArg" 循环调整色调以给出 Abs[f] 和 Arg[f] 的等值线:
用 "GlobalAbs" 突出显示零点(黑色)和极点(白色):
用 "QuantileAbs" 加深 Abs[f] 较小值的色调,使 Abs[f] 较大值的色调更明亮:
用 "MaxAbs" 使 Abs[f] 较大值的色调更明亮:
用 "LocalMaxAbs" 使 Abs[f] 相对较大的值的色调更明亮:
用 "CyclicReImLogAbs" 根据 Re[f] 和 Im[f] 循环加深色调,根据 Log[Abs[f]] 循环调亮色调:
选项 (48)
AspectRatio (4)
ColorFunction (14)
LogGamma 和 Log[Gamma] 有不同的分支切割:
指定自定义 ColorFunction:
颜色函数取决于八个参数 (Re[z]、Im[z]、Abs[z]、Arg[z]、Re[f]、Im[f]、Abs[f]、Arg[f]):
可调整颜色函数的色调以突出显示图形的特征,如零点、极点和鞍点. 用 "CyclicLogAbs" 循环调整色调给出 Abs[f] 在 2 的幂处的等值线:
用 "CyclicArg" 循环调整色调给出 Arg[f] 的在 ![]() /6 整数倍处的等值线:
/6 整数倍处的等值线:
用 "CyclicLogAbsArg" 调色函数组合 "CyclicLogAbs" 和 "CyclicArg" 的效果:
可调整任意 ColorFunction 的色调:
用 "GlobalAbs" 突出显示零点(黑色)和极点(白色):
用 "QuantileAbs" 使图像上 Abs[f] 相对较大值处的色调更明亮:
用 "MaxAbs" 使图像上 Abs[f] 较大值处的色调更明亮:
用 "LocalMaxAbs" 使图像上 Abs[f] 相对较大值处的色调更明亮:
用 "ShiftedCyclicLogAbs" 根据 Log[Abs[f]] 在零点周围生成色轮及循环色调:
用 "CyclicReImLogAbs" 根据 Re[f] 和 Im[f] 循环加深绘图的色调,根据 Log[Abs[f]] 循环调亮绘图的色调:
ColorFunctionScaling (1)
Exclusions (4)
MaxRecursion (1)
如果使用了区域函数,MaxRecursion 会调整初始网格:
MeshFunctions (2)
PlotLegends (2)
RegionFunction (3)
应用 (28)
属性和关系 (8)
ComplexPlot 是 DensityPlot 的特殊情形:
使用 ComplexPlot3D 用 ![]() 轴作为幅值:
轴作为幅值:
用 ComplexArrayPlot 绘制复数数组:
外观可能与 ComplexPlot 的结果不一样,取决于数据的组合方式:
使用 ReImPlot 和 AbsArgPlot 在实数上绘制复数值:
使用 ComplexListPlot 显示复数在平面中的位置:
ComplexContourPlot 在复平面上绘制曲线:
ComplexRegionPlot 在复平面上绘制区域:
ComplexStreamPlot 和 ComplexVectorPlot 将复数视为方向:
可能存在的问题 (2)
文本
Wolfram Research (2019),ComplexPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ComplexPlot.html (更新于 2021 年).
CMS
Wolfram 语言. 2019. "ComplexPlot." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/ref/ComplexPlot.html.
APA
Wolfram 语言. (2019). ComplexPlot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ComplexPlot.html 年