CompoundPoissonDistribution
CompoundPoissonDistribution[λ,dist]
比率の母数が λ でジャンプサイズ分布 dist の複合ポアソン(Poisson)分布を表す.
詳細
- CompoundPoissonDistributionは中断和分布としても知られている.
- 複合ポアソン分布は
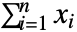 に等しい.ただし,
に等しい.ただし, は独立同分布に従う確率変数で dist に従い,nPoissonDistribution[λ]である.
は独立同分布に従う確率変数で dist に従い,nPoissonDistribution[λ]である. - CompoundPoissonDistributionでは,λ は任意の正の実数でよく,dist は任意の一変量分布でよい.
- CompoundPoissonDistributionは,Mean,Variance,RandomVariate等の関数で使うことができる.
予備知識
- CompoundPoissonDistribution[λ,dist]は,正の実数 λ と一変量分布 dist(連続分布でも離散分布でもよい)によってパラメータ化された離散統計分布を表す.複合ポアソン分布は,独立同分布に従う
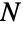 個の確率変数
個の確率変数 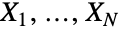 の和をモデル化する.ただし,すべての
の和をモデル化する.ただし,すべての 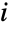 について Xidistであり,NPoissonDistribution[λ]である.母数 λ および dist は,形,高さ,位置,領域を含む,複合ポアソン分布の確率密度関数(PDF)が有するすべての特性を決定する.複合ポアソン分布は,ポアソン中断和,一般化されたポアソン分布,多重ポアソン分布,合成ポアソン分布,断続ポアソン分布,クラスタポアソン分布,Pollaczek–Geiringer分布,ポアソンベキ級数分布等,他のさまざまな名称で参照されることがある.
について Xidistであり,NPoissonDistribution[λ]である.母数 λ および dist は,形,高さ,位置,領域を含む,複合ポアソン分布の確率密度関数(PDF)が有するすべての特性を決定する.複合ポアソン分布は,ポアソン中断和,一般化されたポアソン分布,多重ポアソン分布,合成ポアソン分布,断続ポアソン分布,クラスタポアソン分布,Pollaczek–Geiringer分布,ポアソンベキ級数分布等,他のさまざまな名称で参照されることがある. - 複合ポアソン過程の研究は,Pollaczek–Geiringer分布の名称で,1930年代から行われている.複合ポアソン分布は,その初期には,事故,疾病,自殺を含む「稀な出来事」の統計動作のモデル化のためのツールとして考案された.確率過程の研究内で,複合ポアソン分布は,いわゆるベルヌーイ過程の開発動機ともなっている.ベルヌーイ過程は,大きさが指定された分布に従ってランダムに分布しているジャンプを持つ連続時間確率過程で,ジャンプはポアソン分布に従って現れる.より近年では,複合ポアソン分布のような中断和分布を使って,保険請求のタイプや頻度,降雨の頻度や量等を含むさまざまな現象のモデル化が行われている.
- RandomVariateを使って,複合ポアソン分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,CompoundPoissonDistribution[λ,dist]](より簡略すると xCompoundPoissonDistribution[λ,dist] )を使って,確率変数 x が複合ポアソン分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[CompoundPoissonDistribution[λ,dist],x] およびCDF[CompoundPoissonDistribution[λ,dist],x]を使って得られることがある.しかし,PDF(およびHazardFunctionやLikelihood等のPDF関連の数量)は,dist が連続分布の場合は定義されない.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができ,離散あるいは連続の dist のついて定義される.
- DistributionFitTestを使って,与えられたデータ集合が複合ポアソン分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリック複合ポアソン分布を推定することが,FindDistributionParametersを使ってデータを複合ポアソン分布にフィットすることができる.ProbabilityPlotを使って記号複合ポアソン分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号複合ポアソン分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された複合ポアソン分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って複合ポアソン分布を含む高次元分布を構築することが,ProductDistributionを使って複合ポアソン分布を含む独立成分分布の結合分布を計算することができる.
- CompoundPoissonDistributionは他の数多くの統計分布および構造と関連している.CompoundPoissonDistributionはPoissonDistributionを一般化したものである.母数 dist が任意の一変量分布を取れるため,CompoundPoissonDistributionとWolfram言語に含まれるすべての一変量分布との間には,包括的な関係がある.より具体的な意味で,CompoundPoissonDistributionは,CompoundPoissonProcess[λ,dist][t]を簡約するとCompoundPoissonDistribution[t λ,dist]になるという意味で,CompoundPoissonProcessのスライス分布である.さらに,Wolfram言語内のいくつかの分布は,dist のさまざまな値についてCompoundPoissonDistribution[λ,dist]から導くことができる.例として,BinomialDistribution(dist がBernoulliDistributionのとき),NegativeBinomialDistribution(dist がLogSeriesDistributionのとき)等が挙げられる.
例題
すべて開くすべて閉じるスコープ (7)
さまざまな更新率で複合ポアソン分布のシミュレーションを行う:
アプリケーション (2)
改装オープンした商店を訪れる顧客数は1時間に20人の割合でポアソン過程に従う.商店はこのイベントを販売促進に利用し,来店者全員に記念品を渡した.記念品の価値は,形状母数が10,尺度母数が3でワイブル分布に従う.改装オープン当日の開店時間12時間で渡された記念品にかかる費用総額の期待値を求める:
リスクからの支払い請求総計は,ポアソン母数200の複合ポアソン分布と,個々の請求額の分布(最小値母数300,形状母数3,位置母数0のパレート分布)に従う.保険者は損害再保険の超過分を保持レベル300ドルで発効させた.再保険会社の請求総額の平均と分散を計算する.再保険会社は300ドルを超えた額のみを支払うので,再保険会社への個別の請求は変形パレート分布に従う:
特性と関係 (5)
CompoundPoissonDistributionはCompoundPoissonProcessのスライス分布である:
BernoulliDistributionのCompoundPoissonDistributionはPoissonDistributionである:
特殊BorelTannerDistributionのCompoundPoissonDistributionはPoissonConsulDistributionに従う:
Borel–Tanner分布の変数の和はBorel–Tanner分布に従うので,スライス分布はパラメータ混合分布に等しい:
更新時がExponentialDistributionで与えられるCompoundRenewalProcessのスライス:
割合3で7におけるスライスについてのランダムなサンプルを作る:
対応するCompoundPoissonDistributionのサンプルと比較する:
テキスト
Wolfram Research (2012), CompoundPoissonDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/CompoundPoissonDistribution.html.
CMS
Wolfram Language. 2012. "CompoundPoissonDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CompoundPoissonDistribution.html.
APA
Wolfram Language. (2012). CompoundPoissonDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CompoundPoissonDistribution.html