DiscreteAsymptotic
DiscreteAsymptotic[expr,n∞]
n が整数上で無限大に近付くときの expr についての漸近近似を与える.
DiscreteAsymptotic[expr,{n,∞,m}]
expr についての漸近級数近似を次数 m まで与える.
詳細とオプション


- DiscreteAsymptoticは,主に,厳密解が求まらない問題を解くため,あるいは計算,比較,解釈等のためにより簡単な答を得るために使われる.そのような場合,漸近近似はしばしば該当する問題を簡約したり解いたりするために十分な情報を与える.
- DiscreteAsymptotic[expr,n∞]は,expr についての漸近展開における最高次の項を計算する.SeriesTermGoalを使うとより多くの項が指定できる.
- 式 expr は任意の数列
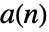 ,Sumで指定される総和,Productで指定される積,SeriesCoefficientで指定される数列,RSolveValue等で指定される差分方程式等でよい.
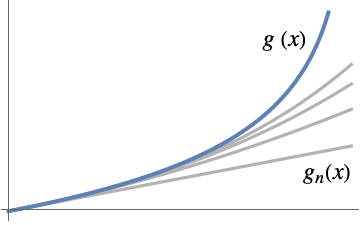
,Sumで指定される総和,Productで指定される積,SeriesCoefficientで指定される数列,RSolveValue等で指定される差分方程式等でよい. - 厳密結果が g[x]で x0における次数 n の漸近近似が gn[x]であれば,xx0のときにAsymptoticLess[g[x]-gn[x],gn[x]-gn-1[x],xx0]または g[x]-gn[x]∈o[gn[x]-gn-1[x]]である.
- 漸近近似 gn[x]はしばしば総和 gn[x]
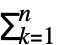 αkϕk[x]として与えられる.{ϕ1[x],…,ϕn[x]}は xx0のときの漸近尺度 ϕ1[x]≻ϕ2[x]≻⋯>ϕn[x]である.こうすると,xx0のとき AsymptoticLess[g[x]-gn[x],ϕn[x],xx0]または g[x]-gn[x]∈o[ϕn[x]]となる.
αkϕk[x]として与えられる.{ϕ1[x],…,ϕn[x]}は xx0のときの漸近尺度 ϕ1[x]≻ϕ2[x]≻⋯>ϕn[x]である.こうすると,xx0のとき AsymptoticLess[g[x]-gn[x],ϕn[x],xx0]または g[x]-gn[x]∈o[ϕn[x]]となる. - 次は,よく含まれる漸近尺度である.
-
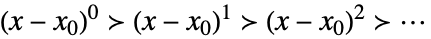
xx0のとき,テイラー(Taylor)スケール 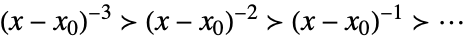
xx0のとき,ローラン(Laurent)スケール 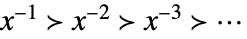
x±∞のとき,ローランスケール 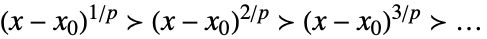
xx0のとき,ピュイゾー(Puiseux)スケール - 漸近近似を表すために使われる尺度は問題から自動的に推測される.多くの場合,より珍しい尺度を含めることができる.
- 次は,使用可能なオプションである.
-
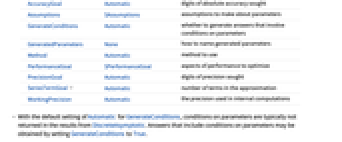
AccuracyGoal Automatic 目標確度 Assumptions $Assumptions パラメータについての仮定 GenerateConditions Automatic パラメータについての条件を含む答を生成するかどうか GeneratedParameters None 生成されたパラメータにどのように命名するか Method Automatic 使用するメソッド PerformanceGoal $PerformanceGoal パフォーマンスのどの面について最適化するか PrecisionGoal Automatic 目標精度 SeriesTermGoal Automatic 近似における項数 WorkingPrecision Automatic 内部計算の精度 - GenerateConditionsにデフォルト設定のAutomaticを使うと,Asymptoticからの結果には,一般に,パラメータについての条件が含まれない.GenerateConditionsをTrueにするとパラメータについての条件を含む答が得られることが多い.
- PerformanceGoalの可能な設定には,$PerformanceGoal,"Quality" ,"Speed"がある.このオプションを"Quality"に設定すると,DiscreteAsymptoticはより多くの問題を解いたりより簡単な答を生成したりするようになるが,かかる時間が長くなりメモリ消費量も大きくなる可能性がある.
- WorkingPrecision,AccuracyGoal,PrecisionGoalにデフォルト設定のAutomaticを使うと,たとえ入力精度が無限でも,DiscreteAsymptoticはより低い精度で漸近近似を返すかもしれない.
例題
すべて開くすべて閉じる例 (4)
![]() がInfinityに近付くときの
がInfinityに近付くときの ![]() の最高次の漸近項を求める:
の最高次の漸近項を求める:
SeriesTermGoalを使って展開からより多くの項を得る:
DiscreteAsymptoticを適用して漸近近似を計算する:
AsymptoticSumを使って同じ結果を得る:
AsymptoticRSolveValueを使って同じ結果を得る:
スコープ (19)
特殊数列 (6)
![]() がInfinityに近付くときの,Fibonacciについての最高次の漸近項を求める:
がInfinityに近付くときの,Fibonacciについての最高次の漸近項を求める:
Pochhammerについての最高次の漸近項:
HarmonicNumberの最高次の漸近項:
Zeta:
StirlingS1の最高次の漸近項:
BellBについての最高次の漸近項:
BernoulliBについての最高次の漸近項:
総和と総和変換 (3)
AsymptoticSumを使って同じ結果を得る:
差分方程式 (2)
オプション (1)
SeriesTermGoal (1)
アプリケーション (3)
特性と関係 (2)
DiscreteAsymptoticからの結果は数列と漸近的に等しい:
AsymptoticEquivalentを使って結果を確かめる:
DiscreteAsymptoticは,![]() の大きい値についての数列の挙動を説明する:
の大きい値についての数列の挙動を説明する:
DiscreteLimitは,Infinityにおける数列の挙動を説明する:
テキスト
Wolfram Research (2020), DiscreteAsymptotic, Wolfram言語関数, https://reference.wolfram.com/language/ref/DiscreteAsymptotic.html.
CMS
Wolfram Language. 2020. "DiscreteAsymptotic." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteAsymptotic.html.
APA
Wolfram Language. (2020). DiscreteAsymptotic. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteAsymptotic.html