FiniteFieldElement[ff,ind]
gives the element of the finite field ff with index ind.
FiniteFieldElement[ff,{c0,c1,c2,…}]
gives the element c0+c1θ+c2θ2+… of the finite field ff, where θ is the field generator of ff.


FiniteFieldElement
FiniteFieldElement[ff,ind]
gives the element of the finite field ff with index ind.
FiniteFieldElement[ff,{c0,c1,c2,…}]
gives the element c0+c1θ+c2θ2+… of the finite field ff, where θ is the field generator of ff.
Details

- FiniteFieldElement is used to represent an element in a FiniteField.
- FiniteFieldElement objects in the same field are automatically combined by arithmetic operations.
- Information[a,prop] or a[prop] gives the property prop of the FiniteFieldElement object a. The following properties can be specified:
-
"Field" the ambient field ff of a "Index" the index of a "Coefficients" {c0,c1,c2,…} where a=c0+c1θ+c2θ2+… "Characteristic" the characteristic p of ff "ExtensionDegree" the extension degree d of ff over 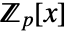
"FieldSize" the number of elements of ff "FieldIrreducible" the polynomial function f used to construct the field ff "ElementRepresentation" "Polynomial" or "Exponential" - MinimalPolynomial[a,x] gives the minimal degree monic polynomial in
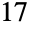 that is zero at a.
that is zero at a. - MultiplicativeOrder gives the multiplicative order of nonzero finite field elements.
- Polynomial operations such as PolynomialGCD, Factor, Expand, PolynomialQuotientRemainder and Resultant can be used for polynomials with finite field element coefficients. Together and Cancel can be used for rational functions with finite field element coefficients.
- Linear algebra operations such as Det, Inverse, RowReduce, NullSpace, MatrixRank and LinearSolve can be used for matrices with finite field element entries.
- Solve and Reduce can be used to solve systems of equations over finite fields.
Examples
open all close allBasic Examples (1)
Scope (13)
Representation and Properties (4)
Represent a finite field with characteristic ![]() and extension degree
and extension degree ![]() :
:
Specify an element of the field using polynomial coefficients:
Finite field elements are atomic objects:
Extract the polynomial coefficients and the field from a finite field element:
Specify an element of the field using an index:
Extract the index and the field from a finite field element:
Extract field properties from a finite field element:
Extract properties using Information:
Field additive and multiplicative identity elements have indices ![]() and
and ![]() :
:
Construct a finite field that uses exponential representation of elements:
All nonzero elements of the field are powers of the element with index ![]() :
:
Field additive and multiplicative identity elements have indices ![]() and
and ![]() :
:
Each element of ![]() can also be represented as a polynomial of degree
can also be represented as a polynomial of degree ![]() in
in ![]() :
:
Arithmetic (3)
Perform arithmetic operations in a finite field:
Rational powers work only with exponent denominators ![]() and
and ![]() :
:
For some field elements, the square root may not exist:
Arithmetic operations treat integers as elements of the field:
Rational numbers need to be valid modulo the field characteristic:
Use Element to decide which rational numbers can be identified with field elements:
For the purpose of comparison, rational numbers are identified with field elements:
Elements of different finite fields cannot be combined:
Fields with the same characteristic and field irreducible but different element representations are allowed:
Automorphisms and Embeddings (2)
Polynomials over Finite Fields (2)
Applications (8)
Implement an error-correcting code. The ![]() Hamming code encodes a
Hamming code encodes a ![]() -bit message in an
-bit message in an ![]() -bit sequence and is able to correct up to one error:
-bit sequence and is able to correct up to one error:
Let ![]() be a finite field with
be a finite field with ![]() elements using the exponential element representation, let
elements using the exponential element representation, let ![]() be the irreducible polynomial used to construct
be the irreducible polynomial used to construct ![]() , and let
, and let ![]() be the generator of
be the generator of ![]() :
:
The encoded message is the coefficient list of ![]() , where the coefficient list of
, where the coefficient list of ![]() is the original message:
is the original message:
Let ![]() be the polynomial whose coefficient list is the received message:
be the polynomial whose coefficient list is the received message:
If the received message contains no errors, then ![]() , and hence
, and hence ![]() :
:
If the received message contains one error in position ![]() , then
, then ![]() , and hence
, and hence ![]() :
:
Check and correct the received message:
To decode the message, compute the coefficient list of ![]() :
:
The decoded message is correct when the received message has no errors or one error:
Construct ![]() orthogonal Latin squares of order
orthogonal Latin squares of order ![]() for any prime power
for any prime power ![]() . A Latin square of order
. A Latin square of order ![]() is a
is a ![]() array such that each row and each column contains every element of a set of
array such that each row and each column contains every element of a set of ![]() elements exactly once. A pair of Latin squares is said to be orthogonal if the
elements exactly once. A pair of Latin squares is said to be orthogonal if the ![]() pairs formed by juxtaposing the two arrays are all distinct:
pairs formed by juxtaposing the two arrays are all distinct:
Verify that all arrays are Latin squares:
Verify that all pairs of arrays are orthogonal:
A finite set ![]() of integers is a Sidon set if the sums
of integers is a Sidon set if the sums ![]() for
for ![]() are all distinct. Construct a Sidon set of
are all distinct. Construct a Sidon set of ![]() integers in
integers in ![]() , for a prime power
, for a prime power ![]() :
:
Verify that ![]() is a Sidon set of length
is a Sidon set of length ![]() :
:
A de Bruijn sequence of order ![]() for an alphabet with
for an alphabet with ![]() letters is a cyclic sequence
letters is a cyclic sequence ![]() of
of ![]() letters of the alphabet, such that every sequence of
letters of the alphabet, such that every sequence of ![]() letters appears exactly once as a subsequence of
letters appears exactly once as a subsequence of ![]() . Construct a de Bruijn sequence of order
. Construct a de Bruijn sequence of order ![]() for an alphabet with
for an alphabet with ![]() letters, for a prime power
letters, for a prime power ![]() :
:
Verify that ![]() is a de Bruijn sequence of order
is a de Bruijn sequence of order ![]() for an alphabet with
for an alphabet with ![]() letters:
letters:
An ![]() matrix
matrix ![]() is a Hadamard matrix if all entries of
is a Hadamard matrix if all entries of ![]() are
are ![]() or
or ![]() and
and ![]() . Construct a Hadamard matrix of order
. Construct a Hadamard matrix of order ![]() for any prime power
for any prime power ![]() with
with ![]() :
:
Implement the Rijndael S-box step used in the Advanced Encryption Standard (AES) algorithm. The first part, called a Nyberg S-box, uses multiplicative inverse in ![]() :
:
The second part involves an affine transformation over ![]() :
:
The forward S-box is the composition of the two parts:
Compute the forward S-box table in the hexadecimal notation:
Define the inverse S-box transformation:
Compute the inverse S-box table in the hexadecimal notation:
Verify that the inverse S-box is the inverse of the forward S-box:
Implement a Diffie–Hellman public key cryptosystem with a 2049-bit prime:
Find a primitive element of the field ![]() :
:
The first user chooses a private key ![]() :
:
The public key consists of ![]() ,
, ![]() and
and ![]() :
:
To send a 2048-bit message ![]() , the second user sends
, the second user sends ![]() and
and ![]() :
:
The first user can recover ![]() by computing
by computing ![]() :
:
Implement a digital signature scheme. Fix a prime ![]() and find a primitive element
and find a primitive element ![]() of
of ![]() :
:
Pick a secret integer ![]() and publish
and publish ![]() ,
, ![]() and
and ![]() :
:
The signature for a message ![]() is a pair
is a pair ![]() of positive integers less than
of positive integers less than ![]() such that
such that ![]() . Computing the signature requires the knowledge of the secret integer
. Computing the signature requires the knowledge of the secret integer ![]() :
:
The signature can be verified using the publicly known information:
Properties & Relations (9)
A finite field with characteristic ![]() and extension degree
and extension degree ![]() has
has ![]() elements:
elements:
Elements of a finite field with characteristic ![]() satisfy
satisfy ![]() :
:
Hence the mapping ![]() is a field automorphism, known as FrobeniusAutomorphism:
is a field automorphism, known as FrobeniusAutomorphism:
The field generator ![]() is a root of the field irreducible:
is a root of the field irreducible:
Use FrobeniusAutomorphism to find the remaining roots of ![]() :
:
Use MinimalPolynomial to find the minimal polynomial of a finite field element:
The minimal polynomial over the subfield of ![]() with
with ![]() elements:
elements:
All elements of a finite field with ![]() elements are roots of
elements are roots of ![]() :
:
Any irreducible polynomial of degree ![]() over
over ![]() has
has ![]() roots in a field with
roots in a field with ![]() elements:
elements:
Use IrreduciblePolynomialQ with Modulusp to verify irreducibility over ![]() :
:
Use Factor with Extensionℱ to verify that f is a product of linear factors over ![]() :
:
Use MultiplicativeOrder to find the multiplicative order of finite field elements:
Use FiniteField[p,1] to compute over the prime field ![]() :
:
Compare with a result obtained using Mod:
Compare with a result obtained using the Modulus option:
Use FromFiniteFieldIndex to get field elements with specified indices:
FiniteFieldIndex gives indices of field elements:
Related Guides
Text
Wolfram Research (2023), FiniteFieldElement, Wolfram Language function, https://reference.wolfram.com/language/ref/FiniteFieldElement.html (updated 2024).
CMS
Wolfram Language. 2023. "FiniteFieldElement." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/FiniteFieldElement.html.
APA
Wolfram Language. (2023). FiniteFieldElement. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FiniteFieldElement.html
BibTeX
@misc{reference.wolfram_2025_finitefieldelement, author="Wolfram Research", title="{FiniteFieldElement}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/FiniteFieldElement.html}", note=[Accessed: 14-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_finitefieldelement, organization={Wolfram Research}, title={FiniteFieldElement}, year={2024}, url={https://reference.wolfram.com/language/ref/FiniteFieldElement.html}, note=[Accessed: 14-December-2025]}