Gamma
詳細

- 記号操作・数値操作の両方に適した数学関数である.
- ガンマ関数は,
![TemplateBox[{z}, Gamma]=int_0^inftyt^(z-1)e^(-t)dt TemplateBox[{z}, Gamma]=int_0^inftyt^(z-1)e^(-t)dt](Files/Gamma.ja/4.png) を満たす.
を満たす. - 不完全ガンマ関数は,
![TemplateBox[{a, z}, Gamma2]=int_z^inftyt^(a-1)e^(-t)dt TemplateBox[{a, z}, Gamma2]=int_z^inftyt^(a-1)e^(-t)dt](Files/Gamma.ja/5.png) を満たす.
を満たす. - 不完全一般ガンマ関数は,積分
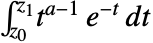 で与えられる.
で与えられる. - 不完全ガンマ関数Gammaの引数は,不完全ベータ関数Betaと異なる配列を取ることに注意.
- Gamma[z]は,不連続な分枝切断線を持たない.
- Gamma[a,z]は,複素 z 平面上,
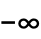 〜
〜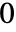 の範囲で不連続な分枝切断線を持つ.
の範囲で不連続な分枝切断線を持つ. - 特別な引数の場合,Gammaは,自動的に厳密値を計算する.
- Gammaは任意の数値精度で評価できる.
- Gammaは自動的にリストに縫い込まれる.
- GammaはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる. »
例題
すべて開くすべて閉じる例 (8)
Infinityにおける級数展開:
スコープ (50)
数値評価 (5)
Gammaを高精度で効率よく評価する:
IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する:
Aroundを使って平均的な場合における統計区間を計算することもできる:
MatrixFunctionを使って行列のGamma関数を計算することもできる:
特定の値 (5)
関数の特性 (10)
級数展開 (6)
オイラーのガンマ関数の ![]() の周りのテイラー(Taylor)展開:
の周りのテイラー(Taylor)展開:
オイラーのガンマ関数の ![]() の周りの最初の3つの近似をプロットする:
の周りの最初の3つの近似をプロットする:
オイラーのガンマ関数の無限大における級数展開(スターリングの近似):
Gammaはベキ級数に適用できる:
積分変換 (4)
LaplaceTransformを使って不完全ガンマ関数のラプラス(Laplace)変換を計算する:
不完全ガンマ関数のInverseLaplaceTransform:
不完全ガンマ関数のMellinTransform:
オイラーのガンマ関数のInverseMellinTransform:
関数の恒等式と簡約 (5)
関数表現 (5)
一般化と拡張 (6)
オイラーのガンマ関数 (3)
アプリケーション (9)
特性と関係 (7)
テキスト
Wolfram Research (1988), Gamma, Wolfram言語関数, https://reference.wolfram.com/language/ref/Gamma.html (2022年に更新).
CMS
Wolfram Language. 1988. "Gamma." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/Gamma.html.
APA
Wolfram Language. (1988). Gamma. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Gamma.html