GraphJoin
GraphJoin[g1,g2]
グラフ g1とグラフ g2のグラフ結合を与える.
詳細とオプション

- GraphJoinは完全和集合としても知られている.
- GraphJoinは,通常,到達可能な特定のサブグラフから新たなグラフを生成するために使われる.
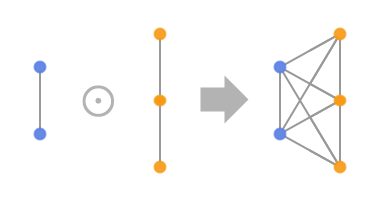
- GraphJoin[g1,g2]は g1の各頂点を g2のすべての頂点と繋ぐことで g1と g2から得られたグラフを与える.
- GraphJoin[g1,g2]はGraphDisjointUnion[g1,g2]を,IndexGraph[g1]の各頂点とIndexGraph[g2,n+1]の各頂点の間のすべての辺とともに返す.ここで,n はg1のVertexCountである.
- GraphJoinにはGraphと同じオプションが使える.
全オプションのリスト

例題
すべて開くすべて閉じるスコープ (29)
有向グラフ (5)
無向グラフ (5)
混合グラフ (5)
多重グラフ (5)
重み付きグラフ (5)
特性と関係 (4)
2つのグラフの隣接行列とその結合グラフを結合すると,GraphJoinの隣接行列が得られる:
Wolfram Research (2022), GraphJoin, Wolfram言語関数, https://reference.wolfram.com/language/ref/GraphJoin.html.
テキスト
Wolfram Research (2022), GraphJoin, Wolfram言語関数, https://reference.wolfram.com/language/ref/GraphJoin.html.
CMS
Wolfram Language. 2022. "GraphJoin." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GraphJoin.html.
APA
Wolfram Language. (2022). GraphJoin. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphJoin.html