HyperbolicDistribution
HyperbolicDistribution[α,β,δ,μ]
位置母数 μ,尺度母数 δ,形状母数 α,歪度母数 β の双曲線分布を表す.
HyperbolicDistribution[λ,α,β,δ,μ]
形状母数 λ の一般化された双曲線分布を表す.
詳細

- 双曲線分布における値
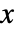 の確率密度は
の確率密度は 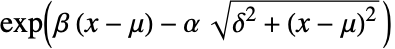 に比例する.
に比例する. - 一般化された双曲線分布における値
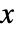 の確率密度は
の確率密度は ![ⅇ^(beta (x-mu))sqrt(delta^2+(x-mu)^2)^(lambda-1/2) TemplateBox[{{lambda, -, {1, /, 2}}, {alpha, , {sqrt(, {{delta, ^, 2}, +, {{(, {x, -, mu}, )}, ^, 2}}, )}}}, BesselK] ⅇ^(beta (x-mu))sqrt(delta^2+(x-mu)^2)^(lambda-1/2) TemplateBox[{{lambda, -, {1, /, 2}}, {alpha, , {sqrt(, {{delta, ^, 2}, +, {{(, {x, -, mu}, )}, ^, 2}}, )}}}, BesselK]](Files/HyperbolicDistribution.ja/4.png) に比例する.
に比例する. - HyperbolicDistributionでは,α と δ は任意の正の実数でよく,λ と μ は任意の実数でよく,β は
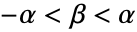 を満たす.
を満たす. - HyperbolicDistributionでは,α と β は単位次元が等しい任意の数量でよく,μ,δ,λ は α μ,α δ,λ 無次元になるような数量でよい. »
- HyperbolicDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- HyperbolicDistribution[λ,α,β,δ,μ]は,実数集合上で定義され正の実数 α(「形状母数」)および δ(「尺度母数」),および実数 λ(第2「形状母数」),μ(「位置母数」),
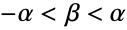 を満足する実数 β(「歪度母数」)によってパラメータ化された連続統計分布を表す.全体として,双曲線分布の確率密度関数(PDF)は滑らかで単峰型であるが,PDFグラフの特定の特性(水平位置,高さ,傾きの程度,凹面等)はさまざまな母数の値によって決定される.いわゆる形状母数の δ および λ は,PDFの形状に対してはっきりと異なるが同じような影響を与え,両者が組み合されてグラフの峰の周囲におけるPDFの集中度やPDFと
を満足する実数 β(「歪度母数」)によってパラメータ化された連続統計分布を表す.全体として,双曲線分布の確率密度関数(PDF)は滑らかで単峰型であるが,PDFグラフの特定の特性(水平位置,高さ,傾きの程度,凹面等)はさまざまな母数の値によって決定される.いわゆる形状母数の δ および λ は,PDFの形状に対してはっきりと異なるが同じような影響を与え,両者が組み合されてグラフの峰の周囲におけるPDFの集中度やPDFと 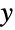 軸の近さ等を決定することは注目に値する.これに加え,双曲線分布のPDFの裾部は,PDFが
軸の近さ等を決定することは注目に値する.これに加え,双曲線分布のPDFの裾部は,PDFが 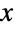 の大きい値については指数的に減少するがガウス分布(NormalDistributionを参照のこと)よりはゆっくり減少するという意味で「やや重い」.5つの母数を持ったHyperbolicDistributionは一般化された双曲線分布と呼ばれることがあるのに対し,4つの母数のHyperbolicDistribution[α,β,δ,μ] はHyperbolicDistribution[1,α,β,δ,μ]に等しく,一般に「双曲線分布」という場合はこれを指す.
の大きい値については指数的に減少するがガウス分布(NormalDistributionを参照のこと)よりはゆっくり減少するという意味で「やや重い」.5つの母数を持ったHyperbolicDistributionは一般化された双曲線分布と呼ばれることがあるのに対し,4つの母数のHyperbolicDistribution[α,β,δ,μ] はHyperbolicDistribution[1,α,β,δ,μ]に等しく,一般に「双曲線分布」という場合はこれを指す. - 双曲線分布の理論的な出発点は,1940年代初頭の博識なイギリス人であるR. A. Bagnoldまで遡ることができるが,デンマーク人の統計学者であるOle Barndorff-Nielsenによって実際に確率分布として確立されたのは,それからほぼ35年後の1970年代後半のことである.双曲線分布は,そのPDFの対数が双曲線であることによって特徴付けられる.双曲線分布は,特定の定性的情報以外が未知である理論分布の近似のために幅広く使われている.放物線分布および一般化された超幾何学分布の現実世界における最も基本的な使用例には,金融および株式における利益,株価変動,ポートフォリオのリスク,一般的な市場動向のモデル化が挙げられる.双曲線分布は,乱気流の風速や風に吹かれた砂の動き等の測定にも使われてきた.
- RandomVariateを使って,双曲線分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,HyperbolicDistribution[λ,α,β,δ,μ]](より簡略すると xHyperbolicDistribution[λ,α,β,δ,μ])を使って,確率変数 x が,双曲線分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[HyperbolicDistribution[λ,α,β,δ,μ],x]およびCDF[HyperbolicDistribution[λ,α,β,δ,μ],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合が双曲線分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータから双曲線パラメトリック分布を推定することが,FindDistributionParametersを使ってデータを双曲線分布にフィットすることができる.ProbabilityPlotを使って記号双曲線分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号双曲線分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された双曲線分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って双曲線分布を含む高次元分布を構築することが,ProductDistributionを使って双曲線分布を含む独立成分分布の結合分布を計算することができる.
- HyperbolicDistributionは,他の数多くの分布と密接に関連している.例えば,その一般性のゆえに,HyperbolicDistributionはLaplaceDistribution,StudentTDistribution,NormalDistribution,InverseGaussianDistribution,GammaDistribution,VarianceGammaDistribution,CauchyDistribution等の分布を,特殊なケースまたは極限のケースとして含んでいる.一般化されたHyperbolicDistributionは,また,HyperbolicDistribution[λ,α,β,δ,μ]のPDFがParameterMixtureDistribution[NormalDistribution[μ+β u,
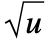 ],u InverseGaussianDistribution[δ/
],u InverseGaussianDistribution[δ/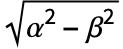 ,δ2,λ]]のそれと厳密に等しいという意味で,NormalDistributionおよびInverseGaussianDistributionの母数混合(ParameterMixtureDistributionを参照のこと)と見ることができる.HyperbolicDistributionは,ChiDistribution,ChiSquareDistribution,FRatioDistribution,HalfNormalDistributionとも関連している.
,δ2,λ]]のそれと厳密に等しいという意味で,NormalDistributionおよびInverseGaussianDistributionの母数混合(ParameterMixtureDistributionを参照のこと)と見ることができる.HyperbolicDistributionは,ChiDistribution,ChiSquareDistribution,FRatioDistribution,HalfNormalDistributionとも関連している.
例題
すべて開くすべて閉じる例 (6)
スコープ (10)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (5)
天然ダイヤモンドの直径(ミリメートル)の対数は,母数が![]() ,
,![]() ,
,![]() ,
,![]() でHyperbolicDistributionに従う:
でHyperbolicDistributionに従う:
正規逆ガウス(NIG)分布はHyperbolicDistributionの特殊ケースである:
このため,正規逆ガウス分布の変量の総和もまた正規逆ガウス分布に従う:
2005年からのS&P 500指数の日々の対数収益率を正規逆ガウス分布にフィットする:
分散ガンマ(Variance-gamma)分布[このデモンストレーションを参照のこと]は ![]() についての
についての ![]() の極限のケースである:
の極限のケースである:
組込みのVarianceGammaDistributionの確率密度関数と比較する:
一般化された双曲線(GH)歪 ![]() 分布は
分布は ![]() の極限において求められる:
の極限において求められる:
一般化された双曲線歪 ![]() 分布はまた母数を組み合せて表現することもできる:
分布はまた母数を組み合せて表現することもできる:
アメリカ合衆国の都市や町村の人口の対数はHyperbolicDistributionでモデル化することができる:
人口対数をHyperbolicDistributionにフィットする:
特性と関係 (9)
確率密度関数の対数は行列式の条件が![]() である一般化された双曲線方程式
である一般化された双曲線方程式 ![]() として書くことができる:
として書くことができる:
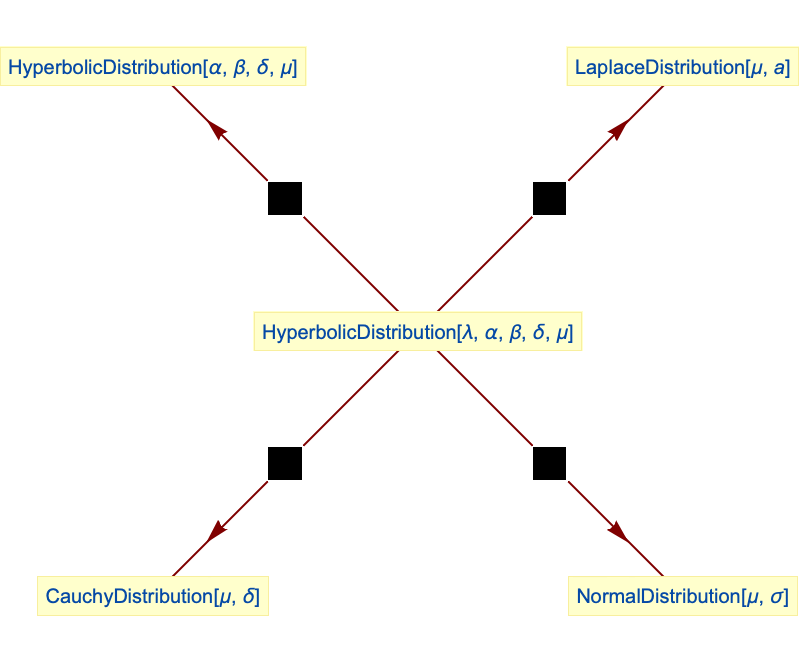
一般化された双曲線関数はNormalDistributionとInverseGaussianDistributionを変換したものである:
これは,ParameterMixtureDistributionとしても解釈できる:
CauchyDistributionは,![]() かつ
かつ ![]() であるなら,
であるなら,![]() の特異極限である:
の特異極限である:
NormalDistributionは,![]() かつ
かつ ![]() であるなら,
であるなら,![]() の極限状態である:
の極限状態である:
LaplaceDistributionは,![]() かつ
かつ ![]() であるなら,
であるなら,![]() の極限状態である:
の極限状態である:
テキスト
Wolfram Research (2010), HyperbolicDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/HyperbolicDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "HyperbolicDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/HyperbolicDistribution.html.
APA
Wolfram Language. (2010). HyperbolicDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HyperbolicDistribution.html