HyperbolicDistribution
✖
HyperbolicDistribution
更多信息
- 双曲分布中，值
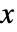的概率密度与 
成正比. - 广义双曲分布中，值
的概率密度与 ![ⅇ^(beta (x-mu))sqrt(delta^2+(x-mu)^2)^(lambda-1/2) TemplateBox[{{lambda, -, {1, /, 2}}, {alpha, , {sqrt(, {{delta, ^, 2}, +, {{(, {x, -, mu}, )}, ^, 2}}, )}}}, BesselK]](Files/HyperbolicDistribution.zh/4.png "ⅇ^(beta (x-mu))sqrt(delta^2+(x-mu)^2)^(lambda-1/2) TemplateBox[{{lambda, -, {1, /, 2}}, {alpha, , {sqrt(, {{delta, ^, 2}, +, {{(, {x, -, mu}, )}, ^, 2}}, )}}}, BesselK]")
成正比. - HyperbolicDistribution 允许 α 和 δ 为任意正实数，λ 和 μ 为任意实数，且 β 满足
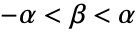. - HyperbolicDistribution 允许 α 和 β 为任何具有相同单位量纲的量，而 μ, δ, λ 是使得 α μ, α δ, 和 λ 为无量纲的量. »
- HyperbolicDistribution 可以和 Mean、CDF 和 RandomVariate 这样的函数一起使用.
背景
- HyperbolicDistribution[λ,α,β,δ,μ] 表示定义在一组实数上的一个连续统计分布：双曲分布. 它由以下参数决定：正实数 α（“形状参数”）和 δ（“尺度参数”）以及实数 λ（第二“形状参数”）、μ（“位置参数”）和 β（“偏斜度参数”），且满足
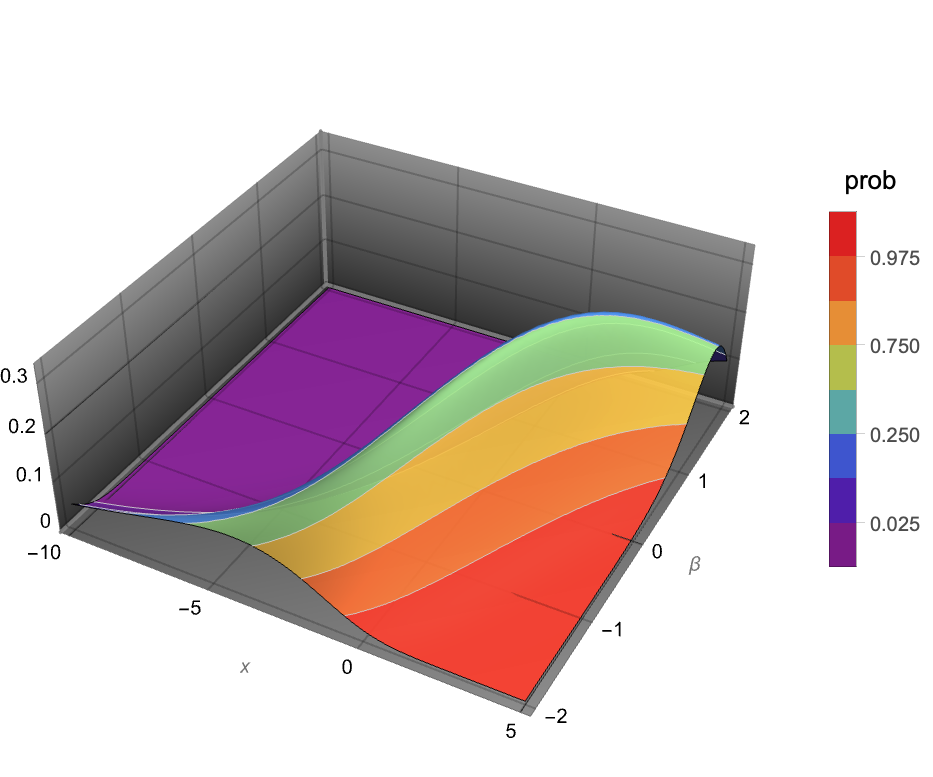
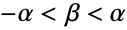. 总体上说，双曲分布的概率密度函数（PDF）是光滑且单峰的，虽然 PDF 图形的特定属性（如水平位置、高度、陡度和凹性）是由其各种参数的取值决定的. 值得注意的是，所谓的形状参数 δ 和 λ 对 PDF 的形状有着不同却相似的效果并共同决定了 PDF 在其峰值处图形的集中程度，以及 PDF 与 
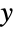轴的“接近程度”. 此外，双曲分布 PDF 的尾部是“半重型”的，意味着对较大的 
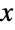值 PDF 的衰减是指数级的但比高斯分布衰减得要慢（参见 NormalDistribution）. 五参数版本的 HyperbolicDistribution 有时被称为广义双曲分布，而四参数版本的 HyperbolicDistribution[α,β,δ,μ] 等价于 HyperbolicDistribution[1,α,β,δ,μ] 并常被称为“那个”双曲分布. - 双曲分布理论根源可以追溯到 1940 年代早期英国博学家 R. A. Bagnold 的工作. 然而，它们被严格的宣布是概率分布发生在 35 年之后（1970 年代晚期），是丹麦统计学家 Ole Barndorff-Nielsen 的部分工作. 双曲分布的特征在于以下事实：其 PDF 的对数是双曲线. 除了某些定性信息之外，双曲分布已经被广泛用于在概率上逼近未知的理论分布. 双曲和广义超几何分布最基础的在现实世界的应用是在金融领域，在该领域中它们被用于对财务和股票回报率、价格走势、投资组合的风险、以及一般市场行为建模. 双曲分布也被用来测量湍流风速和风沙的移动.
- RandomVariate 可被用于给出双曲分布的一个或多个机器精度或任意精度（后者可用 WorkingPrecision 选项指定）的伪随机变量. Distributed[x,HyperbolicDistribution[λ,α,β,δ,μ]]，更简洁的写法是 xHyperbolicDistribution[λ,α,β,δ,μ]，可被用于声明随机变量 x 是双曲分布的. 这样一个声明之后可用在如 Probability、NProbability、Expectation 以及 NExpectation 这样的函数中.
- 概率密度函数和累积分布函数可用 PDF[HyperbolicDistribution[λ,α,β,δ,μ],x] 和 CDF[HyperbolicDistribution[λ,α,β,δ,μ],x] 求得. 平均数、中位数、方差、原点矩及中心矩可分别用 Mean、Median、Variance、Moment 和 CentralMoment 计算.
- DistributionFitTest 可被用于测试给定的数据集是否与双曲分布一致，EstimatedDistribution 可被用于根据给定数据估算双曲参数化分布，而 FindDistributionParameters 可拟合数据和双曲分布. ProbabilityPlot 可被用于生成给定数据的 CDF 相对于符号双曲分布的 CDF 的图线，而 QuantilePlot 可被用于生成给定数据的分位数相对于符号双曲分布的分位数的图线.
- TransformedDistribution 可被用于表示转换的双曲分布，CensoredDistribution 可被用于表示删截后位于上限值和下限值之间的值分布，而 TruncatedDistribution 可被用于表示截断后位于上限值和下限值之间的值分布. CopulaDistribution 可被用于建立包含了双曲分布的高维分布，而 ProductDistribution 可被用于计算包括双曲分布在内的，若干个独立分量的联合分布.
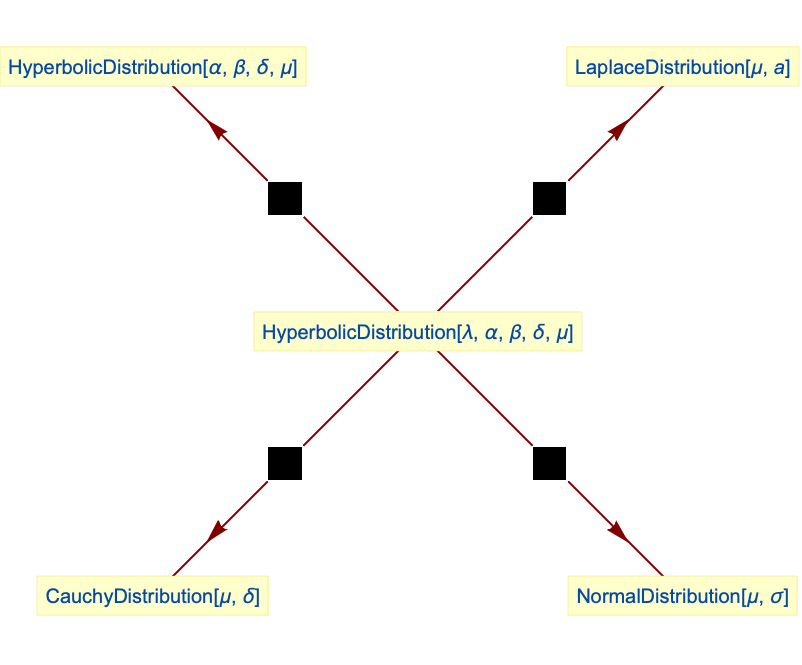
- HyperbolicDistribution 和许多其它分布密切相关. 例如，由于其一般性，HyperbolicDistribution 包含了如 LaplaceDistribution、StudentTDistribution、NormalDistribution、InverseGaussianDistribution、GammaDistribution、VarianceGammaDistribution 和 CauchyDistribution 等分布，或者作为特例，或者作为极限情形. 广义的 HyperbolicDistribution 也可被视为 NormalDistribution 和 InverseGaussianDistribution 的参数混合（参见 ParameterMixtureDistribution），这意味着 HyperbolicDistribution[λ,α,β,δ,μ] 的 PDF 精确等于 ParameterMixtureDistribution[NormalDistribution[μ+β u,
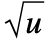],u InverseGaussianDistribution[δ/
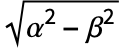,δ2,λ]]. HyperbolicDistribution 还和 ChiDistribution、ChiSquareDistribution、FRatioDistribution 及 HalfNormalDistribution 有关.
范例
打开所有单元关闭所有单元基本范例 (6)常见实例总结
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-9llvvn
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-geraqo
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh147wk89he92-mu25r4
Out[3]=3
In[1]:=1
✖
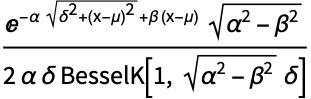
https://wolfram.com/xid/0bh147wk89he92-d55nzp
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-xi7pf5
Out[2]=2
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-l8rofy
Out[1]=1
In[2]:=2
✖
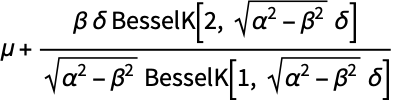
https://wolfram.com/xid/0bh147wk89he92-ttndhr
Out[2]=2
In[1]:=1
✖
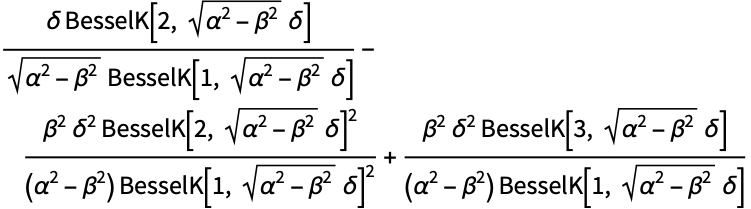
https://wolfram.com/xid/0bh147wk89he92-vgnu2i
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-s63qkg
Out[2]=2
In[1]:=1
✖
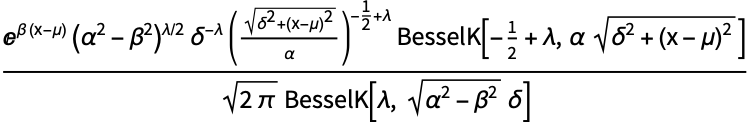
https://wolfram.com/xid/0bh147wk89he92-ptvj8v
Out[1]=1
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-m907xd
Out[1]=1
In[2]:=2
✖
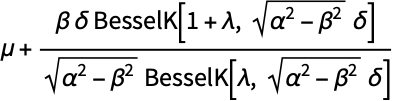
https://wolfram.com/xid/0bh147wk89he92-bq542m
Out[2]=2
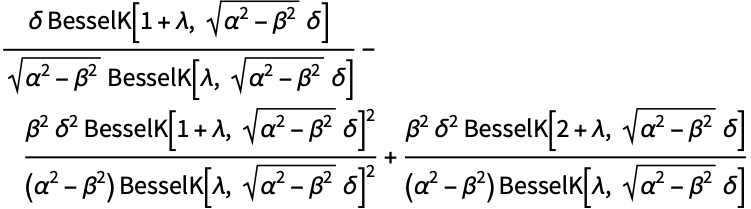
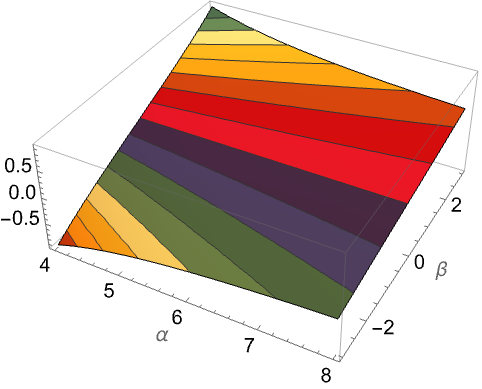
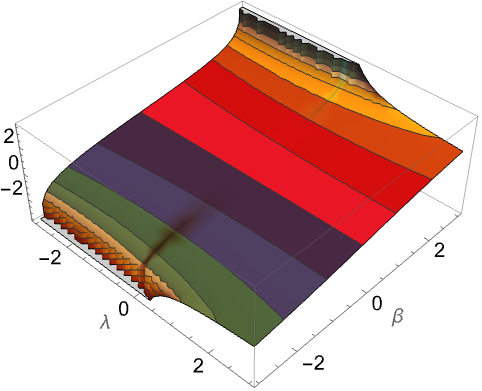
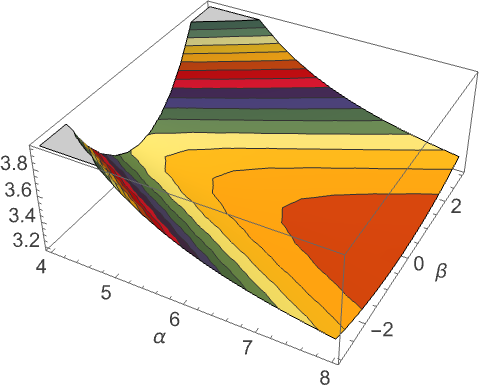
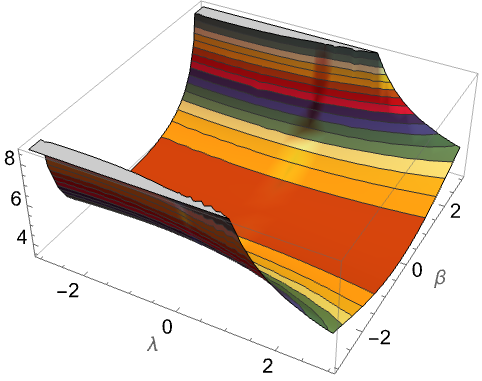
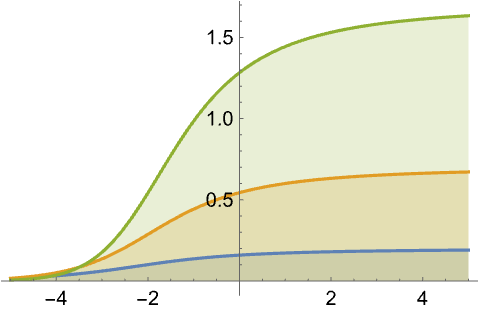
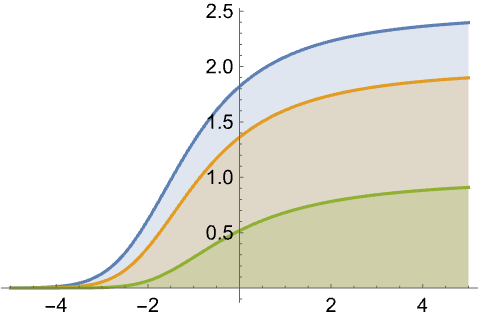
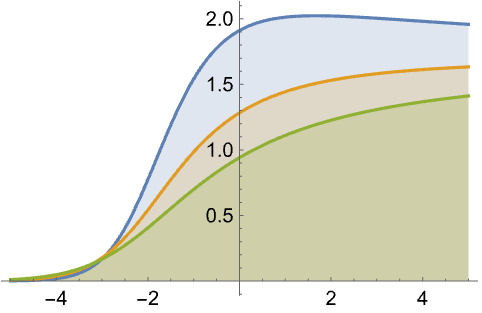
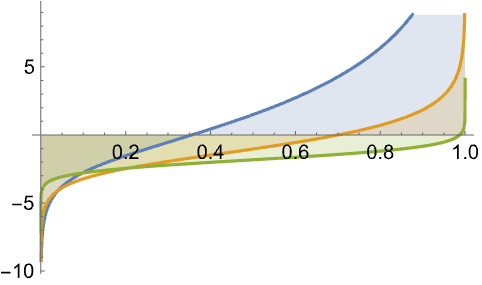
范围 (10)标准用法实例范围调查
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-0uu3ss
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-vdtzwq
Out[2]=2
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-45b7g2
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-epi747
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh147wk89he92-f8ui5o
Out[3]=3
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-8nrew
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-fzzss9
Out[2]=2
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-ke63qk
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-br8r0s
Out[2]=2
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-js043h
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-rx074o
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh147wk89he92-pknsqa
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0bh147wk89he92-zg9ct4
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0bh147wk89he92-9gzmth
Out[5]=5
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-nvil6w
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-rc97md
Out[2]=2
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-1ls7ux
Out[1]=1
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-nq5gh8
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-zb8rt1
Out[2]=2
In[1]:=1
✖
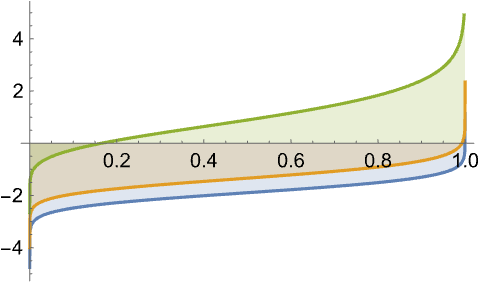
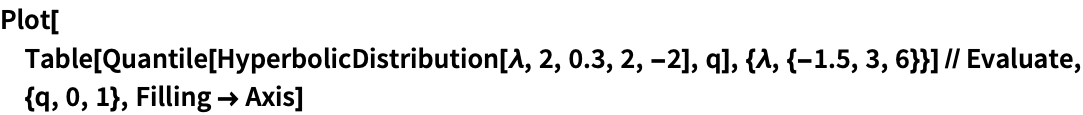
https://wolfram.com/xid/0bh147wk89he92-r6f1a7
Out[1]=1
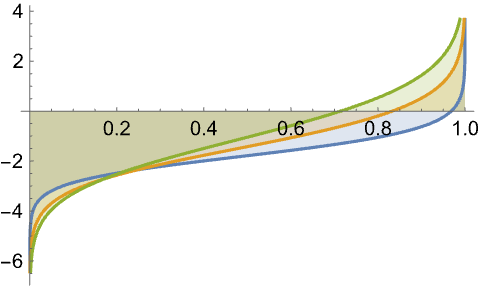
f参数中对 Quantity 保持一致的使用将给出 QuantityDistribution：
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-k7vlz
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-mevino
Out[2]=2
应用 (5)用该函数可以解决的问题范例
挖掘出来的钻石的直径（以毫米为单位）的对数服从 HyperbolicDistribution，其中参数 
、
、
和 
：
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-c5bng8
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-quktc
In[3]:=3
✖
https://wolfram.com/xid/0bh147wk89he92-g296yu
Out[3]=3
In[4]:=4
✖
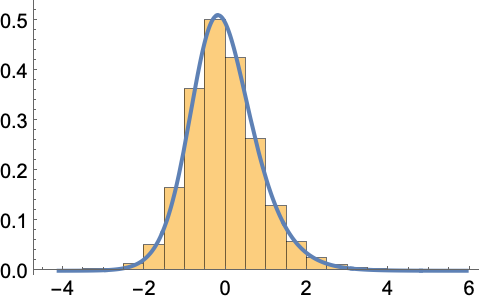
https://wolfram.com/xid/0bh147wk89he92-fwzgwi
Out[4]=4
正态逆高斯（NIG）分布是 HyperbolicDistribution 的特例：
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-bt40o8
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-b92klk
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh147wk89he92-510ax
Out[3]=3
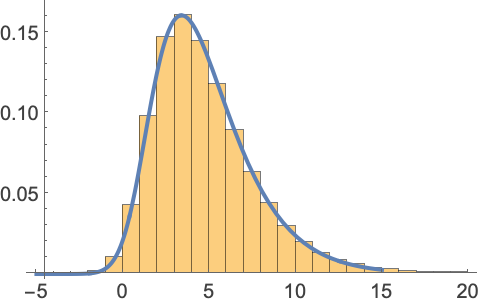
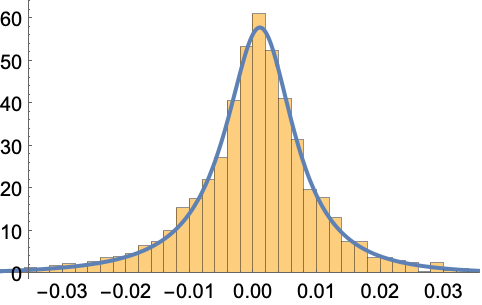
将 2005 年以来的标普 500 指数的每日对数收益进行 NIG 分布拟合：
In[4]:=4
✖
https://wolfram.com/xid/0bh147wk89he92-d7x402
In[5]:=5
✖
https://wolfram.com/xid/0bh147wk89he92-ef4yyh
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0bh147wk89he92-cz7d7o
Out[6]=6
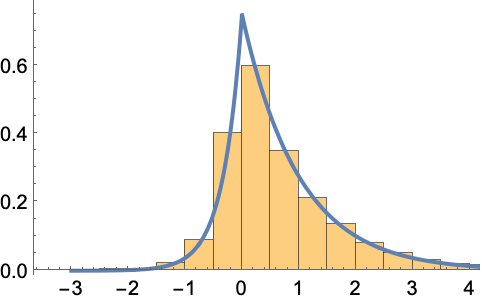
方差-伽玛分布 (参见演示) 是在 
时 
的极限情况：
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-c8dyjs
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-76ko3
In[3]:=3
✖
https://wolfram.com/xid/0bh147wk89he92-qkwega
Out[3]=3
与内置的 VarianceGammaDistribution 改良分布函数做比较
In[4]:=4
✖
https://wolfram.com/xid/0bh147wk89he92-fq1fpv
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0bh147wk89he92-ja8ava
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0bh147wk89he92-mxdwi6
Out[6]=6
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-bsj9k
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-efnzgk
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh147wk89he92-b8yrq1
In[4]:=4
✖
https://wolfram.com/xid/0bh147wk89he92-ec25x2
Out[4]=4
In[5]:=5
✖
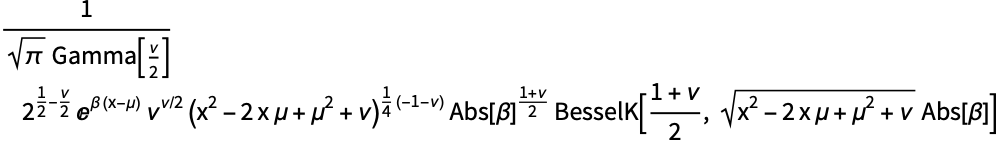
https://wolfram.com/xid/0bh147wk89he92-bh9y4u
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0bh147wk89he92-5bned
Out[6]=6
In[7]:=7
✖
https://wolfram.com/xid/0bh147wk89he92-o78xjz
Out[7]=7
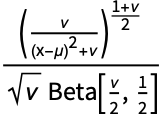
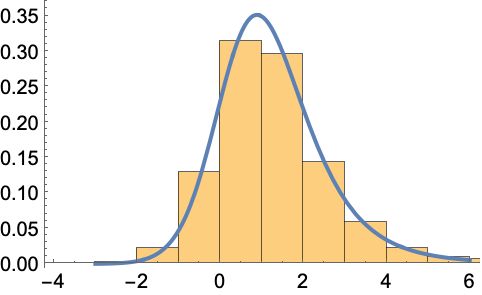
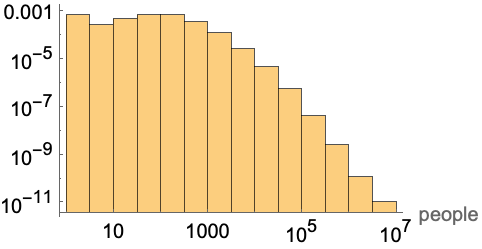
美国镇、城、村的人口数目的对数值可以用 HyperbolicDistribution 建模：
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-bogmpv
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-ch20yl
In[3]:=3
✖
https://wolfram.com/xid/0bh147wk89he92-dugf56
Out[3]=3
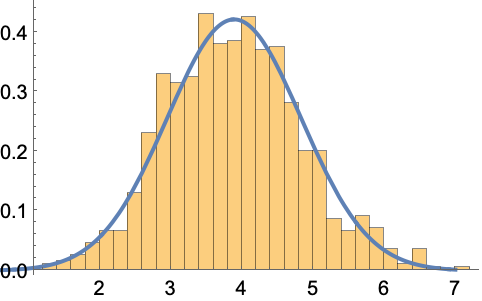
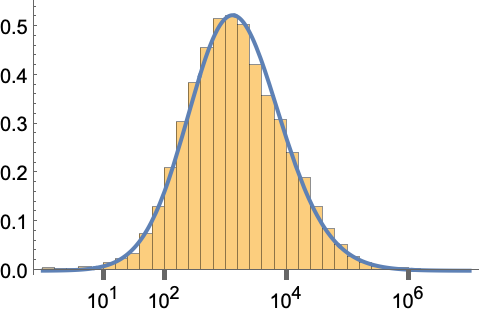
对人口数目的对数进行 HyperbolicDistribution 拟合：
In[4]:=4
✖
https://wolfram.com/xid/0bh147wk89he92-eqdffl
In[5]:=5
✖
https://wolfram.com/xid/0bh147wk89he92-ftna4x
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0bh147wk89he92-c9y05
Out[6]=6
属性和关系 (9)函数的属性及与其他函数的关联
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-6w68us
Out[1]=1
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-gh52pz
Out[1]=1
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-bl2ykz
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-beshfk
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh147wk89he92-viqjs6
Out[3]=3
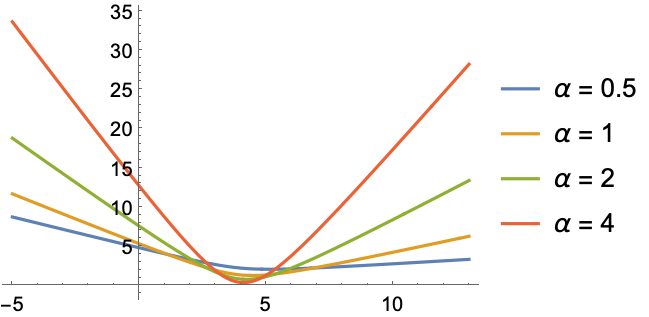
概率密度函数的对数可以写为一个通用双曲线方程 
，其中判定条件是 ![TemplateBox[{{(, , {{Axx, , Axy}, ; , {Axy, , Ayy}}, , )}}, Det]<0](Files/HyperbolicDistribution.zh/23.png "TemplateBox[{{(, , {{Axx, , Axy}, ; , {Axy, , Ayy}}, , )}}, Det]<0"){kind=small}
：
In[4]:=4
✖
https://wolfram.com/xid/0bh147wk89he92-eo79ge
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0bh147wk89he92-l7ayxb
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0bh147wk89he92-r0zqow
Out[6]=6
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-qo8iwl
Out[1]=1
In[2]:=2
✖
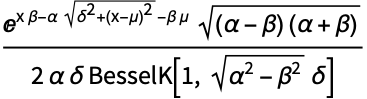
https://wolfram.com/xid/0bh147wk89he92-guesso
Out[2]=2
In[3]:=3
✖
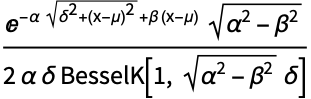
https://wolfram.com/xid/0bh147wk89he92-lnpb3s
Out[3]=3
广义双曲分布是 NormalDistribution 和 InverseGaussianDistribution 的变换：
In[1]:=1
✖
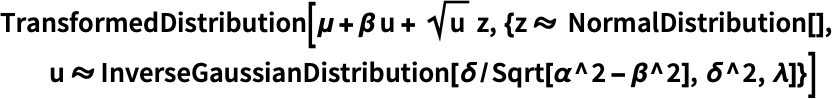
https://wolfram.com/xid/0bh147wk89he92-dgg6mj
Out[1]=1
它也可以被解释为 ParameterMixtureDistribution：
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-c1sbnm
In[3]:=3
✖
https://wolfram.com/xid/0bh147wk89he92-tgvk99
Out[3]=3
In[4]:=4
✖
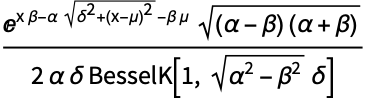
https://wolfram.com/xid/0bh147wk89he92-ez8075
Out[4]=4
In[5]:=5
✖
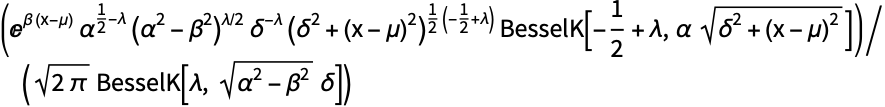
https://wolfram.com/xid/0bh147wk89he92-dnbhjl
Out[5]=5
当 
和 
时，CauchyDistribution 是 
的一个奇异极限：
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-zaivr
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-t0i98t
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh147wk89he92-864usd
Out[3]=3
当 
和 
时，NormalDistribution 是 
的极限情况：
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-b1jazy
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-mu1v5w
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh147wk89he92-opm24h
Out[3]=3
当 
和 
时，LaplaceDistribution 是 
的极限情况：
In[1]:=1
✖
https://wolfram.com/xid/0bh147wk89he92-bp13cv
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh147wk89he92-o9nydr
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh147wk89he92-ceglxf
Out[3]=3
Wolfram Research (2010)，HyperbolicDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HyperbolicDistribution.html （更新于 2016 年）.
✖
Wolfram Research (2010)，HyperbolicDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HyperbolicDistribution.html （更新于 2016 年）.文本
Wolfram Research (2010)，HyperbolicDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HyperbolicDistribution.html （更新于 2016 年）.
✖
Wolfram Research (2010)，HyperbolicDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HyperbolicDistribution.html （更新于 2016 年）.CMS
Wolfram 语言. 2010. "HyperbolicDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/HyperbolicDistribution.html.
✖
Wolfram 语言. 2010. "HyperbolicDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/HyperbolicDistribution.html.APA
Wolfram 语言. (2010). HyperbolicDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HyperbolicDistribution.html 年
✖
Wolfram 语言. (2010). HyperbolicDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HyperbolicDistribution.html 年BibTeX
✖
@misc{reference.wolfram_2025_hyperbolicdistribution, author="Wolfram Research", title="{HyperbolicDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/HyperbolicDistribution.html}", note=[Accessed: 17-April-2025
]}BibLaTeX
✖
@online{reference.wolfram_2025_hyperbolicdistribution, organization={Wolfram Research}, title={HyperbolicDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/HyperbolicDistribution.html}, note=[Accessed: 17-April-2025
]}