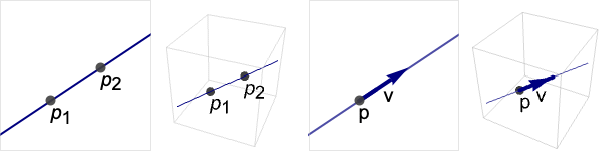
InfiniteLine

InfiniteLine[{p1,p2}]

点 p1および p2を通る無限の直線を表す．

InfiniteLine[p,v]

点 p を通り v 方向に進む無限の直線を表す．

詳細

  • InfiniteLineは線としても知られている．
  • InfiniteLineは，幾何学領域として，またグラフィックスプリミティブとして使うことができる．
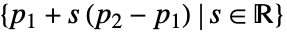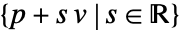  • InfiniteLineは，線形曲線あるいはを表す．
  • Hyperplane[n,p]は2Dで法線 n を使った別の表現である．
  • InfiniteLineはGraphicsおよびGraphics3Dで使うことができる．
  • InfiniteLineは，描画される際はPlotRangeで切り取られる．
  • グラフィックスでは，点 p，piおよびベクトル v はDynamic式でもよい．
  • グラフィックスの描画は，Thickness，Dashing，色等の指示子の影響を受ける．
  • InfiniteLineはGeometricSceneの記号的な点と一緒に使うことができる．

例題

すべて開くすべて閉じる

例  (3)

2DにおけるInfiniteLine：

3Dにおけるもの：

異なるスタイルが適用された無限直線：

無限直線における点の帰属判定：

スコープ  (19)

グラフィックス  (8)

指定  (3)

を含み，の方向に進むInfiniteLineを定義する：

およびを通る同じ線を定義する：

を含み，の方向に進む3Dの無限直線を定義する：

点およびを使って同じ無限直線を定義する：

方向が異なる無限直線：

スタイリング  (4)

スケールされたサイズによる太さ：

印刷用ポイント数による太さ：

破線あるいは点線スタイルを使って無限直線を描画することができる：

無限直線の色の指定に色指示子を用いることができる：

さまざまな指示子を組み合せて無限直線にスタイルを与える：

座標  (1)

点およびベクトルはDynamicでよい：

領域  (11)

埋込み次元は頂点の次元である：

幾何次元は領域の次元である：

点の帰属判定：

帰属条件を得る：

無限直線は有界ではない：

領域範囲を求める：

InfiniteLineの測度は無限である：

点からの距離：

領域までのプロット距離：

点からの符号付き距離：

最近点までの距離：

領域内の最近点：

最近点を可視化する：

無限直線上で積分する：

無限直線上で最適化する：

無限直線上で方程式を解く：

アプリケーション  (17)

に並ぶ平行線を作成する：

漸近線を示す：

線の切片型をInfiniteLineに変換する：

線を可視化する：

線の点傾き型をInfiniteLineに変換する：

線を可視化する：

線の傾き切片型をInfiniteLineに変換する：

線を可視化する：

線の2点型をInfiniteLineに変換する：

線を可視化する：

線のパラメトリック型をInfiniteLineに変換する：

線を可視化する：

パラメトリック曲線 f[u]に対する接線はInfiniteLine[f[u],f'[u]]で与えられる．パラメトリック曲線に対する接線を求める：

パラメトリック曲線についての接線を求める：

InfiniteLine[{0,0},{1,1}]とInfiniteLine[{{0,1},{1,0}}]の交点を求める：

これをプロットする：

InfiniteLine[{0,0},{1,1}]とCircle[{0,0},1]の交点を求める：

これをプロットする：

5本のランダムな線のすべてのペアについての交点を求める：

BooleanCountingFunctionを使い，厳密に2つの条件が真であることを表す：

これをプロットする：

InfiniteLine[{{-1,1,1},{1,1,1}}]とInfinitePlane[{{2,0,0},{0,2,0},{0,0,2}}]の交点を求める：

これをプロットする：

InfiniteLine[{{-1,1,1},{1,1,1}}]とSphere[{0,0,0},3]の交点を求める：

これをプロットする：

InfiniteLine[{{-1,1/3,1/2},{1,1/3,1/2}}]とTetrahedron[{{0,0,0},{1,0,0},{0,1,0},{0,0,1}}]の境界との交点を求める：

これをプロットする：

Histogram上のMeanを示す：

RotationTransformの回転軸を可視化する：

三角形の高さを求める：

高さを赤で可視化する：

特性と関係  (5)

InfiniteLine[{p1,p2}]はInfiniteLine[p1,p2-p1]に等しい：

InfiniteLine[p,v]は2DのHyperplane[Cross[v],p]に等しい：

ParametricRegionは任意のInfiniteLineを表すことができる：

ImplicitRegionは任意のInfiniteLineを表すことができる：

InfiniteLineはConicHullRegionの特殊ケースである：

おもしろい例題  (2)

線のランダムな集合：

線の構造化された集合：

Wolfram Research (2014), InfiniteLine, Wolfram言語関数， https://reference.wolfram.com/language/ref/InfiniteLine.html.

テキスト

Wolfram Research (2014), InfiniteLine, Wolfram言語関数， https://reference.wolfram.com/language/ref/InfiniteLine.html.

CMS

Wolfram Language. 2014. "InfiniteLine." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InfiniteLine.html.

APA

Wolfram Language. (2014). InfiniteLine. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InfiniteLine.html

BibTeX

@misc{reference.wolfram_2024_infiniteline, author="Wolfram Research", title="{InfiniteLine}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/InfiniteLine.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_infiniteline, organization={Wolfram Research}, title={InfiniteLine}, year={2014}, url={https://reference.wolfram.com/language/ref/InfiniteLine.html}, note=[Accessed: 17-November-2024 ]}