InverseLaplaceTransform

InverseLaplaceTransform[F[s],s,t]

変数 s におけるF[s]の記号逆ラプラス変換を変数 t における f[t]として与える．

InverseLaplaceTransform[F[s],s,]

数値 における記号逆ラプラス変換を与える．

InverseLaplaceTransform[F[s1,…,sn],{s1,s2,…},{t1,t2,…}]

F[s1,…,sn]の多次元逆ラプラス変換を与える．

詳細とオプション

  • ラプラス変換は，微分方程式および偏微分方程式を代数方程式に変換して解き，解に逆変換し直す際にしばしば用いられる．
  • ラプラス変換は，制御理論と信号処理においても，伝達関数・伝達行列の形で線形系を表現・操作する方法として広く使われている．つまり，ラプラス変換とその逆変換は時間領域と周波数領域の間の変換手段なのである．
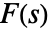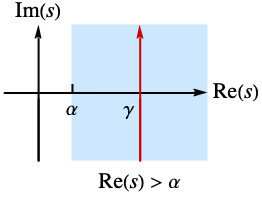
  • 関数 の逆ラプラス変換は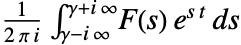， で定義される．ここで γ は積分路が 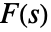のすべての特異点の右にあるように選ばれるような任意の正定数である．
  • 関数 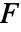の多次元逆ラプラス変換は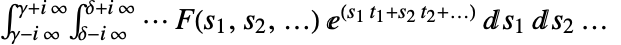の形の線積分として与えられる．
  • 積分は，第3引数の が数値として与えられたときは数値メソッドを使って計算される．使用可能なメソッドには，"Crump"，"Durbin"，"Papoulis"，"Piessens"，"Stehfest"，"Talbot"，"Weeks"がある．
  • 漸近逆ラプラス変換はAsymptoticを使って計算できる．
  • 次は，使用可能なオプションである．
  • AccuracyGoalAutomatic目標絶対確度の桁数
    Assumptions$Assumptionsパラメータについての仮定
    GenerateConditions Falseパラメータについての条件を含む答を生成するかどうか
    Method Automatic使用するメソッド
    PerformanceGoal$PerformanceGoal最適化するパフォーマンスの局面
    PrecisionGoalAutomatic目標精度の桁数
    WorkingPrecisionAutomatic内部計算精度
  • TraditionalFormでは，InverseLaplaceTransformは ℒ-1を使って出力される． »

例題

すべて開くすべて閉じる

例  (4)

関数の逆ラプラス変換を計算する：

パラメータがある関数の逆ラプラス変換：

結果をプロットする：

数値による逆ラプラス変換を計算する：

二変量関数の逆ラプラス変換：

スコープ  (56)

基本的な用法  (3)

関数の逆ラプラス変換を記号パラメータ t について計算する：

パラメータに数値を使う：

TraditionalFormによる表示：

有理関数  (5)

線形関数の逆数：

二次関数の逆数：

逆関数が三角関数である関数：

逆関数が双曲線関数である関数：

さらに有理関数の例：

初等関数  (5)

平方根を含む関数：

指数関数と平方根関数を含む関数：

その他の代数関数：

逆ラプラス変換はベッセル(Bessel)関数に繋がる：

逆正接関数の逆関数：

対数関数  (4)

対数関数の逆ラプラス変換：

有理関数の対数：

結果をプロットする：

対数関数とベキ関数の積：

対数の平方根を含む関数：

特殊関数  (12)

BesselKを含む関数：

不完全ガンマ関数とベキ関数の割合：

ポリガンマ関数の逆関数：

誤差関数を含む関数の逆関数：

平方根関数からなる誤差関数：

LegendreP関数とLegendreQ関数の逆変換：

ルジャンドル関数の複素数プロット：

BesselIとExpの積：

周波数領域関数のComplexPlot：

BesselJ関数とGamma関数の積：

周波数領域関数のComplexPlot：

指数積分関数と平方根関数の組合せ：

2つのParabolicCylinderD関数の積：

楕円積分関数を含む逆変換：

EllipticThetaの逆変換：

区分関数  (5)

次の関数の逆関数は区分関数である：

逆関数をプロットする：

指数関数の逆関数はボックス関数に繋がる：

指数関数の逆関数は区分三角関数に繋がる：

逆関数は階段関数に繋がる：

その他の階段関数を含む例：

周期関数  (4)

次の関数の逆関数は t について周期的である：

和をアクティブにする：

プロットして結果が矩形波であることを確認する：

逆関数が正弦関数の絶対値である関数：

結果をアクティブにしてプロットする：

逆関数が台形波である関数：

その他の区分関数に含まれる例：

一般化された関数  (3)

指数関数の逆関数はディラック(Dirac)関数である：

指数関数と s のベキの積の逆関数はディラック関数の導関数である：

双曲線正割関数の逆関数は一連のディラック関数である：

双曲線余接関数：

多変量関数  (8)

二変量有理関数の逆ラプラス変換：

結果を確かめる：

p と q について分割可能な有理関数：

p と q について分割不可能な有理関数：

逆関数がBesselJに関連している有理関数：

累乗根を含む二変量関数の逆ラプラス変換：

3変数の多変量関数の逆ラプラス変換：

有理関数：

対数を含む関数：

数値反転  (4)

単一の点の逆ラプラス変換を計算する：

逆ラプラス変換を記号的に計算することもできる：

次に，t の特定の値について評価する：

逆ラプラス変換を数値的に求め，厳密な結果と比較する：

逆関数が t について区分関数である関数：

逆関数が t について周期的である関数：

非整数階微積分  (3)

領域における代数関数のComplexPlot：

この代数関数の逆ラプラス変換：

領域へのラプラス変換：

代数関数の逆ラプラス変換：

時間領域でプロットする：

領域へのラプラス変換：

パラメータを含む代数関数の逆ラプラス変換：

領域へのラプラス変換：

オプション  (3)

GenerateConditions  (1)

デフォルトで，InverseLaplaceTransformは結果が非負の t について定義されると仮定する：

GenerateConditionsを使って結果の有効性の範囲を入手する：

Method  (1)

数値評価にデフォルトメソッドを使う：

Methodを使って異なるメソッドの結果を入手する：

Working Precision  (1)

WorkingPrecisionを使って任意精度の結果を入手する：

アプリケーション  (5)

伝達関数で線形系に対するステップ応答を計算する：

微分方程式をラプラス変換を用いて解く：

ラプラス変換について解く：

逆変換を求める：

初期条件を適用する：

DSolveを直接用いて解を求める：

3/2階の非整数階微分方程式を解く：

ラプラス変換について解く：

逆変換を求める：

解をプロットする：

DSolveを使って解を直接求める：

21/10階の非整数階微分方程式を解く：

ラプラス変換について解く：

逆変換を求める：

解をプロットする：

DSolveを使って解を直接求める：

LaplaceTransformを使って非整数階微分方程式系を解く：

逆変換を求める：

特性と関係  (2)

Asymptoticを使って漸近近似を計算する：

InverseLaplaceTransformとLaplaceTransformは互いに逆関数である：

おもしろい例題  (2)

MeijerG関数のInverseLaplaceTransform：

基本的な逆ラプラス変換の表を作成する：

Wolfram Research (1999), InverseLaplaceTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseLaplaceTransform.html （2023年に更新）.

テキスト

Wolfram Research (1999), InverseLaplaceTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseLaplaceTransform.html （2023年に更新）.

CMS

Wolfram Language. 1999. "InverseLaplaceTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/InverseLaplaceTransform.html.

APA

Wolfram Language. (1999). InverseLaplaceTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseLaplaceTransform.html

BibTeX

@misc{reference.wolfram_2024_inverselaplacetransform, author="Wolfram Research", title="{InverseLaplaceTransform}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/InverseLaplaceTransform.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_inverselaplacetransform, organization={Wolfram Research}, title={InverseLaplaceTransform}, year={2023}, url={https://reference.wolfram.com/language/ref/InverseLaplaceTransform.html}, note=[Accessed: 21-November-2024 ]}