Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

LineIntegrate

LineIntegrate[f,{x,y,…}∈curve]

计算函数 f[x,y,…] 在 curve 上的标量线积分.

LineIntegrate[{p,q,…},{x,y,…}∈curve]

计算矢量函数 {p[x,y,…],q[x,y,…],…} 的矢量线积分.

更多信息和选项

线积分也称为曲线积分和功积分.
标量线积分沿曲线对标量函数进行积分，通常用于计算曲线的长度、质量和电荷.
矢量线积分用于计算矢量函数沿曲线在其切线方向移动时所做的功. 典型的矢量函数包括力场、电场和流体速度场.
函数 f 沿 curve 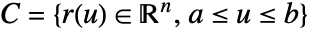的标量线积分由下式给出：

其中 $TemplateBox[{{{r, ^, {(, ', )}}, (, u, )}}, Norm]$ 是参数曲线段的度量.
标量线积分与 curve 的参数化和方向无关. 任何一维 RegionQ 对象都可以用作 curve.
函数 F 沿曲线 curve 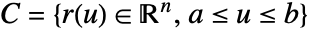的矢量线积分由下式给出：

其中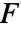是矢量函数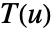在切线方向上的投影，因此只有切线方向的分量被积分.
矢量线积分与曲线的参数化无关，但确实取决于曲线的方向.
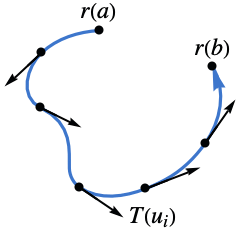
曲线的方向由曲线上的切线矢量场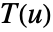给出.

对于参数曲线 ParametricRegion[{r₁[u],…,r_n[u]},…]，切矢量场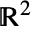取作 ∂_ur[u].
中具有假定切线方向的特殊曲线包括：

		Line[{p₁,p₂,…}]	方向按照点从 p₁ 到 p₂ 等给出的顺序.
		HalfLine[{p₁,p₂}] HalfLine[p,v]	方向是从 p₁ 到 p₂，或在 v 方向
		InfiniteLine[{p₁,p₂}] InfiniteLine[p,v]	方向是从 p₁ 到 p₂，或在 v 方向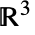
		Circle[p,r]	方向是逆时针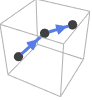

中具有假定切线方向的特殊曲线包括：

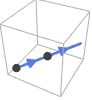
		Line[{p₁,p₂,…}]	方向按照点从 p₁ 到 p₂ 等给出的顺序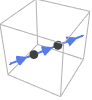
		HalfLine[{p₁,p₂}] HalfLine[p,v]	方向是从 p₁ 到 p₂，或在 v 方向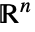
		InfiniteLine[{p₁,p₂}] InfiniteLine[p,v]	方向是从 p₁ 到 p₂，或在 v 方向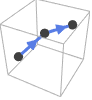

中具有假定切线方向的特殊曲线包括：

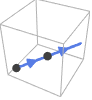
		Line[{p₁,p₂,…}]	方向按照给定的点的顺序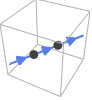
		HalfLine[{p₁,p₂}] HalfLine[p,v]	方向是从 p₁ 到 p₂ 方向由 v 给出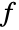
		InfiniteLine[{p₁,p₂}] InfiniteLine[p,v]	方向是从 p₁ 到 p₂ 方向由 v 给出

沿 curve 的坐标可以使用 VectorSymbol 指定. »
可以给出以下选项：

	Assumptions	$Assumptions	关于参数的假设
	Direction	Automatic	曲线的方向
	GenerateConditions	Automatic	是否生成涉及参数条件的答案
	WorkingPrecision	Automatic	内部计算中使用的精度

当输入涉及不精确的数量时，LineIntegrate 使用符号和数值方法的组合.

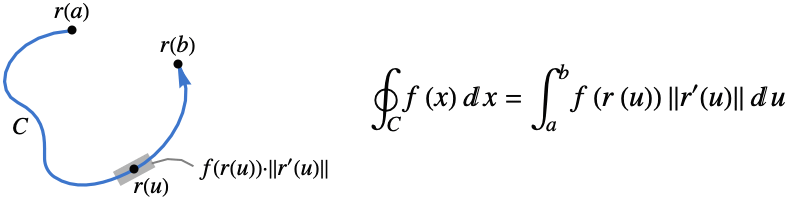
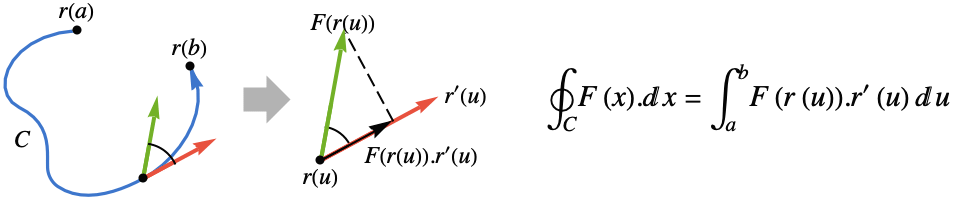
范例

打开所有单元关闭所有单元

基本范例 (7)

标量场在圆上的线积分：

矢量场在线段上的线积分：

矢量场在空间曲线上的线积分：

二维标量场的线积分：

要积分的曲线：

和曲线的等值线图：

线积分：

二维矢量场的线积分：

矢量场和积分路径：

线积分：

三维矢量场的线积分：

使用 VectorSymbol:

使用隐式向量符号：

范围 (32)

基本用法 (4)

标量场的线积分：

三维矢量场的线积分：

LineIntegrate 适用于许多特殊曲线：

参数曲线上的线积分：

标量函数 (11)

标量场在曲线上的线积分：

和曲线的等值线图：

线积分：

标量场在圆弧上的线积分：

标量场在参数曲线上的线积分：

函数和曲线的等值线图：

标量场在圆上的线积分：

标量场在空间曲线上的线积分：

线积分：

标量场在环形边界上的线积分：

函数和曲线的等值线图：

标量场在闭合多边形上的线积分：

函数和曲线的等值线图：

标量场在椭圆路径上的线积分：

函数和曲线的等高线图：

线积分：

标量场在参数曲线上的线积分：

线积分：

标量场在圆上的线积分：

和曲线的等值线图：

线积分：

标量场在圆盘扇区边界上的线积分：

和曲线的等值线图：

线积分：

矢量函数 (12)

三维矢量场在参数化曲线上的线积分：

矢量场和曲线的可视化：

线积分：

矢量场在二维曲线上的线积分：

线积分：

矢量场在圆弧上的线积分：

矢量场在线段上的线积分：

矢量场在三维参数化曲线上的线积分：

矢量场在曲线上的线积分：

矢量场在椭圆弧上的线积分：

矢量场在参数曲线上的线积分：

矢量场在三维参数曲线上的线积分：

矢量场在参数化曲线上的线积分：

矢量场在椭圆路径上的线积分：

高维矢量场的线积分：

特殊曲线 (4)

圆弧上的线积分：

矢量场在半径为 1 的圆扇形边界上的线积分：

多边形上的线积分：

环形边界上的线积分：

参数曲线 (1)

矢量场在三维螺旋上的线积分：

选项 (5)

Assumptions (1)

选项 Assumptions 可用于参数：

Direction (1)

闭合圆形路径的默认 Direction 是逆时针方向：

等价于：

可以使用选项 Direction 选择顺时针方向：

GenerateConditions (1)

LineIntegrate 可以使用符号参数：

抑制参数上的条件：

WorkingPrecision (2)

如果指定了 WorkingPrecision，则给出数值结果：

如果被积函数具有有限精度，则结果具有有限精度：

应用 (27)

大学微积分 (10)

函数在线段上的线积分：

矢量场在曲线上的线积分：

半径为 1 且线密度为的细圆线的质量：

力场对沿线段移动的粒子所做的功：

矢量场沿路径的线积分：

矢量场沿曲线的线积分：

当粒子沿曲线移动时，力所做的功：

矢量场沿以原点为中心的单位圆的线积分：

矢量场沿以原点为中心、半径为的圆的线积分：

矢量场在路径上线积分的数量值：

长度 (3)

圆的周长：

使用线积分计算心形周长：

长度也可以用 RegionMeasure 计算：

星形线的周长：

面积 (5)

使用线积分计算半轴为和的椭圆的面积：

使用线积分计算的双纽线右手环的面积：

参数为和的外摆线的面积：

使用线积分计算心形面积：

使用线积分计算星形线周长：

力所做的功 (4)

物体沿直线运动时，重力所做的功：

在电荷密度为的带电无限导线的电场中，当电荷从 {1,1,0} 移动到 {2,2,0}时，电力所做的功：

指向原点的弹力沿四分之一椭圆所做的功：

电荷在电荷的电场中沿轴从移动到无穷大时，电力所做的功：

质心 (2)

半径为且线密度为的闭合半圆导线的质量：

质心的坐标：

质心的坐标：

线密度恒定为的螺旋线的惯性矩：

关于轴：

关于轴：

关于轴：

经典定理 (3)

如果矢量场的线积分只取决于端点的值，而不取决于路径，那么这个矢量场为保守的（conservative）：

场是标量函数的梯度：

所有标量场的梯度都是保守的. 例如，在曲线上的线积分为：

这与曲线端点的值之差相同：

封闭曲线上矢量场的线积分为：

这与在曲线所包围区域内的曲面积分有关，其中的定义为：

向量场在三维空间中沿闭合直线的线积分为：

这等于以曲线为边界的任何曲面上的 Curl 的曲面积分：

相同边界的不同曲面的曲面积分是相同的：

属性和关系 (5)

如果符号计算失败，应用 N[LineIntegrate[...]] 获得数值解：

求单位线密度的三角形导线的质心：

求总质量：

求质心的分量：

也可以使用 RegionCentroid 获得质心：

求在 - 平面上以原点为中心的单位线密度圆线绕轴的惯性矩：

答案也可以用 MomentOfInertia 计算得到：

求外摆线的长度：

使用 ArcLength 可以获得相同的答案：

求椭圆的面积：

结果可以使用 RegionMeasure 获得：

巧妙范例 (2)

悬链线长度：

矢量场在 Clelia 曲线上的积分：

顶部