MatrixPlot
MatrixPlot[m]
绘制一个可视化描述矩阵中元素值的图形.
更多信息和选项

- 默认情况下,MatrixPlot[m] 向下纵向连续排列 m 行,将列横向连续排列,如同格式化普通的矩阵一样.
- 默认情况下,MatrixPlot 中 0 值显示为白色,而负值则是使用蓝色表示,正值用红色表示.
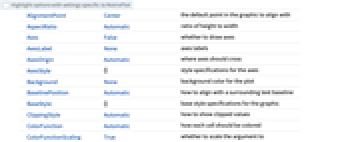
- MatrixPlot 具有同 ArrayPlot 相同的选项,并有以下改变: [所有选项的列表]
-
ClippingStyle Automatic 如何显示剪掉的值 Frame True 曲线周围是否绘制边框 FrameTicks All 边框中包含何种刻度 MaxPlotPoints Automatic 包含的点的最大值 - PlotRange->r 指出仅显示在 -r 和 +r 范围内的 aij.
- 默认设置 ColorFunctionScaling->True,缩放比例基于相对值和每个矩阵元素的阶. 最后尺度缩放后的值通常介于 0 和 1 之间,而尺度缩放后的值 0.5 对应于矩阵元素值 0.
- 默认设置 MaxPlotPoints->Automatic,对足够大或足够稀疏的矩阵取样,以便它们的结构可以在 MatrixPlot 生成的曲线中可见.
- MatrixPlot 可以同 SparseArray 对象一起使用.
所有选项的列表


范例
打开所有单元关闭所有单元范围 (19)
数据 (10)
演示 (9)
用一个自定义的颜色函数,该函数用蓝色表示负值,红色表示正值:
用 ColorRules 为不同的值上色:
用 ColorRules 和 ColorFunction 为元素上色, ColorRules 具有高优先级:
选项 (33)
Background (2)
ClippingStyle (3)
ColorFunction (5)
使用 ColorData 中一个指定的颜色梯度:
ColorFunctionScaling (4)
设置 ColorFunctionScaling->False,元素没有刻度:
设置 ColorFunctionScaling->False,MatrixPlot 同 ArrayPlot 一样执行:
ColorFunctionScaling 对 ColorRules 没有影响:
ColorRules (6)
在 ColorRules 中使用任何样式:
ColorRules 可以和 ColorFunction 连用,并有更高的优先级:
MaxPlotPoints (1)
PlotRange (3)
属性和关系 (6)
MatrixPlot 的颜色采用负值元素使用冷色,正值元素使用暖色:
ArrayPlot 使用灰度色标:
MatrixPlot 改变矩阵元素的比例用以区分大范围内的值:
用 ReliefPlot 处理医学和地理学数据:
用 ListDensityPlot,从连续的密度中为结构化或非结构化的数据取样:
用 ArrayPlot3D 绘制三维数据数组:
用 GraphPlot 观察邻接矩阵:
可能存在的问题 (2)
巧妙范例 (1)
在整数点处求 Sin 函数:
文本
Wolfram Research (2007),MatrixPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MatrixPlot.html (更新于 2014 年).
CMS
Wolfram 语言. 2007. "MatrixPlot." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/MatrixPlot.html.
APA
Wolfram 语言. (2007). MatrixPlot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MatrixPlot.html 年