MeshConnectivityGraph
MeshConnectivityGraph[mr,0]
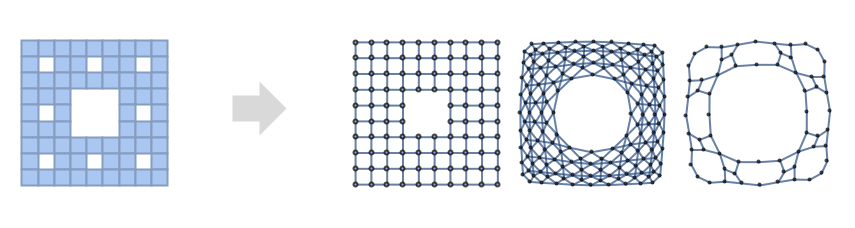
给出一张点图,其中的各个点由线相连.
MeshConnectivityGraph[mr,d]
给出维度为 d 的单元之间的图,各单元共享一个维度为 d-1 的单元.
MeshConnectivityGraph[mr,{d,e},r]
给出从维度为 d 的单元到维度为 e 的单元的图,它们共享一个维度为 r 的单元.
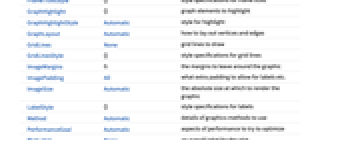
更多信息和选项


- MeshConnectivityGraph 亦称为网格邻接图和网格关联图.
- 常见用途包括获取网格中单元的邻接关系和拓扑信息.
- 连通图中的顶点 {d,i} 对应于单元 cd,i,其维度为 d,在网格 mr 中的索引为 i.
- 当单元 cd,i 和 cd,j 都有一个维度为 d-1 的公共子单元时,MeshConnectivityGraph[mr,d] 中的无向边就会连接两个顶点 {d,i} 和 {d,j}. 如果 d=0,公共子单元的维度为 1.
- d 的常见值为:
-
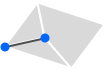
0 共享一条线的点 
1 共享一个点的线 
2 共享一条边的多边形 
3 共享一个多边形的多面体 - 在 MeshConnectivityGraph[mr,{d,e},r] 中,当单元 cd,i 和 ce,j 有一个维度为 r 的公共子单元(它是 cd,i 和 ce,j 的子集或超集)时,有向边将连接顶点 {d,i} 和顶点 {e,j}.
- MeshConnectivityGraph[mr] 实际上等价于 MeshConnectivityGraph[mr,0].
- MeshConnectivityGraph[mr,d,r]等价于图 MeshConnectivityGraph[mr,{d,d},r] 的无向图.
- MeshConnectivityGraph 采用与 Graph 相同的选项,但有以下不同之处:
-
AnnotationRules Inherited
所有选项的列表

范例
打开所有单元关闭所有单元基本范例 (2)
范围 (4)
MeshConnectivityGraph 适用于 MeshRegion:
MeshConnectivityGraph 适用于所有维度:
默认情况下,保留 AnnotationRulesInherited 的注释:
当设置为 AnnotationRulesNone 时,不保留注释,对图进行索引:
选项 (81)
AnnotationRules (4)
DirectedEdges (1)
用 DirectedEdges->False 将规则解释为无向边:
EdgeLabels (7)
将 Placed 与符号位置一起使用,以控制在边的什么位置放置标签:
通过 Tooltip 和 StatusArea 用值进行自动标注:
EdgeShapeFunction (6)
获取 EdgeShapeFunction 的内置设置列表:
EdgeShapeFunction 可与 EdgeStyle 组合使用:
EdgeShapeFunction 比 EdgeStyle 的优先级高:
GraphHighlightStyle (2)
GraphLayout (5)
VertexCoordinates 将覆盖 GraphLayout 的坐标:
用 AbsoluteOptions 提取用布局算法得出的 VertexCoordinates:
VertexCoordinates (2)
VertexLabels (13)
将 Placed 与符号式位置合用,控制标签的放置,包括顶点外的位置:
或 StatusArea:
VertexShape (5)
使用任意 Graphics、Image 或 Graphics3D 作为顶点的形状:
VertexShape 可与 VertexSize 组合使用:
VertexShape 不受 VertexStyle 的影响:
VertexShapeFunction 比 VertexShape 的优先级高:
VertexShapeFunction (10)
获取 VertexShapeFunction 的内置集合列表:
使用 "Basic" 集合中 VertexShapeFunction 的内置设置:
使用 "Rounded" 集合中 VertexShapeFunction 的内置设置:
使用 "Concave" 集合中 VertexShapeFunction 的内置设置:
VertexShapeFunction 可与 VertexStyle 组合使用:
VertexShapeFunction 比 VertexStyle 的优先级高:
VertexShapeFunction 可与 VertexSize 组合使用:
VertexShapeFunction 比 VertexShape 的优先级高:
VertexSize (8)
VertexSize 可与 VertexShapeFunction 组合使用:
VertexSize 可与 VertexShape 组合使用:
VertexStyle (5)
VertexShapeFunction 可与 VertexStyle 组合使用:
VertexShapeFunction 比 VertexStyle 的优先级高:
VertexStyle 可与 BaseStyle 组合使用:
VertexStyle 比 BaseStyle 的优先级高:
VertexShape 不受 VertexStyle 的影响:
应用 (10)
基本应用 (5)
多面体运算 (1)
拓扑运算 (3)
用 MeshConnectivityGraph 测试网格是否相连:
属性和关系 (3)
不同维度的单元之间的 MeshConnectivityGraph 是一个有向二分图:
相同维度的单元之间的网格连通图的 AdjacencyMatrix 是对称的:
文本
Wolfram Research (2020),MeshConnectivityGraph,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MeshConnectivityGraph.html.
CMS
Wolfram 语言. 2020. "MeshConnectivityGraph." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MeshConnectivityGraph.html.
APA
Wolfram 语言. (2020). MeshConnectivityGraph. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MeshConnectivityGraph.html 年