MinStableDistribution
MinStableDistribution[μ,σ,ξ]
表示定位参数为 μ、尺度参数为 σ 以及形状参数为 ξ 的广义最小极值分布.
更多信息

- MinStableDistribution 也称为 Fisher–Tippet 分布.
- 广义最小极值分布给出样本最小值的渐进分布,样本从正态、柯西或 β 等分布中抽取.
- 在广义最小极值分布中,当
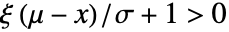 时,值
时,值 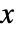 的概率密度与
的概率密度与 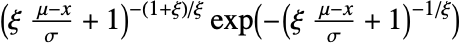 成正比,其余情况时为零.
成正比,其余情况时为零. - MinStableDistribution 允许 μ 和 ξ 为任意实数,σ 为任意正实数.
- MinStableDistribution 允许 μ 和 σ 为任意具有任意单位量纲的任意量,而 ξ 为无量纲量. »
- MinStableDistribution 可与 Mean、CDF 和 RandomVariate 等函数联合使用.
背景
- MinStableDistribution[μ,σ,ξ] 表示一个支持在满足
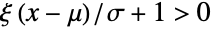 的实数
的实数 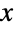 的集合上、由正实数 σ (尺度参数)及实数 μ 和 ξ (分别是位置参数和形状参数)参数化的连续统计分布. 这些参数共同作用决定分布的概率密度函数(PDF)的整体行为. 一般而言,尽管其整体形状(高度、伸展和最大值的水平位置)由 μ、 σ 和 ξ 的值决定,最小稳定分布的 PDF 是只有一个“顶点”(即全局最大值)的单峰的分布. 另外,PDF 的尾部是“薄”的,也就是说对较大的
的集合上、由正实数 σ (尺度参数)及实数 μ 和 ξ (分别是位置参数和形状参数)参数化的连续统计分布. 这些参数共同作用决定分布的概率密度函数(PDF)的整体行为. 一般而言,尽管其整体形状(高度、伸展和最大值的水平位置)由 μ、 σ 和 ξ 的值决定,最小稳定分布的 PDF 是只有一个“顶点”(即全局最大值)的单峰的分布. 另外,PDF 的尾部是“薄”的,也就是说对较大的 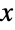 值而言,PDF呈指数而非代数降低. (这种行为可以通过分析分布的 SurvivalFunction 来获取定量的精确.)连同最大稳定分布(MaxStableDistribution),最小稳定分布是所谓的“极值分布”并可能被称作广义最小极值分布、1型极值分布(请注意不要与 ExtremeValueDistribution 混淆)、Gumbel 最小分部(请注意不要与 GumbelDistribution 混淆)和 Fisher-Tippet 分布.
值而言,PDF呈指数而非代数降低. (这种行为可以通过分析分布的 SurvivalFunction 来获取定量的精确.)连同最大稳定分布(MaxStableDistribution),最小稳定分布是所谓的“极值分布”并可能被称作广义最小极值分布、1型极值分布(请注意不要与 ExtremeValueDistribution 混淆)、Gumbel 最小分部(请注意不要与 GumbelDistribution 混淆)和 Fisher-Tippet 分布. - 广义最小极值分布是对从如 NormalDistribution、 CauchyDistribution 或 BetaDistribution 这样的分布中的一个样本的最小值的对称特性建模的独特分布,它也可以结合其他极值分布如 GumbelDistribution、 FrechetDistribution 和 WeibullDistribution 的行为. 由于其 PDF 是双指数的(也就是有 Exp[-Exp[…]] 的形式),分布的图像有更夸大的特性(如更高的顶点和更薄的尾部),这是分布中的一种独特的属性. 作为机制理论领域中的基础,最小稳定分布在描述“可能性极小”(比如数据集中包括与中位数有极端偏差的变量)的情况下有广泛的应用,并被用于对很多金融和经济的子领域中的现象建模.
- RandomVariate 可用于从最小稳定分布给出一个或多个机器精度或任意精度(后者通过 WorkingPrecision 选项)伪随机变量. Distributed[x,MinStableDistribution[μ,σ,ξ]],更简洁地写作 xMinStableDistribution[μ,σ,ξ],可用于断言变量 x 符合最小稳定分布. 这样的断言可用于如 Probability、 NProbability、 Expectation 和 NExpectation 等函数.
- 概率密度和累积分布函数可以通过 PDF[MinStableDistribution[μ,σ,ξ],x] 和 CDF[MinStableDistribution[μ,σ,ξ],x] 给出. 均值、中位数、方差、原始矩和中心距可以分别通过 Mean、 Median、 Variance、 Moment 和 CentralMoment 计算得出.
- DistributionFitTest 可用于测试一个给定数据集是否符合最小稳定分布, EstimatedDistribution 可用于从给定数据中估计最小稳定参数分布,而 FindDistributionParameters 可用于拟合数据至最小稳定分布. ProbabilityPlot 可用于生成给定数据的 CDF 对符号极值分布的 CDF 的图像,而 QuantilePlot 可用于生成给定数据的分位数对符号极值分布的分位数的图像.
- TransformedDistribution 可用于代表一个变形的极值分布, CensoredDistribution 可用于代表上限和下限值之间删节值的分布,而 TruncatedDistribution 可用于代表上限和下限之间的的截尾值的分布. CopulaDistribution 可用于构建含有最小稳定分布的更高维分布,而 ProductDistribution 可用于计算涉及极值分布的有独立组分分布的联合分布.
- 最小稳定分布与一些其他分布相关. MinStableDistribution 一般化包括 GumbelDistribution (GumbelDistribution[α,β] 同 MinStableDistribution[α,β,0] 相同)、 WeibullDistribution (WeibullDistribution[α,β] 同 MinStableDistribution[β,β/α,-1/α] 相同)和 ExpGammaDistribution (ExpGammaDistribution[1,σ,μ] 与 MinStableDistribution[μ,σ,0] 有相同的 PDF)在内的很多分布. 它可以通过变形获得如 MaxStableDistribution、 FrechetDistribution 和 ExtremeValueDistribution 的分布函数. MinStableDistribution 也与 ExponentialDistribution 和 LogisticDistribution 有关.
范例
打开所有单元关闭所有单元范围 (8)
偏度与 MaxStableDistribution 的偏度具有相反的符号:
峰度和 MaxStableDistribution 的峰度相同:
参数中保持一致地使用 Quantity 将给出 QuantityDistribution:
应用 (4)
MinStableDistribution 可以对年度最小平均日流量进行建模. 考虑马哈纳迪河流,以及以每秒立方米为单位给出的最小流量:
对数据进行 MinStableDistribution 拟合:
假设年度最小流量是独立的,求连续3年,最小流量不超过每秒2立方米的概率:
MinStableDistribution 可以用来对屈服强度建模:
把 MinStableDistribution 与数据拟合:
MinStableDistribution 可以用来对大小建模. 考虑直径为20微米的粉煤灰颗粒:
MinStableDistribution 可以用来对 Cyrtoideae radiolarians 放射虫长度建模:
属性和关系 (10)
当平移并且使用一个正因子为比例进行缩放时,新生成的分布仍然是 MinStableDistribution:
用负因子缩放会给出 MaxStableDistribution:
进行 Min 后 MinStableDistribution 是闭合的:
MinStableDistribution 的 CDF 求解稳定波动方程:
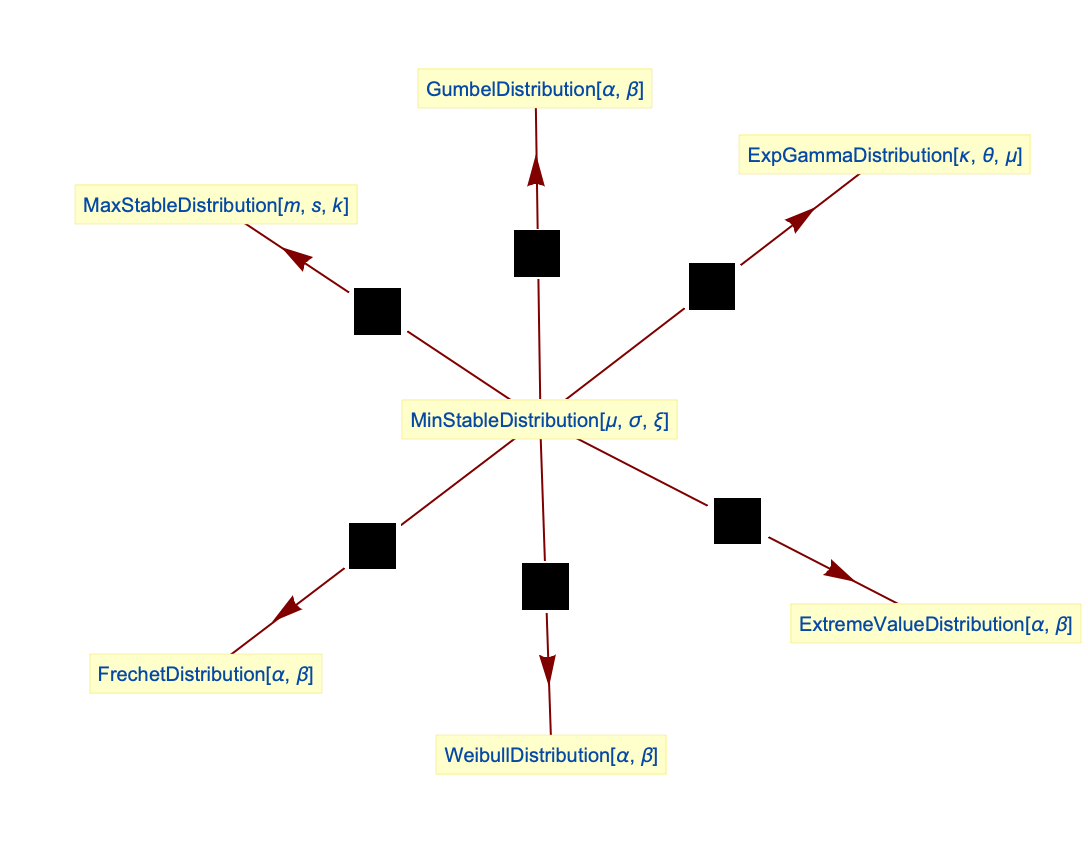
ExtremeValueDistribution 与一个广义最小极值分布相关:
GumbelDistribution 是广义最小极值分布的一个特例:
广义最小极值分布与 FrechetDistribution 相关:
WeibullDistribution 是广义最小极值分布的一个特例:
广义最小极值分布与 MaxStableDistribution 相关:
文本
Wolfram Research (2010),MinStableDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MinStableDistribution.html (更新于 2016 年).
CMS
Wolfram 语言. 2010. "MinStableDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/MinStableDistribution.html.
APA
Wolfram 语言. (2010). MinStableDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MinStableDistribution.html 年