MultinormalDistribution

MultinormalDistribution[Σ]

ゼロ平均，共分散行列 Σ の多変量正規分布を表す．

MultinormalDistribution[μ,Σ]

平均ベクトル μ，共分散行列 Σ の多変量正規（ガウス）分布を表す．

詳細

  • 多変量正規分布におけるベクトル 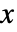の確率密度は 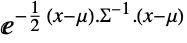に比例する．
  • MultinormalDistributionでは，μ は任意の実ベクトルでよく，Σ は 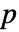×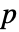（ただし，p=Length[μ]）の任意の正定値実数対称行列でよい．
  • 平均ベクトル μ と共分散行列 Σ は μ⊗μ と Σ が成分ごとに同じ単位次元であるような数量でよい， »
  • MultinormalDistributionは，Mean，CDF，RandomVariate等の関数とともに使うことができる．

予備知識

  • MultinormalDistribution[μ,Σ]は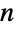， 個のタプル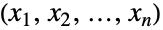すべての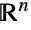の集合上でサポートされ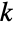， 番目の各（多変量）周辺分布が 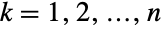についてNormalDistributionであるという特性によって特徴付けられる多変量連続統計分布を表す．言い換えるなら，変数の 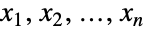のそれぞれが 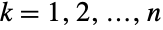について xkNormalDistributionを満足する．多変量正規分布MultinormalDistribution[μ,Σ]は，実数のベクトル μ および nLength[μ]Length[Σ]を満足し分布の陪平均，分散，共分散を定義する正定値対称行列 Σ でパラメータ化される．多変量正規分布の一変量周辺分布は正規分布に従う．
  • 多変量正規分布の確率密度関数(PDF)は単一の絶対最大値を持つが，二変量正規分布 (BinormalDistribution) のように，複数の「峰」（相対的極大値）を持つこともある．一般に，関連する周辺分布の各PDFの裾部は，周辺分布のPDFが 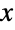の大きい値について代数的というよりもむしろ指数的に減少するという意味で「薄い」（この動作は周辺分布のSurvivalFunctionを分析することで数量的に厳密にすることができる）．
  • 多変量正規分布の応用の多くは，一般的な多変量正規分布の場合ではなく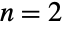，(BinormalDistribution)あるいは 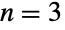の場合である．しかし，多変量中心極限定理の結果として，多変量正規分布を使って，値が指定された平均値の周りに集まっている任意の実数値確率変数集合を（少なくとも定性的に）説明することができる．正規分布の多変量バージョンについての初期の文献（中には1800年代にまで遡るものもある）は，主に二変量および三変量のケースに焦点を当てていた．これらはどちらも，遺伝学，材料科学，進化生物学，経済学，生態学，医学を含む幅広い分野に応用されている．
  • RandomVariateを使って，多変量正規分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,MultinormalDistribution[μ,Σ]] （より簡略な表記では xMultinormalDistribution[μ,Σ]）を使って，確率変数 x が多変量正規分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 確率密度関数および累積分布関数は，PDF[MultinormalDistribution[μ,Σ],x]およびCDF[MultinormalDistribution[μ,Σ],x]を使って得られる．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って，与えられたデータ集合が多変量正規分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからパラメトリック多変量正規分布を推定することが，FindDistributionParametersを使ってデータを多変量正規分布にフィットすることができる．ProbabilityPlotを使って記号多変量正規分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号多変量正規分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換された多変量正規分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使って多変量正規分布を含む高次元分布を構築することが，ProductDistributionを使って多変量正規分布を含む独立成分分布の結合分布を計算することができる．
  • MultinormalDistributionは，上述のように，NormalDistributionおよびBinormalDistributionを含む他の数多くの分布と関連している．MultinormalDistributionの一次元周辺分布はNormalDistributionに従うのに対し，各多変量周辺分布はMultinormalDistributionとなっている．MultinormalDistributionは，ν∞のときにPDF[MultinormalDistribution[{μ1,μ2},{{1,ρ},{ ρ,1}}],{x,y}]が厳密にPDF[MultivariateTDistribution[{μ1,μ2},{{1,ρ},{ ρ,1}},ν],{x,y}]の極限であるという意味で，MultivariateTDistributionの極限のケースである．さらに，MultinormalDistributionは変換(TransformedDistribution)によってLogMultinormalDistributionから得ることができる．MultinormalDistributionはRiceDistributionとも関係があり，一変量NormalDistributionとの関係から，LogNormalDistribution，DavisDistribution，LogLogisticDistribution，ExponentialDistribution，WeibullDistribution，GompertzMakehamDistribution，ExtremeValueDistribution，GammaDistributionとも関係がある．

例題

すべて開くすべて閉じる

例  (4)

確率密度関数：

累積分布関数：

平均と分散：

共分散：

スコープ  (8)

二変量正規分布から擬似乱数ベクトルのサンプルを生成する：

ヒストグラムを使ってサンプルを可視化する：

分布母数推定：

サンプルデータから分布母数を推定する：

適合度検定：

歪度と尖度は定数ベクトルである：

相関：

多変量正規分布の3D相関係数についてのImplicitRegion：

RandomPointを使って，3D相関係数領域上の一様分布からサンプルを抽出する：

ランダム相関行列の行列式が0.1未満である確率を推定する：

ハザード関数：

一変量周辺分布はNormalDistributionに従う：

多変量周辺分布は多変量正規分布に従う：

母数でQuantityを一貫して使うとQuantityDistributionが与えられる：

各測定量の標準偏差を求める：

一般化と拡張  (1)

MultinormalDistribution[Σ]は平均ゼロであると理解される：

アプリケーション  (2)

分布関数とそのヒストグラムを同じプロットで示す：

確率密度関数とそのヒストグラムを比較する：

累積分布関数とそのヒストグラムを比較する：

3つの突入電流の値についての多変量正規分布を4方向ノードに指定する：

ノードを出る電流の分布を求める：

電流値についての95%信頼区間を求める：

特性と関係  (10)

二変量正規分布の等確率の等高線：

多変量正規分布はアフィン変換の下では閉じている：

特定の値について：

他の分布との関係：

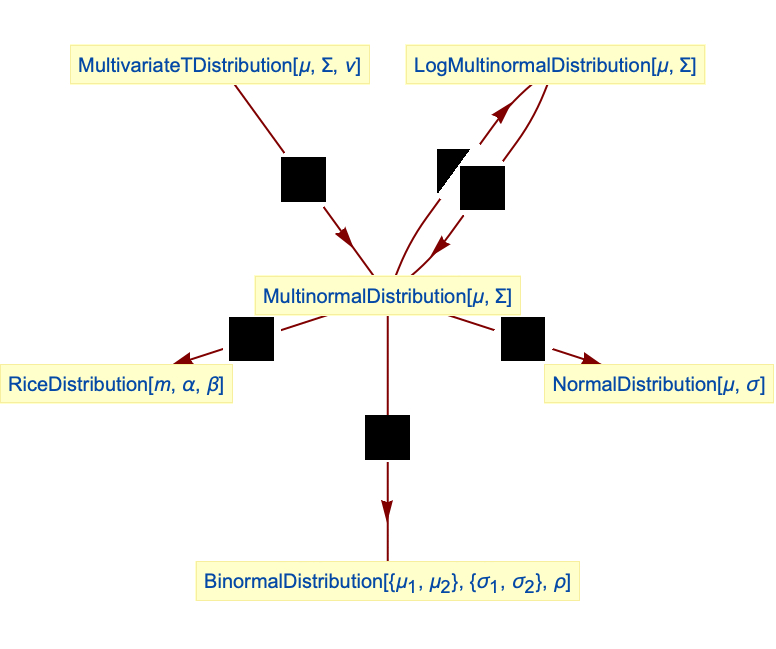
NormalDistributionは多変量正規分布の一変量のケースである：

BinormalDistributionは多変量正規分布の二次元のケースである：

多変量正規分布は が に近付く際のMultivariateTDistributionの極限である：

多変量正規分布はRiceDistributionに関連している：

LogMultinormalDistributionはMultinormalDistributionを変換したものである：

NormalDistributionはMultinormalDistributionから得ることができる：

MultinormalDistributionは，多変量正規カーネルとガウスの周辺分布を有するCopulaDistributionに等しい：

対応する多変量正規分布：

確率密度関数は等しい：

考えられる問題  (2)

μ が実ベクトルでなければMultinormalDistributionは定義されない：

μ と Σ の次元が一致していなければMultinormalDistributionは定義されない：

Σ が正定値対称行列ではない場合はMultinormalDistributionは定義されない：

無効な母数を記号出力に代入すると意味のない結果が返される：

Wolfram Research (2010), MultinormalDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/MultinormalDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2010), MultinormalDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/MultinormalDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2010. "MultinormalDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MultinormalDistribution.html.

APA

Wolfram Language. (2010). MultinormalDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MultinormalDistribution.html

BibTeX

@misc{reference.wolfram_2024_multinormaldistribution, author="Wolfram Research", title="{MultinormalDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MultinormalDistribution.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_multinormaldistribution, organization={Wolfram Research}, title={MultinormalDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/MultinormalDistribution.html}, note=[Accessed: 17-November-2024 ]}