MultivariateTDistribution

MultivariateTDistribution[Σ,ν]

represents the multivariate Student distribution with scale matrix Σ and degrees of freedom parameter ν.

MultivariateTDistribution[μ,Σ,ν]

represents the multivariate Student distribution with location μ, scale matrix Σ, and ν degrees of freedom.

Details

  • The probability density for vector 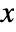in a multivariate 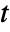distribution is proportional to 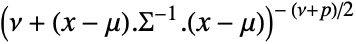, where 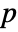is the length of .
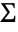  • The multivariate Student 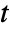distribution characterizes the ratio of a multinormal to the covariance between the variates.
  • MultivariateTDistribution allows Σ to be any 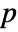× 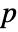symmetric positive definite matrix of real numbers, μ any vector of real numbers where p=Length[μ], and ν any positive real number.
  • The mean vector μ and covariance matrix Σ can be quantities such that μ⊗μ and Σ have the same unit dimensions componentwise, and ν can be a dimensionless quantity. »
  • MultivariateTDistribution can be used with such functions as Mean, CDF, and RandomVariate.

Background & Context

  • MultivariateTDistribution[μ,Σ,ν] represents a continuous multivariate statistical distribution supported over the set of 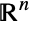of all 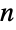-tuples 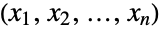characterized by the property that each of the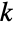 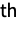^(th) (univariate) marginal distributions is StudentTDistribution for 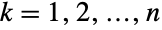. In other words, each of the variables 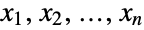satisfies xkStudentTDistribution for 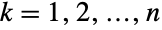. The multivariate 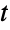-distribution is parametrized by a positive real number ν (indicating the degrees of freedom of the distribution), a vector μ of real numbers (called the "location" of the distribution), and a positive definite symmetric matrix Σ (called the "scale matrix"), which satisfy nLength[μ]Length[Σ] and which define the associated mean, variance, and covariance of the distribution. The two-argument version MultivariateTDistribution[Σ,ν] is equivalent to MultivariateTDistribution[{0,…,0},Σ,ν] and is sometimes referred to as the centered or centralized multivariate 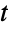-distribution.
  • The probability density function (PDF) of a multivariate 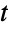-distribution has a single absolute maximum but may have multiple "peaks" (i.e. relative maxima). In general, the tails of each of the associated marginal PDFs are "fat" in the sense that the marginal PDF decreases algebraically rather than decreasing exponentially for large values of 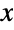. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of these marginal distributions.)
  • The multivariate 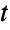-distribution characterizes the ratio of a multinormal to the covariance between the variates. Historically, a number of candidate distributions have been defined that have these same characteristics but are different than the one implemented here. The multivariate 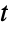-distribution defined above is a crucial tool in multivariate Bayesian analysis, arising in a number of contexts, including as the posterior distribution of the multinormal distribution and as the marginal posterior distribution of the regression coefficient vector in certain multivariate regression models. Because of this, the multivariate 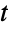-distribution is used in many applications related to Bayesian inference, as well as being a tool in a variety of contexts, including portfolio optimization, discriminant and cluster analysis, and multiple decision problems.
  • RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a multivariate 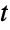-distribution. Distributed[x,MultivariateTDistribution[μ,Σ,ν]] , written more concisely as xMultivariateTDistribution[μ,Σ,ν], can be used to assert that a random variable x is distributed according to a multivariate 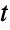-distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
  • The probability density and cumulative distribution functions for multivariate -distributions may be given using PDF[MultivariateTDistribution[μ,Σ,ν],{x1,x2,…,xn}] and CDF[MultivariateTDistribution[μ,Σ,ν],{x1,x2,…,xn}]. The mean, median, variance, covariance, raw moments, and central moments may be computed using Mean, Median, Variance, Covariance, Moment, and CentralMoment, respectively.
  • DistributionFitTest can be used to test if a given dataset is consistent with a multivariate 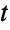-distribution, EstimatedDistribution to estimate a multivariate 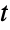-parametric distribution from given data, and FindDistributionParameters to fit data to a multivariate 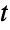-distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic multivariate 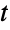-distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic multivariate 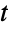-distribution.
  • TransformedDistribution can be used to represent a transformed multivariate 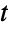-distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a multivariate 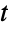-distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving multivariate -distributions.
  • MultivariateTDistribution is related to a number of other distributions. MultivariateTDistribution is connected to StudentTDistribution, as discussed above, and the one-dimensional marginals of a MultivariateTDistribution have a StudentTDistribution, while each of the multivariate marginals is again an instance of MultivariateTDistribution. MultivariateTDistribution limits to MultinormalDistribution in the sense that the limit of PDF[MultivariateTDistribution[{μ1,μ2},{{1,ρ},{ ρ,1}},ν],{x,y}] as ν∞ is precisely equivalent to PDF[MultinormalDistribution[{μ1,μ2},{{1,ρ},{ ρ,1}}],{x,y}] and, because of its relation to MultinormalDistribution, MultivariateTDistribution is related to LogMultinormalDistribution by way of TransformedDistribution. Because of its relation to the univariate StudentTDistribution, MultivariateTDistribution is also related to NoncentralStudentTDistribution, FRatioDistribution, NormalDistribution, HalfNormalDistribution, LogNormalDistribution, PearsonDistribution, CauchyDistribution, and ChiSquareDistribution.

Examples

open allclose all

Basic Examples  (4)

Probability density function:

Cumulative distribution function:

Mean and variance:

Covariance:

Scope  (9)

Generate a sample of pseudorandom vectors from a bivariate distribution:

Visualize the sample using a histogram:

Distribution parameters estimation:

Estimate the distribution parameters from sample data:

Goodness-of-fit test:

Skewness:

Skewness is always 0 when defined:

Kurtosis:

Kurtosis depends only on the degrees of freedom:

As the number of degrees of freedom approaches , the kurtosis approaches kurtosis of MultinormalDistribution:

Correlation for bivariate distribution:

Different mixed moments for a standard bivariate distribution:

Mixed central moments:

Mixed factorial moments:

Mixed cumulants:

Hazard function:

The marginals follow StudentTDistribution:

Consistent use of Quantity in parameters yields QuantityDistribution:

Applications  (3)

Show a distribution function and its histogram in the same plot:

Compare the PDF to its histogram version:

Compare the CDF to its histogram version:

A multivariate Student distribution is used to define a copula distribution:

Probability density function:

Mean and variance:

Generate random numbers:

Stock prices modeled with geometric Brownian motion are assumed to be normally distributed in their log returns. Here we examine this with stock prices of five companies, GOOG, MSFT, FB, AAPL, and INTC, in the year 2015:

Compute the log returns:

Fit the data to MultinormalDistribution and perform KolmogorovSmirnovTest:

Fit the data to MultivariateTDistribution and also perform the same test:

Properties & Relations  (6)

Equal probability contours for a bivariate distribution:

Multivariate Student distribution is closed under affine transformations:

The affine transformation need not preserve the distribution dimensionality:

Relationships to other distributions:

Multinormal distribution is the limit of MultivariateTDistribution as ν goes to :

The default location is 0:

MultivariateTDistribution is equivalent to CopulaDistribution with multivariate T kernel and Student marginals:

Possible Issues  (2)

MultivariateTDistribution is not defined when Σ is not a symmetric positive definite matrix:

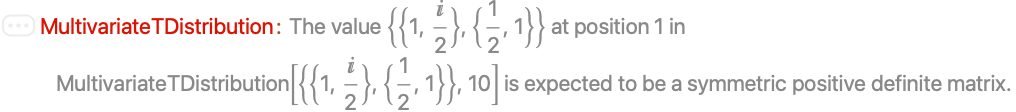
MultivariateTDistribution is not defined when ν is not positive:

Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:

Neat Examples  (1)

PDFs for different correlations:

Wolfram Research (2010), MultivariateTDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MultivariateTDistribution.html (updated 2016).

Text

Wolfram Research (2010), MultivariateTDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MultivariateTDistribution.html (updated 2016).

CMS

Wolfram Language. 2010. "MultivariateTDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MultivariateTDistribution.html.

APA

Wolfram Language. (2010). MultivariateTDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MultivariateTDistribution.html

BibTeX

@misc{reference.wolfram_2024_multivariatetdistribution, author="Wolfram Research", title="{MultivariateTDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MultivariateTDistribution.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_multivariatetdistribution, organization={Wolfram Research}, title={MultivariateTDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/MultivariateTDistribution.html}, note=[Accessed: 14-November-2024 ]}