NSurfaceIntegrate

NSurfaceIntegrate[f,{x,y,…}∈surface]

computes the numerical scalar surface integral of the function f[x,y,…] over the surface.

NSurfaceIntegrate[{p,q,…},{x,y,…}∈surface]

computes the numerical vector surface integral of the vector field {p[x,y,…],q[x,y,…],…}.

Details and Options

  • Surface integrals are also known as flux integrals.
  • Scalar surface integrals integrate scalar functions over a hypersurface. They are typically used to compute things like area, mass and charge for a surface.
  • Vector surface integrals are used to compute the flux of a vector function through a surface in the direction of its normal. Typical vector functions include a fluid velocity field, an electric field and a magnetic field.
  • The scalar surface integral of a function f over a surface 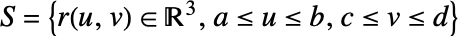is given by:
  • … where TemplateBox[{{{{partial, _, u}, {r, (, {u, ,, v}, )}}, x, {{partial, _, v}, {r, (, {u, ,, v}, )}}}}, Norm] is the measure of a parametric surface element.
  • The scalar surface integral of f over a hypersurface 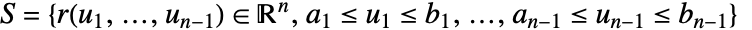is given by:

  • The scalar surface integral is independent of the parametrization and orientation of the surface. Any 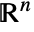dimensional RegionQ object in 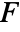can be use for the surface.
  • The vector surface integral of a vector function 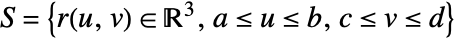over a surface 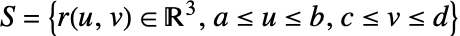is given by:
  • … where 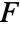F(r(u,v)).(partial_tr(u,v)xpartial_sr(u,v)) is the projection of the vector function 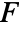onto the normal direction so only the component in the normal direction gets integrated.
  • The vector surface integral of 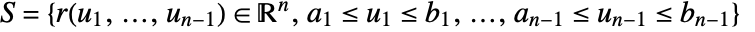over a a hypersurface 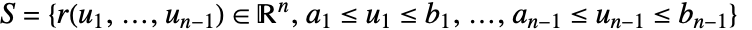is given by:

  • The vector surface integral is independent of the parametrization, but depends on the orientation.
  • The orientation for a hypersurface is given by a normal vector field 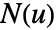over the surface.
  • For a parametric hypersurface ParametricRegion[{r1[u1,…,un-1],…,rn[u1,…,un-1]},…], the normal vector field 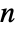is taken to be Cross[∂u1r[u],…,∂un-1r[u]].
  • The RegionQ objects in Wolfram Language are not oriented. However, for the convenience of this function, you can assume the following rules for getting oriented hypersurfaces.
  • For solid (of dimension 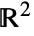) and bounded RegionQ objects ℛ, take the surface to be the region boundary (RegionBoundary[ℛ]) and the normal orientation to be pointed outward.
  • Special solids in with their assumed boundary surface (edge) normal orientations include:
  • Triangleoutward normal
    Rectangleoutward normal
    Polygonoutward normal
    Diskoutward normal
    Ellipsoidoutward normal
    Annulusoutward normal
  • Special solids in with their assumed boundary surface (face) normal orientations include:
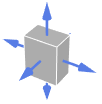
  • Tetrahedronoutward normal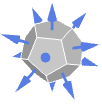
    Cuboidoutward normal
    Polyhedronoutward normal
    Balloutward normal
    Ellipsoidoutward normal
    Cylinderoutward normal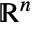
    Coneoutward normal
  • Special solids in with their assumed surface (facet) and normal orientations:
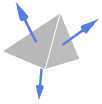
  • Simplexoutward normal
    Cuboidoutward normal
    Balloutward normal
    Ellipsoidoutward normal
  • The following options can be given:
  • AccuracyGoal Automaticdigits of absolute accuracy sought
    MaxPoints Automaticmaximum total number of sample points
    MaxRecursion Automaticmaximum number of recursive subdivisions
    Method Automaticmethod to use
    MinRecursion 0minimum number of recursive subdivisions
    PrecisionGoal Automaticdigits of precision sought
    WorkingPrecision Automaticthe precision used in internal computations

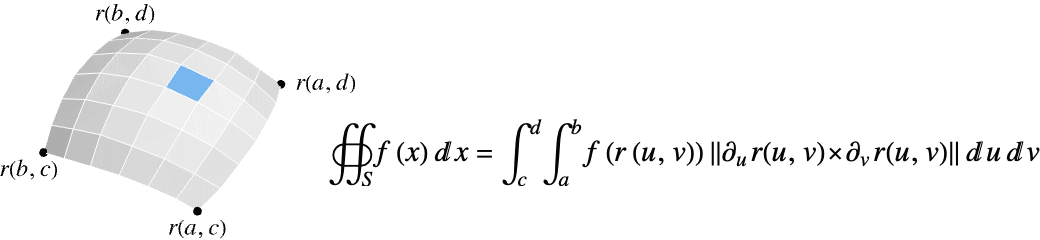
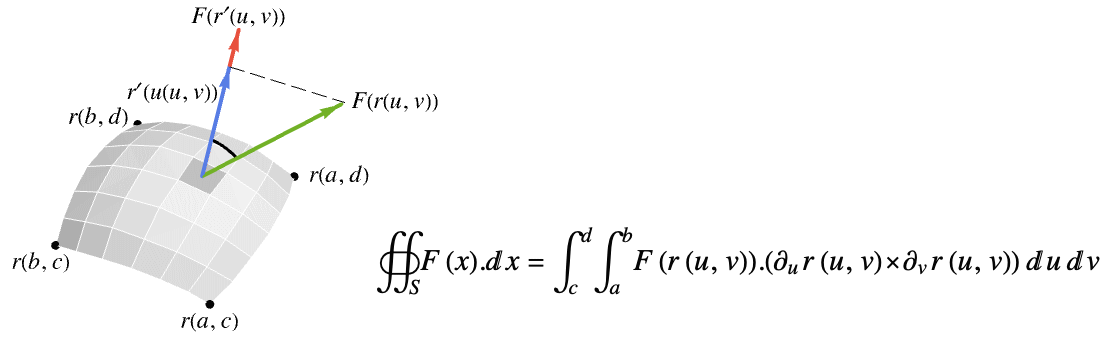
Examples

open allclose all

Basic Examples  (6)

Surface integral of a scalar function over a spherical surface:

Surface integral of a vector field over a spherical surface:

Surface integral of a scalar field over a parametric surface:

Surface integral of a vector field over a parametric surface:

Surface integral of a scalar field over a surface:

Visualize the scalar field on the surface:

Surface integral of a vector field over a surface:

Visualize the scalar field on the surface:

Scope  (32)

Basic Uses  (5)

Surface integral of a scalar field over a cube in three dimensions:

Surface integral of a vector field in three dimensions:

SurfaceIntegrate works with many special surfaces:

Surface integral over a parametric surface:

SurfaceIntegrate works in dimensions different from three:

Scalar Functions  (5)

Surface integral of a scalar field over a three-dimensional surface:

Plot of the surface:

Surface integral:

Surface integral of a scalar field over a triangle:

The surface integral:

Surface integral of a scalar field in three dimensions over a sphere:

Surface integral of a scalar field over the surface of a pyramid:

Surface integral:

Surface integral of a scalar field over a parametric surface in three dimensions:

The surface and its plot:

Vector Functions  (5)

Surface integral of a vector field in three dimensions over a sphere:

Visualize the vector field on the surface:

Surface integral:

Surface integral of a vector field in three dimensions over a triangle:

Surface integral:

Surface integral of a vector field over a parametric surface in three dimensions:

Surface integral of a vector field over the boundary of an ellipsoid:

Surface integral of a vector field in three dimensions over the boundary of a cone:

Visualization of the vector field on the surface:

Surface integral:

Special Surfaces  (10)

Surface integral of a vector field over a sphere of radius 1:

Surface integral of a vector field over the boundary of a cube of side 2 centered at the origin:

Surface integral of a vector field over the boundary of a tetrahedron:

Surface integral of a vector field over a triangle:

Surface integral of a vector field over an ellipsoid:

Surface integral of a vector field over the boundary of a cone:

Surface integral of a vector field over the boundary of a cylinder:

Surface integral of a vector field over the boundary of a parallelepiped:

Surface integral of a vector field over the boundary of a prism:

Surface integral over a polygon in three dimensions:

The orientation of the polygon depends on the order in which the points are given:

Parametric Surfaces  (4)

Surface integral of a vector field over a parametric surface:

Surface integral of a vector field over a parametrized dome-like surface:

Surface integral over a parametrized cylinder:

Surface integral of a vector field over a parametrized hyperboloid:

Hypersurfaces  (3)

Surface integral over a 1D hypersurface in 2D:

Surface integral over a 3D hypersurface in 4D:

Volume of a five-dimensional sphere, computed using a surface integral:

Options  (8)

AccuracyGoal  (1)

The option AccuracyGoal sets the number of digits of accuracy:

The result with default settings only sets a PrecisionGoal:

MaxPoints  (1)

The option MaxPoints stops the integration after a specified number of points has been evaluated:

With default options:

MaxRecursion  (1)

The option MaxRecursion specifies the maximum number of recursive steps:

Increasing the number of recursions:

Method  (1)

The option Method can take the same values as in NIntegrate. For example:

With default options:

MinRecursion  (1)

Useful for sharply peaked functions, the option MinRecursion forces a minimum number of subdivisions:

Compare to the exact result:

PrecisionGoal  (1)

The option PrecisionGoal sets the relative tolerance in the integration:

With default settings:

WorkingPrecision  (2)

If a WorkingPrecision is specified, the calculation is done with that working precision:

The integrand may have a finite precision:

Applications  (18)

College Calculus  (5)

Surface integral over the boundary of a cube of side 2 centered at the origin:

Surface integral over a paraboloid:

Surface integral over the side of a cylinder:

Surface integral over a hemispherical shell of radius 2:

Surface integral over the boundary of a cube:

Areas  (3)

Area of a sphere:

Area of an ellipsoid:

Area of a triangle:

Volumes  (3)

Volume of an ellipsoid computed using a surface integral:

Volume of an icosahedron computed using a surface integral:

Volume of a cube of side 3 computed using a surface integral:

Flux  (3)

Flux of the electric field generated by a point charge at the origin over a sphere surrounding it:

Flux of the uniform magnetic field of an infinite solenoid with windings per unit length traversed by a current over a disk orthogonal to it:

Electric field due to an infinite charged wire of linear charge density :

Flux across a cylinder of height and radius having the axis on the charged wire:

Centroids  (2)

Mass of a hemispherical shell of unit density and radius :

coordinate of the center of mass:

coordinate of the center of mass:

coordinate of the center of mass:

Moments of inertia of a thin cut cone:

About the axis:

About the axis:

About the axis:

Classical Theorems  (2)

Stokes's theorem. The surface integral of the Curl of a vector field :

The surface integral of over an open surface is:

It is the same as the line integral of over the boundary of the surface:

Divergence theorem. The surface integral of a vector field (with continuous partial derivatives) over a closed surface is:

It is the same as the integral of Div[f] over the interior of the surface:

Properties & Relations  (5)

Apply N[SurfaceIntegrate[…]] to obtain a numerical solution with NSurfaceIntegrate if the symbolic calculation fails:

Find the center of mass of a thin triangular surface of unit mass per unit area:

Find the total mass:

Find the component of the center of mass:

Find the component of the center of mass:

Find the component of the center of mass:

The center of mass can also be obtained using RegionCentroid:

Find the moment of inertia around the axis of a thin cylindrical shell of unit area density:

The answer can also be computed with MomentOfInertia:

Find the area of a tetrahedron:

The answer can also be computed with SurfaceArea:

Find the volume of an icosahedron:

The answer can also be computed with Volume:

Neat Examples  (9)

Volume of a pseudosphere computed using a surface integral:

Plot of a finite part of the pseudosphere:

Volume of a drop-shaped solid using a surface integral:

Volume of a Dupin cyclide:

Flux of a vector field across a part of a Bohemian dome:

Surface integral of a vector field over a portion of a conocuneus of Wallis:

Surface integral of a vector field over a funnel-shaped surface:

Area of a Gaudi surface:

Compute numerically the area of Guimard's surface:

Surface integral of a vector field over a Neiloid:

Wolfram Research (2024), NSurfaceIntegrate, Wolfram Language function, https://reference.wolfram.com/language/ref/NSurfaceIntegrate.html.

Text

Wolfram Research (2024), NSurfaceIntegrate, Wolfram Language function, https://reference.wolfram.com/language/ref/NSurfaceIntegrate.html.

CMS

Wolfram Language. 2024. "NSurfaceIntegrate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NSurfaceIntegrate.html.

APA

Wolfram Language. (2024). NSurfaceIntegrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NSurfaceIntegrate.html

BibTeX

@misc{reference.wolfram_2024_nsurfaceintegrate, author="Wolfram Research", title="{NSurfaceIntegrate}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/NSurfaceIntegrate.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_nsurfaceintegrate, organization={Wolfram Research}, title={NSurfaceIntegrate}, year={2024}, url={https://reference.wolfram.com/language/ref/NSurfaceIntegrate.html}, note=[Accessed: 05-November-2024 ]}