NoncentralFRatioDistribution
NoncentralFRatioDistribution[n,m,λ]
分子の自由度 n,分母の自由度 m で,分子の非心母数が λ である非心F分布を表す.
NoncentralFRatioDistribution[n,m,λ, η]
分子の非心母数が λ,分母の非心母数が η の二重非心F分布を表す.
詳細

- 非心F分布は,非心カイ二乗(
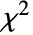 )確率変数とカイ二乗(
)確率変数とカイ二乗(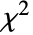 )確率変数をそれぞれの自由度で割ったものの比の分布である.
)確率変数をそれぞれの自由度で割ったものの比の分布である. - 二重非心F分布は非心カイ分布に従うそれぞれの自由度で割られた2つの確率変数の比の分布である.
- NoncentralFRatioDistributionでは,n および m は任意の正の実数,λ および η は任意の非負の実数でよい.
- NoncentralFRatioDistributionでは,n,m,λ,η は無次元量でよい.
- NoncentralFRatioDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる.
予備知識
- NoncentralFRatioDistribution[n,m,λ,η]は,区間
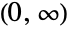 上でサポートされ,比
上でサポートされ,比 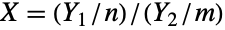 の分布として定義された連続統計分布を表す.ただし,Y1NoncentralChiSquareDistribution[n,λ]とY2NoncentralChiSquareDistribution[m,η]は,自由度 n および m,非心母数 λ および η をそれぞれ持つ独立変数である.確率密度関数(PDF)は,n,m,λ,η の値によって,単峰性か潜在的特異値が領域の下限に近付く単調減少のどちらかになる.さらに,PDFの裾部は,PDFが
の分布として定義された連続統計分布を表す.ただし,Y1NoncentralChiSquareDistribution[n,λ]とY2NoncentralChiSquareDistribution[m,η]は,自由度 n および m,非心母数 λ および η をそれぞれ持つ独立変数である.確率密度関数(PDF)は,n,m,λ,η の値によって,単峰性か潜在的特異値が領域の下限に近付く単調減少のどちらかになる.さらに,PDFの裾部は,PDFが 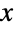 の大きい値について指数的というよりもむしろ代数的に現象するという意味で「太い」(この動作は分布のSurvivalFunctionを分析することで数量的に厳密にできる).4引数の形のNoncentralFRatioDistribution[n,m,λ,η]が一般に二重非心F分布と呼ばれるのに対し,3引数の形のNoncentralFRatioDistribution[n,m,λ](これが一般に非心F分布と呼ばれるものである)はNoncentralFRatioDistribution[n,m,λ,λ]に等しく,非心Fisher–Snedeco分布あるいはSnedecorの非心F分布と呼ばれることがある.
の大きい値について指数的というよりもむしろ代数的に現象するという意味で「太い」(この動作は分布のSurvivalFunctionを分析することで数量的に厳密にできる).4引数の形のNoncentralFRatioDistribution[n,m,λ,η]が一般に二重非心F分布と呼ばれるのに対し,3引数の形のNoncentralFRatioDistribution[n,m,λ](これが一般に非心F分布と呼ばれるものである)はNoncentralFRatioDistribution[n,m,λ,λ]に等しく,非心Fisher–Snedeco分布あるいはSnedecorの非心F分布と呼ばれることがある. - 非心F分布は1930年代の終りにはじめて導出されたが,その特性は1940年代の終りのPatnaikの著作までほとんど研究されなかった.Patnaikによって名付けられた非心F分布は,いわゆる非標準的な条件下の分散検定の分析における特性の研究に使われてきており,それ自身が,コンピュータサイエンス,数値解析,近似理論等の分野における研究の触媒となっている.この分布の最もよく知られた応用の多くは統計学におけるもので,この分野で,(例えばホテリング
 検定に基づく検定等で)中心F統計に基づく検定の力を計算するため等に使われている.非心F分布は,多重使用信頼推定による多変量較正問題の研究にも使われている.
検定に基づく検定等で)中心F統計に基づく検定の力を計算するため等に使われている.非心F分布は,多重使用信頼推定による多変量較正問題の研究にも使われている. - RandomVariateを使って,非心F分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,NoncentralFRatioDistribution[n,m,λ,η]](より簡略な表記では xNoncentralFRatioDistribution[n,m,λ,η])を使って,確率変数 x が非心F分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[NoncentralFRatioDistribution[n,m,λ,η],x]およびCDF[NoncentralFRatioDistribution[n,m,λ,η],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合が非心F分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリック非心F分布を推定することが,FindDistributionParametersを使ってデータを非心F分布にフィットすることができる.ProbabilityPlotを使って記号非心F分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号非心F分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された非心F分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って非心F分布を含む高次元分布を構築することが,ProductDistributionを使って非心F分布を含む独立成分分布の結合分布を計算することができる.
- NoncentralFRatioDistributionは他の多くの分布と関連がある.これは,NoncentralFRatioDistribution[n,m,0,0]とNoncentralFRatioDistribution[n,m,0]両方のPDFが厳密にFRatioDistribution[n,m]のPDFと等しいという意味で,FRatioDistributionを直接一般化したものである.NoncentralFRatioDistributionはNoncentralChiSquareDistributionとNoncentralBetaDistribution両方の変換(TransformedDistribution)として実現することができ,ChiDistribution,ChiSquareDistribution.StudentTDistribution,LaplaceDistribution,FisherZDistributionとも密接な関係がある.
例題
すべて開くすべて閉じるアプリケーション (1)
NoncentralFRatioDistributionは線形モデルフィットの係数についての仮説検定のベキ関数の計算に現れる.次の21個のサンプル点が実験で測定された:
特定の値を同時に持つ係数 ![]() と
と ![]() についての仮説検定はFRatioDistributionに従うそれぞれ自由度が2と9の
についての仮説検定はFRatioDistributionに従うそれぞれ自由度が2と9の ![]() 統計を使って行われた:
統計を使って行われた:
真の値が実際には1.37と2.88であると仮定すると,![]() 統計は非心母数
統計は非心母数 ![]() でNoncentralFRatioDistributionに従うことになる:
でNoncentralFRatioDistributionに従うことになる:
特性と関係 (6)
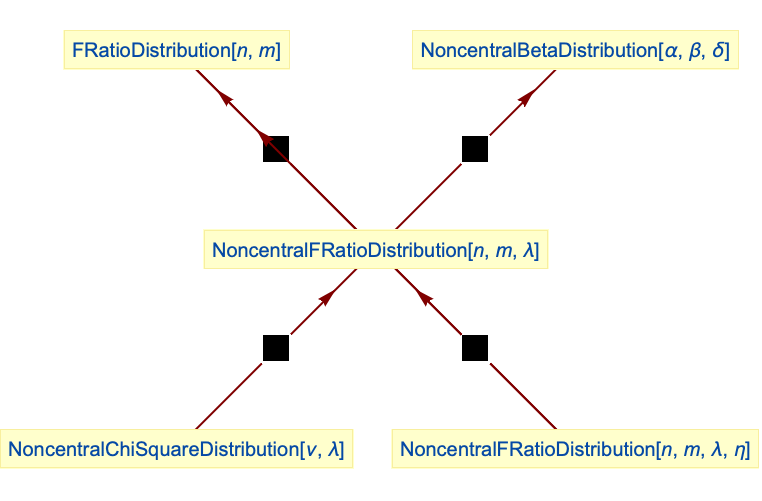
非心F分布を簡約するとFRatioDistributionになる:
二重非心F分布を簡約するとFRatioDistributionになる:
2つのNoncentralChiSquareDistributionの比は非心F分布に従う:
NoncentralBetaDistributionはNoncentralFRatioDistributionを変換したものである:
考えられる問題 (4)
NoncentralFRatioDistributionは,n あるいは m が正の実数でないときは定義されない:
NoncentralFRatioDistributionは,λ が非負の実数でないときは定義されない:
テキスト
Wolfram Research (2007), NoncentralFRatioDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/NoncentralFRatioDistribution.html (2016年に更新).
CMS
Wolfram Language. 2007. "NoncentralFRatioDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/NoncentralFRatioDistribution.html.
APA
Wolfram Language. (2007). NoncentralFRatioDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NoncentralFRatioDistribution.html