FisherZDistribution
✖
FisherZDistribution[n,m]
represents a Fisher 
distribution with n numerator and m denominator degrees of freedom.
Details
- The probability density for value
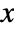in a Fisher 
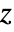distribution is proportional to 
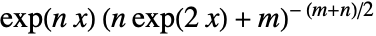for all real 
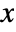. - FisherZDistribution allows n and m to be any positive real numbers.
- FisherZDistribution allows n and m to be dimensionless quantities.
- FisherZDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- FisherZDistribution[n,m] represents a continuous statistical distribution defined over the set of real numbers and parameterized by two positive real numbers n and m that represent degrees of freedom. The probability density function (PDF) of the Fisher
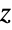distribution is smooth and unimodal, and the parameters m and n determine its overall height and steepness. In addition, the tails of the PDF are "thin", in the sense that the PDF decreases exponentially for large values of 
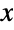. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) - Fisher's
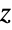distribution is obtained as the distribution of the random variable 
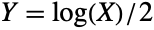, where XFRatioDistribution, and was first presented in the mid-1920s by English statistician Ronald Fisher. Fisher's 
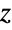distribution was devised as a tool for analyzing the errors of widely used distributions of the time and can be utilized in many of the same applications as FRatioDistribution. However, because FRatioDistribution is mathematically simpler, it has become somewhat uncommon to use FisherZDistribution to model real-world scenarios, though one example in which FisherZDistribution is preferable is in modeling the so-called 
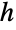-statistic among variates that are binormally (BinormalDistribution) distributed. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from Fisher's
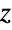distribution. Distributed[x,FisherZDistribution[n,m]], written more concisely as xFisherZDistribution[n,m], can be used to assert that a random variable x is distributed according to Fisher's 
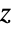distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation. - The probability density and cumulative distribution functions may be given using PDF[FisherZDistribution[n,m],x] and CDF[FisherZDistribution[n,m],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with Fisher's
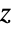distribution, EstimatedDistribution to estimate a Fisher's 
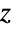parametric distribution from given data, and FindDistributionParameters to fit data to a Fisher's 
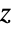distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Fisher's 
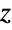distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Fisher's 
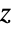distribution - TransformedDistribution can be used to represent a transformed Fisher's
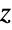distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Fisher's 
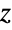distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Fisher's 
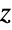distributions. - Fisher's
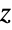distribution is related to a number of other distributions. As previously noted, FisherZDistribution is obtained as a transformation of FRatioDistribution, so that the PDF of FisherZDistribution[n,m] is precisely the same as that of TransformedDistribution[Log[u]/2,u FRatioDistribution[n,m]]. FisherZDistribution approaches normality, in the sense that FisherZDistribution[n,m] approaches NormalDistribution[μ,σ] as m and n tend to Infinity for 
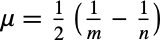and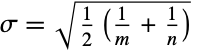 
. Finally, ChiSquareDistribution and StudentTDistribution can be derived as transformations of FisherZDistribution. FisherZDistribution is also related to ParetoDistribution, BinormalDistribution, and LogNormalDistribution.
Examples
open allclose allBasic Examples (4)Summary of the most common use cases
In[1]:=1
✖
https://wolfram.com/xid/0cf115pssxk9v9m-f430fi
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf115pssxk9v9m-tsfu9z
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf115pssxk9v9m-ji5qm5
Out[3]=3
Cumulative distribution function:
In[1]:=1
✖
https://wolfram.com/xid/0cf115pssxk9v9m-xxw4vl
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf115pssxk9v9m-gqha2n
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf115pssxk9v9m-mzhr9i
Out[3]=3
In[1]:=1
✖
https://wolfram.com/xid/0cf115pssxk9v9m-0qomc9
Out[1]=1
In[1]:=1
✖
https://wolfram.com/xid/0cf115pssxk9v9m-by6hml
Out[1]=1
Scope (7)Survey of the scope of standard use cases
Generate a sample of pseudorandom numbers from a Fisher 
distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf115pssxk9v9m-qhtk5j
Compare its histogram to the PDF:
In[2]:=2
✖
https://wolfram.com/xid/0cf115pssxk9v9m-03mwaz
Out[2]=2
Distribution parameters estimation:
In[1]:=1
✖
https://wolfram.com/xid/0cf115pssxk9v9m-45b7g2
Estimate the distribution parameters from sample data:
In[2]:=2
✖
https://wolfram.com/xid/0cf115pssxk9v9m-epi747
Out[2]=2
Compare the density histogram of the sample with the PDF of the estimated distribution:
In[3]:=3
✖
https://wolfram.com/xid/0cf115pssxk9v9m-f8ui5o
Out[3]=3
In[1]:=1
✖
https://wolfram.com/xid/0cf115pssxk9v9m-q8e19n
Out[1]=1
In[1]:=1
✖
https://wolfram.com/xid/0cf115pssxk9v9m-qk8skd
Out[1]=1
Different moments with closed forms as functions of parameters, including Moment:
In[1]:=1
✖
https://wolfram.com/xid/0cf115pssxk9v9m-hmd9kf
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf115pssxk9v9m-ejyy2n
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf115pssxk9v9m-cfua13
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0cf115pssxk9v9m-fqq16
Out[4]=4
In[1]:=1
✖
https://wolfram.com/xid/0cf115pssxk9v9m-zf22f9
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf115pssxk9v9m-ihao78
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf115pssxk9v9m-ofi6by
Out[3]=3
In[1]:=1
✖
https://wolfram.com/xid/0cf115pssxk9v9m-49opmm
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf115pssxk9v9m-bfy9g7
Out[2]=2
Applications (1)Sample problems that can be solved with this function
Given a binormal sample, the 
-statistic follows a shifted FisherZDistribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf115pssxk9v9m-bk3ozc
Generate the distribution of 
-statistics for binormal samples of size 
:
In[2]:=2
✖
https://wolfram.com/xid/0cf115pssxk9v9m-ymv37y
Visually compare the 
-statistic distribution to a shifted FisherZDistribution:
In[3]:=3
✖
https://wolfram.com/xid/0cf115pssxk9v9m-kpife8
In[4]:=4
✖
https://wolfram.com/xid/0cf115pssxk9v9m-v4c9wl
Out[4]=4
DistributionFitTest confirms the result:
In[5]:=5
✖
https://wolfram.com/xid/0cf115pssxk9v9m-br4qvj
Out[5]=5
Properties & Relations (2)Properties of the function, and connections to other functions
Relationships to other distributions:
Fisher 
distribution is a transformation of FRatioDistribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf115pssxk9v9m-h7vi5g
Out[1]=1
Wolfram Research (2010), FisherZDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/FisherZDistribution.html (updated 2016).
✖
Wolfram Research (2010), FisherZDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/FisherZDistribution.html (updated 2016).Text
Wolfram Research (2010), FisherZDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/FisherZDistribution.html (updated 2016).
✖
Wolfram Research (2010), FisherZDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/FisherZDistribution.html (updated 2016).CMS
Wolfram Language. 2010. "FisherZDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/FisherZDistribution.html.
✖
Wolfram Language. 2010. "FisherZDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/FisherZDistribution.html.APA
Wolfram Language. (2010). FisherZDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FisherZDistribution.html
✖
Wolfram Language. (2010). FisherZDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FisherZDistribution.htmlBibTeX
✖
@misc{reference.wolfram_2025_fisherzdistribution, author="Wolfram Research", title="{FisherZDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/FisherZDistribution.html}", note=[Accessed: 26-March-2025
]}BibLaTeX
✖
@online{reference.wolfram_2025_fisherzdistribution, organization={Wolfram Research}, title={FisherZDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/FisherZDistribution.html}, note=[Accessed: 26-March-2025
]}