

Product 
詳細とオプション


- Product[f,{i,imax}]は
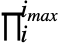 f と入力できる.
f と入力できる. - ∏は
 prod
prod または\[Product]と入力できる.
または\[Product]と入力できる. - Product[f,{i,imin,imax}]は
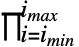 f と入力できる.
f と入力できる. - 極限は,通常の入力では∏の真下付き文字と真上付き文字で,他のテキストに入れ込まれる場合は下付き文字と上付き文字で表される.
- Productは,Wolfram言語の標準的な反復の指定を使用する.
- 反復変数 i は,実質的にBlockを使って局所的なものとして取り扱われる.
- 乗積範囲が有限の場合,一般に i には一連の値が割り当てられ,そのそれぞれについて f が評価される.
- 多乗積では,最も外側の変数の範囲がまず与えられる.
- 乗積の極限は数値である必要はなく,Infinityあるいは記号式でもよい.
- 乗積が有限個の項で乗ずることにより具体的に実行できない場合,Productは記号的な結果を求めることを試みる.この際,f が初めに記号的に評価される.
- 不定形の積
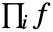 は連続する
は連続する 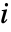 を持つ項の割合が
を持つ項の割合が 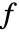 を返すと定義できる.
を返すと定義できる. - 定和分と不定和分はどのような順序ででも混ぜることができる.
- 次は,使用可能なオプションである.
-
Assumptions $Assumptions パラメータについての仮定 GenerateConditions False パラメータについての条件を含む答を生成するかどうか GeneratedParameters None 生成されたパラメータにどのように名前を付けるか Method Automatic 使用するメソッド Regularization None 使用する正規化 VerifyConvergence True 収束を確かめるかどうか - Regularizationの可能な値にはNoneと"Dirichlet"がある.{reg1,reg2,…}は多重積において異なるスキームに異なる変数を指定する.
- Productは標準的な本の公式集に載っているすべての基礎的な乗積を行うことができる.
- Productは∏を使ってStandardFormで出力される.
- Parallelize[Product[f,iter]]またはParallelProduct[f,iter]はProduct[f,iter]をすべてのサブカーネルで並列に計算する. »
例題
すべて開く すべて閉じるスコープ (28)
基本的な用法 (9)
最も外側の積の境界は,より内側の変数に依存することができる:
GenerateConditionsを使って答が真となる条件を求める:
結果の答をRefineする:
Assumptionsを使ってProductに仮定を直接与える:
特殊な不定形の積 (10)
超幾何項数列はBarnesGを使って表すことができる:
DiscreteRatioはすべての超幾何項数列について有理である:
一般にこれらの積にはBarnesGが必要である:
q有理関数の積は常にq有理関数とq階乗関数によって得ることができる:
一般にRootオブジェクトが必要である:
特殊積 (9)
一般化と拡張 (1)
ParallelProductはProductを並列に計算する:
Productは,事実上ParallelProductを使って自動的に並列化できる:
オプション (4)
アプリケーション (6)
ラグランジュ補間を使った近似表示 (1)
パラメータ推定のための尤度関数 (1)
小さいデータ集合のExponentialDistributionについての尤度関数:
BernoulliDistributionの尤度関数:
特性と関係 (4)
考えられる問題 (2)
テクニカルノート
-
▪
- 和と積 ▪
- 実装に関するノート: 代数と解析
履歴
1988 で導入 (1.0) | 1996 で更新 (3.0) ▪ 2008 (7.0) ▪ 2019 (12.0)
テキスト
Wolfram Research (1988), Product, Wolfram言語関数, https://reference.wolfram.com/language/ref/Product.html (2019年に更新).
CMS
Wolfram Language. 1988. "Product." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Product.html.
APA
Wolfram Language. (1988). Product. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Product.html
BibTeX
@misc{reference.wolfram_2025_product, author="Wolfram Research", title="{Product}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Product.html}", note=[Accessed: 17-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_product, organization={Wolfram Research}, title={Product}, year={2019}, url={https://reference.wolfram.com/language/ref/Product.html}, note=[Accessed: 17-February-2026]}