

Product 
更多信息和选项


- Product[f,{i,imax}] 可以输出为
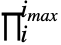 f.
f. - ∏ 可以输出为
 prod
prod 或 \[Product].
或 \[Product]. - Product[f,{i,imin,imax}] 可以输出为
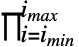 f.
f. - 在正常输出中,∏ 的限应为底标和顶标,而当嵌在其它文本中时为下标和上标.
- Product 用标准的 Wolfram 语言迭代指定.
- 迭代变量 i 通过使用 Block 视为局部的.
- 如果一个乘积范围是有限的,i 通常分配给一系列值,每个值计算 f.
- 在多重积中,首先给出最外层变量的范围.
- 一个乘积的极限不一定是数. 它们可以是 Infinity 或符号表达式.
- 如果一个乘积不能表示成有限项的乘积形式,Product 试图找到一个符号结果. 在这种情况下,f 首先进行符号计算.
- 定义了不定乘积
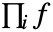 ,以便有连续
,以便有连续 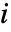 的项的比率给出
的项的比率给出 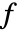 .
. - 定和不定总和可以以任何顺序混合使用.
- 可以提供以下选项:
-
Assumptions $Assumptions 关于参数的假设 GenerateConditions False 是否产生涉及参数条件的答案 GeneratedParameters None 如何命名产生的参数 Method Automatic 使用的方法 Regularization None 使用哪种正规化 VerifyConvergence True 是否验证收敛性 - Regularization 的可能值包括 None 和 "Dirichlet". {reg1,reg2,…} 在多重积中,对不同的变量指定不同的方案.
- Product 实际上执行标准表给出的所有乘积.
- Product 用 ∏ 以 StandardForm 形式输出.
- Parallelize[Product[f,iter]] 或 ParallelProduct[f,iter] 在所有子内核中并行计算 Product[f,iter]. »
范例
打开所有单元 关闭所有单元范围 (28)
基本用途 (9)
特殊不定乘积 (10)
超几何项序列可以用 BarnesG 来表达:
对所有超几何项序列, DiscreteRatio 是有理数:
它们的乘积一般需要 BarnesG:
q 有理函数的乘积总是可以用 q 有理数和 q 阶乘来表示:
一般需要 Root 对象:
特殊有限乘积 (9)
超几何项的乘积可以用 BarnesG 来表达:
推广和延伸 (1)
ParallelProduct 并行计算 Product:
Product 可以有效使用 ParallelProduct 自动并行运行:
选项 (4)
应用 (6)
乘积定义的函数 (1)
估计参数的似然函数 (1)
属性和关系 (4)
可能存在的问题 (2)
技术笔记
历史
1988年引入 (1.0) | 在以下年份被更新:1996 (3.0) ▪ 2008 (7.0) ▪ 2019 (12.0)
文本
Wolfram Research (1988),Product,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Product.html (更新于 2019 年).
CMS
Wolfram 语言. 1988. "Product." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2019. https://reference.wolfram.com/language/ref/Product.html.
APA
Wolfram 语言. (1988). Product. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Product.html 年
BibTeX
@misc{reference.wolfram_2025_product, author="Wolfram Research", title="{Product}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Product.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_product, organization={Wolfram Research}, title={Product}, year={2019}, url={https://reference.wolfram.com/language/ref/Product.html}, note=[Accessed: 03-March-2026]}