ProductDistribution
ProductDistribution[dist1,dist2,…]
独立した成分分布 dist1, dist2, …の結合分布を表す.
詳細
- ProductDistribution[dist1,dist2,…]の確率密度は
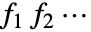 で与えられる.ただし,
で与えられる.ただし,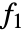 は dist1の確率密度,
は dist1の確率密度,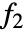 は dist2の確率密度(以下同様)である.
は dist2の確率密度(以下同様)である. - {disti,n}という表記は distiが n 回繰り返されることを表す.
- 分布 disti は一変量分布,多変量分布,連続分布,離散分布の任意の結合でよい.
- ProductDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- ProductDistribution[dist1,dist2,…,distn]は,第
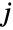 周辺分布(MarginalDistribution)が厳密に distjであり,成分分布 dist1,dist2,…,distnが独立である多変量統計分布を表す.一般的な積分布ProductDistribution[dist1,dist2,…,distn]の確率密度関数(PDF)は厳密に
周辺分布(MarginalDistribution)が厳密に distjであり,成分分布 dist1,dist2,…,distnが独立である多変量統計分布を表す.一般的な積分布ProductDistribution[dist1,dist2,…,distn]の確率密度関数(PDF)は厳密に 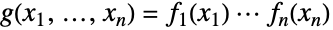 である.ただし,
である.ただし,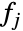 は distjの確率密度関数である.積分布はすべてこの特性を持つが,特定の積分布の特徴と動作はその周辺分布 dist1,dist2,…,distnに依存する.
は distjの確率密度関数である.積分布はすべてこの特性を持つが,特定の積分布の特徴と動作はその周辺分布 dist1,dist2,…,distnに依存する. - 成分分布 dist1,dist2,…,distnは,連続分布でも離散分布でもよく,一変量でも多変量でもよく,標準的な名前付き分布(例:BinomialDistribution,NormalDistribution,HypergeometricDistribution等)のあらゆる組み合せと,それらを(TransformedDistribution,CensoredDistribution,ProductDistribution,CopulaDistribution等によって)変更したものが可能である.さらに,各成分分布 distjは記号分布(例:NormalDistribution[μ,σ])でも数値分布(例:NormalDistribution[0,1])でもよい.短縮形ProductDistribution[{dist1,k1},{dist2,k2},… ,{distn,kn}]を使って第 j 周辺分布 distjが kj回繰り返されることを示すことができる.
- 1940年代に,積分布の系統的な研究を始めるプログラムが提唱された.1950年代から60年代にかけての研究にもかかわらず,このトピックがはじめて徹底的に扱われたのは1966年におけるSpringer and Thompsonの論文であった.それ以来,方法が改善され,特別に定義された(例:区分的)確率分布が理論的にも方法論的にも研究できるようになり,実用的な見地から,積分布が,機械学習や金融等の分野で非常に重要であることが証明された.積分布はモンテカルロ理論やその他の数値メソッドを使っても徹底的に研究されてきた.
- ProductDistributionはその他の分布との間に数多くの関係を持つ.ProductDistributionは,ProductDistribution[dist1,dist2,…,distn]がCopulaDistribution["Product",{dist1,dist2,…,distn}]と等しいという意味で,CopulaDistributionの特殊ケースである.KDistributionはGammaDistributionに従って分布した変数の積であると定義される.LogNormalDistributionの2つの積もまたLogNormalDistributionである.BetaDistributionとGammaDistributionの積はGammaDistributionである.対角共分散行列を持つMultinormalDistribution(したがってBinormalDistribution)は周辺分布がNormalDistributionであるProductDistributionの例である.
例題
すべて開くすべて閉じるスコープ (26)
基本的な用法 (7)
パラメトリック分布 (6)
BinormalDistributionと比較する:
独立PoissonDistributionの積分布を定義する:
MultivariatePoissonDistributionには独立成分はない:
2つの独立StudentTDistributionの例の積分布を作る:
MultivariateTDistributionをフィットする:
MultinormalDistributionの周辺分布を求める:
は対角共分散行列を持つMultinormalDistributionである:
ノンパラメトリック分布 (3)
SmoothKernelDistributionの積分布を定義する:
からサンプルを作り,このサンプルのSmoothKernelDistributionを定義する:
EmpiricalDistributionの積分布を定義する:
HistogramDistributionで積分布を定義する:
派生分布 (10)
CensoredDistributionに従う積分布を定義する:
MarginalDistributionはProductDistributionの成分を選ぶ:
積分布の成分は独立していると考えられるので,![]() が0ではない場合はもとの分布を復元することができない:
が0ではない場合はもとの分布を復元することができない:
MixtureDistributionから積分布を作る:
最大と最小のOrderDistributionの積分布を求める:
ParameterMixtureDistributionの積分布を定義する:
積分布はTransformedDistributionの入力として使われる:
TransformedDistributionの積分布を求める:
TruncatedDistributionの積分布を求める:
TruncatedDistributionの積分布を求める:
QuantityDistributionの積を評価するとQuantityDistributionになる:
アプリケーション (8)
もとの分布は相関していないが,サンプルは若干の相関性を有する:
2人の人間が特定の場所で午後5時から5時半までの間に会おうとしている.各人が,相手とは無関係に,この時間区間内に一様分布に従う時刻に到着し5分間相手を待つとして,2人が会う確率を求める:
2個の六面のサイコロが互いに独立で投げられる.和の密度を求める:
3個のサイコロが互いに独立で投げられた場合の和の密度を求める:
1辺が14の正方形中で,半径7の円の外に値がある確率を求める:
標準正規分布からサイズ100のランダムなサンプルを生成する:
平均のサンプル分布はNormalDistribution[0,1/10]で与えられる:
一枚1ドルで10枚の券を発売する宝くじがある.各宝くじに当りは1枚しか含まれない.5ドルの元手で5種類の宝くじの券を1枚ずつ買った場合に当りくじが含まれる確率を求める:
映画館でチケットを買うための待ち時間とポップコーンを買うための待ち時間は互いに無関係で,両方とも指数分布に従う.チケットを買うための平均待ち時間は10分でポップコーンを買うための平均待ち時間は5分である.チケットとポップコーンを買って席に着くまでの待ち時間が25分より短い場合の確率を求める:
円柱形のローラーベアリングを製造している工場がある.ベリングの直径は平均5cm,標準偏差0.01cmで正規分布に従う.ベアリングの長さは平均7cm,標準偏差0.01cmで正規分布に従う.長さと直径が独立して分布していると仮定して,長さまたは直径が平均から0.02cmより大きく外れている確率求める.
特性と関係 (7)
テキスト
Wolfram Research (2010), ProductDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/ProductDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "ProductDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ProductDistribution.html.
APA
Wolfram Language. (2010). ProductDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ProductDistribution.html